Gọi \(\alpha\) là góc tạo bởi đường thẳng \(y=-12x+3\) và trục Ox.
Khi đó \(tan\left(180-\alpha\right)=\)

Những câu hỏi liên quan
Câu 8:Gọi là góc tạo bởi đường thẳng và trục Ox. Khi đó Câu 9:Gọi là góc tạo bởi đường thẳng và trục Ox. Khi đó Câu 10:Đường thẳng đi qua hai điểm M(0; 1) và N(- 1; 10) tạo với một góc .Khi đó
Đọc tiếp
Câu 8:
Gọi là góc tạo bởi đường thẳng
là góc tạo bởi đường thẳng  và trục Ox. Khi đó
và trục Ox. Khi đó  Câu 9:
Câu 9:
Gọi là góc tạo bởi đường thẳng
là góc tạo bởi đường thẳng  và trục Ox.
và trục Ox.
Khi đó}=$) Câu 10:
Câu 10:
Đường thẳng đi qua hai điểm M(0; 1) và N(- 1; 10) tạo với một góc
một góc  .Khi đó
.Khi đó 
Gọi
Gọi
Khi đó
Đường thẳng đi qua hai điểm M(0; 1) và N(- 1; 10) tạo với
gọi a là góc tạo bởi đường thẳng y=-12x+3 và trục ox khi đó tan\(\left(180độ-a\right)bằng\)
Gọi a1 là góc kề bù với a
Ta có tana1 =12 => a1 = 85
=> a +a1 =180 => 180 -a =a1 =85 độ
KQ: 85 độ 14phut10 giay...
Đúng 0
Bình luận (0)
gọi \(\alpha\) là góc tạo bởi đường thẳng y = -2x - 3 và trục Ox
Khi đó tan \(\alpha\) = ?
gọi a là góc tạo bởi đường thẳng =-6x+ và trục Ox. Khi đó tan(180 độ-a) bằng bao nhiêu
b) Hãy so sánh các hệ số \(a\) của các đường thẳng \(y = ax + b\left( {a \ne 0} \right)\) trong mỗi hình ở Hình 2 và so sánh các góc \(\alpha \) hoặc các góc \(\beta \) tạo bởi các đường thẳng đó với trục \(Ox\).
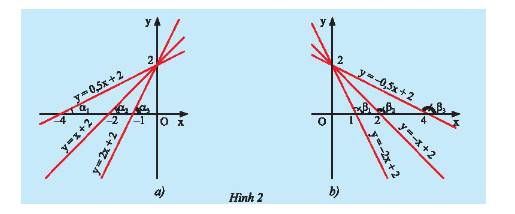
b)
- Ở hình 2a là đồ thị của 3 hàm số \(y = 0,5x + 2;y = x + 2;y = 2x + 2\).
Ta có: \({a_1} = 0,5;{a_2} = 1;{a_3} = 2\) nên \({a_1} < {a_2} < {a_3}\).
Ta có: \({\alpha _1} < {\alpha _2}\) (góc ngoài của tam giác luôn lớn hơn góc trong không kề với nó).
\({\alpha _2} < {\alpha _3}\) (góc ngoài của tam giác luôn lớn hơn góc trong không kề với nó).
Do đó, \({\alpha _1} < {\alpha _2} < {\alpha _3}\).
- Ở hình 2b là đồ thị của 3 hàm số \(y = - 2x + 2;y = - x + 2;y = - 0,5x + 2\).
Ta có: \({a_1} = - 2;{a_2} = - 1;{a_3} = - 0,5\) nên \({a_1} < {a_2} < {a_3}\).
Ta có: \({\beta _1} < {\beta _2}\) (góc ngoài của tam giác luôn lớn hơn góc trong không kề với nó).
\({\beta _2} < {\beta _3}\) (góc ngoài của tam giác luôn lớn hơn góc trong không kề với nó).
Do đó, \({\beta _1} < {\beta _2} < {\beta _3}\).
Đúng 1
Bình luận (0)
gọi \(\alpha\) là góc tạo bởi đường thẳng y=\(-2014\left(x-2014^{2013}\right)+2011^{2012}\)
thì tan(180-\(\alpha\))= bằng bao nhiêu
\(\tan^{-1}\left(-2014\right)=\alpha\)
Đúng 0
Bình luận (0)
-2014 là hệ số góc của đt => Góc tạo bởi đường thẳng tính = CT \(tan^{-1}\left(-2014\right)\)
Ra nhiu lấy 180 - đi
Trừ ra tính Tan ra 2014
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
gọi a là góc tạo bởi đường thẳng y=2x-3 và trục ox khi đó tan a bằng
cậu lúc nào cung '' a '' vậy oOo KiRitO oOo
Đúng 0
Bình luận (0)
Gọi β là góc tạo bởi đường thẳng (d): y = -2016(x - 20152013) + 20142013 và trục Ox.
Khi đó tan(180o - β) = .............
Thì bằng \(-2016\) chứ còn bằng bao nhiêu nữa? Đây là tính chất của hệ số góc mà.
Đúng 0
Bình luận (0)
Cho hình chóp đều S.ABCD có cạnh đáy bằng 2, cạnh bên bằng 2sqrt[]{2} . Gọi alpha là góc tạo bởi hai mặt phẳng left(SACright) và left(SABright). Khi đó cosalpha bằng
Đọc tiếp
Cho hình chóp đều \(S.ABCD\) có cạnh đáy bằng \(2\), cạnh bên bằng \(2\sqrt[]{2}\) . Gọi \(\alpha\) là góc tạo bởi hai mặt phẳng \(\left(SAC\right)\) và \(\left(SAB\right)\). Khi đó \(cos\alpha\) bằng
Lời giải:
Gọi $O$ là tâm đáy thì $SO\perp (ABCD)$
Ta thấy:
$BO\perp AC, BO\perp SO\Rightarrow BO\perp (AC, SO)$
Hay $BO\perp (SAC)(*)$
Gọi $T$ là trung điểm $AB$, $OH\perp ST$.
$OT\perp AB$
$SO\perp AB$
$\Rightarrow (SOT)\perp AB$
$\Rightarrow OH\perp AB$
Mà $OH\perp ST$
$\Rightarrow OH\perp (AB, ST)$ hay $OH\perp (SAB)(**)$
Từ $(*); (**)\Rightarrow \cos a=\cos \widehat{HOB}$
Trong đó:
$BO=\frac{2\sqrt{2}}{2}=\sqrt{2}$
$SO=\sqrt{SB^2-BO^2}=\sqrt{(2\sqrt{2})^2-(\sqrt{2})^2}=\sqrt{6}$
$ST=\sqrt{SO^2+OT^2}=\sqrt{6+1}=\sqrt{7}$
$OH=\frac{SO.OT}{ST}=\frac{\sqrt{6}.1}{\sqrt{7}}=\sqrt{\frac{6}{7}}$
Vì $OH\perp (SAB)$ nên tam giác $BHO$ vuông tại $H$. Do đó:
$\cos a=\cos \widehat{HOB}=\frac{HO}{OB}=\frac{\sqrt{6}}{\sqrt{7}.\sqrt{2}}=\frac{\sqrt{3}}{\sqrt{7}}$
Đúng 1
Bình luận (0)















