Cho tam giác ABC đường cao AH biết AB =15a AC =20a (a>0). Tính độ dài AH

Những câu hỏi liên quan
Cho tam giác ABC vuông tại A đường cao AH biết AB =15a, AC =20a (a>0). Tính dộ dài AH
Áp dụng hệ thức lượng:
\(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\Rightarrow AH=\dfrac{AB.AC}{\sqrt{AB^2+AC^2}}=\dfrac{15a.20a}{\sqrt{\left(15a\right)^2+\left(20a\right)^2}}=12a\)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, đường cao AH, biết AB = 6cm, BC = 10cm
a) Tính độ dài AC.
b) Tính diện tích tam giác ABC.
c) Tính độ dài đường cao AH.
a: AC=8cm
b: \(S_{ABC}=\dfrac{AB\cdot AC}{2}=\dfrac{6\cdot8}{2}=24\left(cm^2\right)\)
c: AH=4,8cm
Đúng 0
Bình luận (1)
cho tam giác góc vuông ABC(A90)có đường cao ah . biết Ab3cm và AC4cm.a chứng minh tam giác HBAcho tam giác góc vuông ABC(A90)có đường cao ah . biết Ab3cm và AC4cm.a chứng minh tam giác HBA~ AbC, B tính độ dài BC và AH AbC, B tính độ dài BC và AH
Đọc tiếp
cho tam giác góc vuông ABC(A=90)có đường cao ah . biết Ab=3cm và AC=4cm.a chứng minh tam giác HBAcho tam giác góc vuông ABC(A=90)có đường cao ah . biết Ab=3cm và AC=4cm.a chứng minh tam giác HBA~ AbC, B tính độ dài BC và AH AbC, B tính độ dài BC và AH
a: Xét ΔHBA vuông tại H và ΔABC vuông tại A có
góc B chung
=>ΔHBA đồng dạng với ΔABC
b: \(BC=\sqrt{3^2+4^2}=5\left(cm\right)\)
AH=3*4/5=2,4cm
Đúng 0
Bình luận (0)
a. Xét ΔHBA và ΔABC có:
\(\widehat{H}=\widehat{A}\) = 900 (gt)
\(\widehat{B}\) chung
\(\Rightarrow\) ΔHBA \(\sim\) ΔABC (g.g)
b. Vì ΔABC vuông tại A
Theo đ/lí Py - ta - go ta có:
BC2 = AB2 + AC2
BC2 = 32 + 42
\(\Rightarrow\) BC2 = 25 cm
\(\Rightarrow\) BC = \(\sqrt{25}=5\) cm
Ta lại có: ΔHBA \(\sim\) ΔABC
\(\dfrac{AH}{CA}=\dfrac{BA}{BC}\)
\(\Leftrightarrow\dfrac{AH}{4}=\dfrac{3}{5}\)
\(\Rightarrow\) AH = 2,4 cm
Đúng 0
Bình luận (0)
1.Cho tam giác ABC vuông tại A , đường phân giác BE , biết EC3cm ,BC6cm . Tính độ dài các đoạn thẳng AB, AC .2.Cho tam giác ABC vuông tại A , đường cao AH . Biết AB:AC3:7 , AH42cm.Tính độ dài BH , CH3.Cho tam giác ABC vuông tại A , đường cao AH . Biết BH:CH9:16 , AH-48cm.Tính độ dài các cạnh góc vuông của tam giác ABC4.Cho tam giác ABC vuông tại A ,phân giác AD , đường cao AH. Biết AB21cm,AC28cm .Tính HD
Đọc tiếp
1.Cho tam giác ABC vuông tại A , đường phân giác BE , biết EC=3cm ,BC=6cm . Tính độ dài các đoạn thẳng AB, AC .
2.Cho tam giác ABC vuông tại A , đường cao AH . Biết AB:AC=3:7 , AH=42cm.Tính độ dài BH , CH
3.Cho tam giác ABC vuông tại A , đường cao AH . Biết BH:CH=9:16 , AH-48cm.Tính độ dài các cạnh góc vuông của tam giác ABC
4.Cho tam giác ABC vuông tại A ,phân giác AD , đường cao AH. Biết AB=21cm,AC=28cm .Tính HD
Cho tam giác ABC vuông tại A, đường cao AH. Biết AB 3cm, AC 4cm. Tính độ dài đường cao AH, tính
c
o
s
A
C
B
^
và chu vi tam giác ABH. A. AH 2,8 cm;
c
o
s
A
C
B
^
3
5
B. AH 2,4 cm; ...
Đọc tiếp
Cho tam giác ABC vuông tại A, đường cao AH. Biết AB = 3cm, AC = 4cm. Tính độ dài đường cao AH, tính c o s A C B ^ và chu vi tam giác ABH.
A. AH = 2,8 cm; c o s A C B ^ = 3 5
B. AH = 2,4 cm; c o s A C B ^ = 4 5
C. AH = 2,5 cm; c o s A C B ^ = 3 4
D. AH = 1,8 cm; c o s A C B ^ = 2 3
Áp dụng định lý Pytago trong ∆ ABC vuông tại A ta có:
![]()
Áp dụng hệ thức lượng trong ∆ ABC vuông tại A có đường cao AH ta có:
![]()
![]()
Đáp án cần chọn là: B
Đúng 2
Bình luận (0)
Cho Tam giác ABC vuông tại A cái đường cao AH
a) Biết AB=6cm, BC=10cm.Hãy tính độ dài các đoạn BH,CH ,AH,AC b)Biết AB = căn 3cm,AC =1cm. Hãy tính độ dài các đoạn BC, AH, BH, CH
c) Biết BH=16a, CH=9a (a>0). Hãy tính độ dài các đoạn AH, BC, AB, AC
d) Biết AB=15a, AC= 20a (a>0). Hãy tính độ dài đoạn thẳng AH
Bài 1:
Áp dụng HTL trong tam giác vuông:
$AB^2=BH.BC$
$\Rightarrow BH=\frac{AB^2}{BC}=\frac{6^2}{10}=3,6$ (cm)
$CH=BC-BH=10-3,6=6,4$ (cm)
Tiếp tục áp dụng HTL:
$AH^2=BH.CH=3,6.6,4$
$\Rightarrow AH=4,8$ (cm)
$AC^2=CH.BC=6,4.10=64$
$\Rightarrow AC=8$ (cm)
Đúng 0
Bình luận (0)
Bài 2:
Áp dụng định lý Pitago:
$BC=\sqrt{AB^2+AC^2}=\sqrt{3^2+1^2}=2$ (cm)
$AH=\frac{2S_{ABC}}{BC}=\frac{AB.AC}{BC}=\frac{\sqrt{3}.1}{2}=\frac{\sqrt{3}}{2}$ (cm)
$BH=\sqrt{AB^2-AH^2}=\sqrt{3-\frac{3}{4}}=\frac{3}{2}$ (cm)
$CH=BC-BH=2-\frac{3}{2}=\frac{1}{2}$ (cm)
Đúng 0
Bình luận (0)
3.
$BC=BH+CH=16a+9a=25a$
Áp dụng HTL trong tam giác vuông:
$AH^2=BH.CH=16a.9a=(12a)^2$
$\Rightarrow AH=12a$ (do $a>0$)
$AB=\sqrt{BH^2+AH^2}=\sqrt{(16a)^2+(12a)^2}=20a$
$AC=\sqrt{CH^2+AH^2}=\sqrt{(9a)^2+(12a)^2}=15a$
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
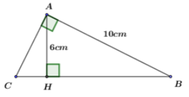
Cho tam giác ABC vuông tại A, đường cao AH. Biết AB = 10cm, AH = 6cm. Tính độ dài các cạnh AC, BC của tam giác ABC.
A. AC = 6,5 (cm); BC = 12 (cm)
B. AC = 7,5 (cm); BC = 12,5 (cm)
C. AC = 8 (cm); BC = 13 (cm)
D. AC = 8,5 (cm); BC = 14,5 (cm)
Áp dụng định lý Pytago trong tam giác ABH vuông tại H. Ta có:
![]()
Trong tam giác vuông ABC vuông tại A có AH là đường cao
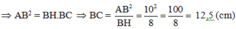
Áp dụng định lý Py-ta-go cho tam giác vuông ABC ta có:
![]()
Vậy AC = 7,5 (cm); BC = 12,5 (cm)
Đáp án cần chọn là: B
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A, AB < AC, đường cao AH. Tính độ dài AB, AC biết AH= 6cm; S tám giác ABC = 37,5 cm2
Đặt AB = x ; AC = y
Sabc = 1/2 BC.AH => BC = 2Sabc / AH = 2.37,5 : 6 = 12,5
Tam giác ABC vuông tại A , theo Py ta go :
AB^2 + AC^2 = BC^2
<=> AB^2 + AC^2 = 12,5^2
=> x^2 + y^2 = 12,5^2
Tam giác ABC vuông tại A , theo HTL :
AB.AC = BC . AH => x.y = 12.5 x 6 = 75
Đến đây tự làm
Đúng 2
Bình luận (0)
Cho tam giác nhọn ABC biết AB=13cm.Kẻ đường cao AH sao cho AH bằng12cm,HC=16cm
a,Tính độ dài AC
b,Tính độ dài BC
Xem chi tiết
Hình tự vẽ! a) Vì AH là đường cao của \(\Delta ABC\Rightarrow\widehat{AHB}=\widehat{AHC}=90^0\)
Xét \(\Delta ABC\) có \(\widehat{AHC}=90^0\Rightarrow AH^2+HC^2=AC^2\) ( ĐL Pytago )
\(\Rightarrow AC^2=12^2+16^2=144+256=400=20^2\Rightarrow AC=20\left(cm\right)\)
b) Xét \(\Delta ABC\) có \(\widehat{AHB}=90^0\Rightarrow AH^2+HB^2=AB^2\) ( ĐL Pytago )
\(\Rightarrow HB^2=AB^2-AH^2=13^2-12^2=169-144=25=5^2\Rightarrow HB=5\left(cm\right)\)
\(BC=HB+HC=16+5=21\left(cm\right)\)


















