Cho các số thực DƯƠNG a; b; c thỏa mãn \(4a+3b+4c=22.\)Tìm GTNN của biểu thức:
\(P=a+b+c+\frac{1}{3a}+\frac{2}{b}+\frac{3}{c}.\)
Cho a là số thực dương khác 1 và x,y là các số thực dương. Mệnh đề nào dưới đây đúng?
A. log a a 3 = 3
B. log a ( x 2 y ) = 2 log a x log a y
C. log a ( xy ) - log a y = log a x
D. log a xlog a y = log a ( xy )
Cho x, y là các số thực dương thỏa mãn log 25 x 2 = log 15 y = log 9 x + y 4 và x y = - a + b 2 với a, b là các số nguyên dương. Tính a + b
A. 14
B. 3
C. 21
D. 32
Đáp án D
Đặt log 25 x 2 = log 15 y = log 9 x + y 4 = t ⇒ x 2 = 25 t y = 15 t x + y = 4 . 9 t
⇒ 2 . 15 t + 15 t = 4 . 9 t x y = 2 5 3 t ⇒ 2 . 5 3 2 t + 5 3 t - 4 = 0 ⇔ [ 5 3 t = - 1 + 33 4 5 3 t = - 1 - 33 4
⇒ 5 3 t = - 1 + 33 4 ⇒ x y = - 1 + 33 4 ⇒ a = - 1 b = 33 ⇒ a + b = 32 .
Cho x, y là các số thực dương thỏa mãn log 25 x 2 = log 15 y = log 9 x + y 4 và x y = − a + b 2 , với a, b là các số nguyên dương. Tính a+b
A. 14
B. 3
C. 21
D. 32
Cho x, y là các số thực dương thỏa mãn log 25 x 2 = log 15 y = log 19 x + y 4 và x y = - a + b 2 với a, b là các số nguyên dương. Tính a + b
A. 14
B. 3
C. 21
D. 34
Cho x, y là các số thực dương thỏa mãn log 25 x 2 = log 15 y = log 9 x + y 4 và x y = - a + b 2 , với a, b là các số nguyên dương. Tính a + b
A. 14
B. 3
C. 21
D. 32
Cho a,b,c,d là các số thực dương
Cho a,b,c là các số thực dương
Chứng minh 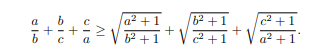
Cho các thực dương a và số thực b khác 0. Mệnh đề nào sau đây là đúng?
A. log 2019 2019 a 3 b 2 = 1 + 1 3 log 2019 a - 2 log 2019 b
B. log 2019 2019 a 3 b 2 = 1 + 3 log 2019 a - 2 log 2019 b
C. log 2019 2019 a 3 b 2 = 1 + 1 3 log 2019 a - 2 log 2019 b
D. log 2019 2019 a 3 b 2 = 1 + 3 log 2019 a - 2 log 2019 b
Cho a,b là các số thực dương, a ≠ 1 . Khi đó a log b c bằng:
A. b a
B. a
C. b
D. a b
Cho x, y là các số thực dương thỏa mãn lnx + lny ≥ ln(x2+y) là các số thực dương thỏa mãn P = x + y
A. P = 6
B. P = 2 + 3 2
C. P = 3 + 2 2
D. P = 17 + 3
Đáp án C
Ta có
![]()

Khi đó

![]()
Vậy giá trị nhỏ nhất của biểu thức P là 3 + 2 2