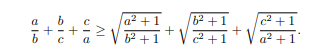Chương 4: BẤT ĐẲNG THỨC, BẤT PHƯƠNG TRÌNH
Các câu hỏi tương tự
3 tháng 2 2021 lúc 15:22
. Cho a, b, c là các số thực dương có tổng bằng 3.
Chứng minh rằng : \(\sqrt{ab+c}+\sqrt{bc+a}+\sqrt{ca+b}\ge3\sqrt{2abc}\)
Với a,b,c là các số thực dương, a + b + c 1, chứng minh rằng:Mình đang cần gấp ạ huhuh
Đọc tiếp
Với a,b,c là các số thực dương, a + b + c = 1, chứng minh rằng:
Mình đang cần gấp ạ huhuh
26 tháng 12 2020 lúc 14:20
Bài 5. Cho là các số thực dương. Chứng minh rằng
Đọc tiếp
Bài 5. Cho 
25 tháng 12 2020 lúc 21:05
Bài 3. Cho là các số thực dương thỏa mãn Chứng minh rằng
Đọc tiếp
Bài 3. Cho 
Cho a,b,c là ba số thực dương. Chứng minh rằng \(\frac{5a+c}{b+c}+\frac{6b}{c+a}+\frac{5c+a}{a+b}\ge9\)
Cho a,b,c,d là các số thực dương
Đọc tiếp
Cho a,b,c,d là các số thực dương
Cho ba số thực dương a, b, c thỏa mãn a+b+c=3. Chứng minh rằng
\(a^3+b^3+c^3+ab+ac+bc\ge6\)
với a,b,c là các số thực dương cho trước. Chứng minh rằng:
\(3a^2+2b^2+5c^2>=c\left(a+b\right)\left(a+c\right)\)
cho các số thực a,b,c dương chứng minh rằng a+b+c≤\(\frac{1}{2}\left(a^2b+b^2c+c^2a+\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\)