a là nghiệm nên \(\sqrt{2}a^2+a-1=0\Rightarrow\sqrt{2}a^2=1-a\)

\(\Rightarrow2a^4=\left(1-a\right)^2=a^2-2a+1\)

\(\Rightarrow2a^4-2a+3=a^2-4a+4=\left(a-2\right)^2\)

Mặt khác \(1-a=\sqrt{2}a^2>0\Rightarrow a< 1\)

\(\Rightarrow\sqrt{2\left(2a^4-2a+3\right)}+2a^2=\sqrt{2\left(a-2\right)^2}+2a^2=\sqrt{2}\left(2-a\right)+2a^2\)

\(=\sqrt{2}\left(\sqrt{2}a^2-a+2\right)=\sqrt{2}\left(1-a-a+2\right)=\sqrt{2}\left(3-2a\right)\)

\(\Rightarrow C=\dfrac{2a-3}{\sqrt{2}\left(3-2a\right)}=-\dfrac{\sqrt{2}}{2}\)

Thay \(\sqrt{2}a^2=1-a\ge\)0 suy ra a <=1 tính được mẫu = \(-\sqrt{2}\left(2a-3\right)\)

ta có :

\(\sqrt{2}a^2+a-1=0\Leftrightarrow\sqrt{2}a^2=1-a\) nên ta có \(a\le1\)

\(\Rightarrow2a^4=a^2-2a+1\)Vậy \(C=\frac{2a-3}{\sqrt{2\left(a^2-4a+4\right)}+2a^2}=\frac{2a-3}{2a^2+\sqrt{2}\left(2-a\right)}=\frac{2a-3}{\sqrt{2}\left(\sqrt{2}a^2-a+2\right)}\)

\(=\frac{2a-3}{\sqrt{2}\left(1-a-a+2\right)}=\frac{2a-3}{\sqrt{2}\left(3-2a\right)}=-\frac{1}{\sqrt{2}}\)

Sửa lại đề bài là giải PT và biện luận nhé các bạn

giúp mình với 

ĐKXĐ: \(x\ne\dfrac{3a}{2}\)

- Với \(a=0\) pt vô nghiệm

- Với \(a\ne0\)

\(\dfrac{2a}{2x-3a}=1\Leftrightarrow2a=2x-3a\)

\(\Leftrightarrow2x=5a\Rightarrow x=\dfrac{5a}{2}\)

Cách 1

Ta có: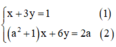 

Từ (1) rút ra được x = 1 – 3y (*)

Thay vào phương trình (2) ta được :

(a2 + 1).(1 – 3y) + 6y = 2a

⇔ a2 + 1 – 3(a2 + 1)y + 6y = 2a

⇔ a2 +1- 2a = 3a2.y – 6y + 3y

⇔ ( a- 1)2 = 3a2y – 3y

⇔ 3(a2 – 1).y = (a – 1)2 (**)

a = 0, phương trình (**) trở thành -3y = 1 ⇔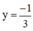 

Thay 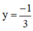 vào (*) ta được x = 2.

Vậy hệ phương trình khi a = 0 có nghiệm duy nhất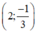 

Thay a = 0 vào hệ phương trình ta được hệ phương trình mới:

a.

\(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\x^2-x+1=x^2\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\1-x=0\end{matrix}\right.\)

\(\Leftrightarrow x=1\)

b.

ĐKXĐ: \(\left[{}\begin{matrix}x\ge2\\x\le-3\end{matrix}\right.\)

Do \(\left\{{}\begin{matrix}\sqrt{x^2-3x+2}\ge0\\\sqrt{x^2+x-6}\ge0\end{matrix}\right.\) với mọi x thuộc TXĐ

\(\Rightarrow\sqrt{x^2-3x+2}+\sqrt{x^2+x-6}\ge0\)

Đẳng thức xảy ra khi:

\(\left\{{}\begin{matrix}x^2-3x+2=0\\x^2+x-6=0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x=1\\x=2\end{matrix}\right.\\\left\{{}\begin{matrix}x=2\\x=-3\end{matrix}\right.\end{matrix}\right.\) \(\Leftrightarrow x=2\) (thỏa mãn ĐKXĐ)

Vậy pt có nghiệm duy nhất \(x=2\)

c.

Với \(x< 1\Rightarrow\left\{{}\begin{matrix}x-1< 0\\\sqrt{x^4-2x^2+1}\ge0\end{matrix}\right.\) phương trình vô nghiệm

Với \(x\ge1\) pt tương đương:

\(\sqrt{\left(x^2-1\right)^2}=x-1\)

\(\Leftrightarrow\left|x^2-1\right|=x-1\)

\(\Leftrightarrow x^2-1=x-1\) (do \(x\ge1\Rightarrow x^2-1\ge0\Rightarrow\left|x^2-1\right|=x-1\))

\(\Leftrightarrow x^2-x=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=0< 1\left(loại\right)\\x=1\end{matrix}\right.\)