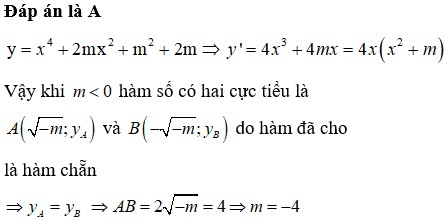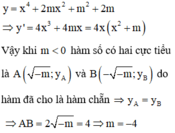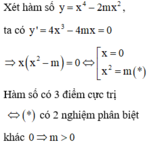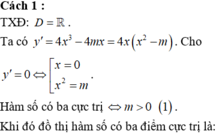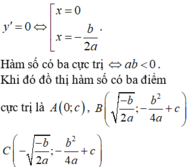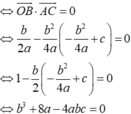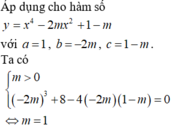Tìm tất cả giá trị của tham số m để đồ thị của hàm y=x4 + 2mx2 + m2 + m có 3 điểm cực trị

Những câu hỏi liên quan
Tìm tất cả các giá trị thực của tham số m để sao cho đồ thị của hàm số y = x 4 + 2 m x 2 + m 2 + 2 m có ba điểm cực trị và khoảng cách giữa hai điểm cực tiểu bằng 4.
A. m=-4
B. m=5
C. m=1
C. m=3
Tìm tất cả các giá trị thực của tham số m để sao cho đồ thị của hàm số
y
x
4
+
2
mx
2
+
m
2
+
2
m
có ba điểm cực trị và khoảng cách giữa hai điểm cực tiểu bằng 4. A. m -4 B. m 5 C.
m
1
2
D. m 3
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để sao cho đồ thị của hàm số y = x 4 + 2 mx 2 + m 2 + 2 m có ba điểm cực trị và khoảng cách giữa hai điểm cực tiểu bằng 4.
A. m = -4
B. m = 5
C. m = 1 2
D. m = 3
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số
y
x
4
−
2
m
x
2
+
m
2
−
5
m
có ba điểm cực trị tạo thành một tam giác có diện tích nhỏ hơn
4
2
.
A.
0
m
2
2
B.
m...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y = x 4 − 2 m x 2 + m 2 − 5 m có ba điểm cực trị tạo thành một tam giác có diện tích nhỏ hơn 4 2 .
A. 0 < m < 2 2
B. m > 0
C. 0 < m < 2
D. 2 < m < 2 2
Đáp án C
Có y ' = 4 x 3 − 4 m x ; y ' = 0 ⇔ x = 0 x = m x = − m (ta xét với m > 0 để phương trình có 3 nghiệm)
Khi đó 3 điểm cực trị của hàm số là A 0 ; m 2 − 5 m ; B m ; − 5 m ; C − m ; 5 m .
Khi đó ABC là tam giác cân có đường cao A H = m 2 ; B C = 2 m
S A B C = 1 2 A H . B C = m 2 m < 4 2 ⇔ 0 < m < 2
Đúng 0
Bình luận (0)
Giá trị của tham số m để đồ thị hàm số
y
x
4
+
2
m
x
2
+
m
2
+
m
có 3 điểm cực trị là: A. m0 B. m0 C. m0 D.
m
≠
0
Đọc tiếp
Giá trị của tham số m để đồ thị hàm số y = x 4 + 2 m x 2 + m 2 + m có 3 điểm cực trị là:
A. m=0
B. m>0
C. m<0
D. m ≠ 0
Đáp án C
Hàm số có 3 điểm cực trị khi a b < 0 ⇔ m < 0
Đúng 0
Bình luận (0)
Tìm tất cả giá trị thực của tham số m để đồ thị hàm số
y
x
4
−
2
m
x
2
+
2
m
−
3
có ba điểm cực trị là ba đỉnh của tam giác cân. A.
m
≥
0.
B.
m
0.
C.
m
≠
0
....
Đọc tiếp
Tìm tất cả giá trị thực của tham số m để đồ thị hàm số y = x 4 − 2 m x 2 + 2 m − 3 có ba điểm cực trị là ba đỉnh của tam giác cân.
A. m ≥ 0.
B. m > 0.
C. m ≠ 0 .
D. m < 0.
Đáp án là B
TXĐ D= ℝ
Cách 1.
Ta có: y ' = 4 x 3 − 4 m x = 4 x x 2 − m
Do hàm số đã cho là hàm số trùng phương nên để đồ thị hàm số y = x 4 − 2 m x 2 + 2 m − 3 có ba điểm cực trị là ba đỉnh của một tam giác cân thì phương trình y ¢= 0 phải có 3 nghiệm thực phân biệt.
Û x 2 = m có hai nghiệm phân biệt x ¹ 0 Û m > 0 .
Cách 2. (Dùng cho trắc nghiệm)
Do hàm số đã cho là hàm số trùng phương nên để đồ thị hàm số y = x 4 − 2 m x 2 + 2 m − 3 có ba điểm cực trị là ba đỉnh của một tam giác cân thì a . b < 0 ⇔ 1. − 2 m < 0 ⇔ m > 0.
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị thực của tham số m để đồ thị của hàm số
y
x
4
-
2
m
x
2
có ba điểm cực trị tạo thành một tam giác có diện tích nhỏ hơn 1. A. m 0 B. m 1 C.
0
m
4
3
D. 0 m 1
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để đồ thị của hàm số y = x 4 - 2 m x 2 có ba điểm cực trị tạo thành một tam giác có diện tích nhỏ hơn 1.
A. m> 0
B. m< 1
C. 0 < m < 4 3
D. 0< m< 1
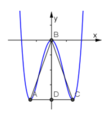
+ Điều kiện để hàm số có 3 cực trị là m> 0
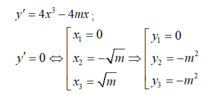
+ Các điểm cực trị tạo thành tam giác cân có đáy bằng 2√m, đường cao bằng m2. (như hình bên )
Ta được S ∆ A B C = 1 2 A C . B D = m . m 2 .
+ Để tam giác có diện tích nhỏ hơn 1 thì m . m 2 < 1 h a y 0 < m < 1
Chọn D.
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị thực của tham số m để đồ thị của hàm số
y
x
4
-
2
m
x
2
có ba điểm cực trị tạo thành một tam giác có diện tích nhỏ hơn 1. A. 0 m 1 B.
0
m
4
3
C. m 1 D. m 0
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để đồ thị của hàm số y = x 4 - 2 m x 2 có ba điểm cực trị tạo thành một tam giác có diện tích nhỏ hơn 1.
A. 0 < m < 1
B. 0 < m < 4 3
C. m < 1
D. m > 0
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số
y
x
4
−
2
m
x
2
có ba điểm cực trị tạo thành một tam giác có diện tích nhỏ hơn 1. A. m1 B.
0
m
4
3
C. m0 D.
0
m
1
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y = x 4 − 2 m x 2 có ba điểm cực trị tạo thành một tam giác có diện tích nhỏ hơn 1.
A. m<1
B. 0 < m < 4 3
C. m>0
D. 0 < m < 1
Đáp án D
Ta có y ' = 4 x 3 − 4 m x = 4 x x 2 − m .
Hàm số có 3 điểm cực trị ⇔ y ' = 0 có 3 nghiệm phân biệt, suy ra m > 0 1 .
Suy ra tọa độ 3 điểm cực trị của đồ thị hàm số là
A 0 ; 0 , B m ; − m 2 , C − m ; − m 2 ⇒ A B ¯ = m ; − m 2 A C ¯ = − m ; − m 2 B C ¯ = 2 m ; 0 .
Suy ra tam giác ABC cân tại A.
Gọi H 0 ; − m 2 là trung điểm của B C ⇒ A H ¯ = 0 ; − m 2 ⇒ A H = m 2 .
Suy ra S A B C = 1 2 A H . B C = 1 2 m 2 2 m 2 = m 4 < 1 ⇔ − 1 < m < 1 2 .
Từ (1), (2) ⇒ 0 < m < 1.
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị của tham số m sao cho đồ thị hàm số
y
-
x
4
+
2
m
x
2
-
2
m
có 3 điểm cực trị tạo tam giác có diện tích bằng 1 A.
m
3
B.
m
1
4
5
C.
m
1
D. ...
Đọc tiếp
Tìm tất cả các giá trị của tham số m sao cho đồ thị hàm số y = - x 4 + 2 m x 2 - 2 m có 3 điểm cực trị tạo tam giác có diện tích bằng 1
A. m = 3
B. m = 1 4 5
C. m = 1
D. m = - 1
Cho hàm số
y
x
4
-
2
m
x
2
+
1
-
m
. Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số có ba điểm cực trị tạo thành một tam giác nhận gốc tọa độ O làm trực tâm. A. m 1 B. m 2 C. m 0 D. m -1
Đọc tiếp
Cho hàm số y = x 4 - 2 m x 2 + 1 - m . Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số có ba điểm cực trị tạo thành một tam giác nhận gốc tọa độ O làm trực tâm.
A. m = 1
B. m = 2
C. m = 0
D. m = -1