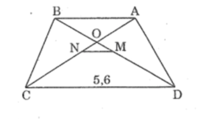
Cho hình thang cân ABCD(AB//CD) có hai đường chéo AC và BD cắt nhau tại O. Gọi M,N theo thứ tự là trung điểm của BD và AC. Cho biết MD=3MO, đáy lớn CD=5,6cm.
a, TÍnh độ dài đoạn thẳng Mn và đáy nhỏ Ab
b, So sánh độ dài đoạn MN với nửa hiệu các dộ dài của CD và AB





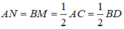
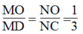
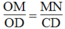 Hệ quả định lí Ta-lét)
Hệ quả định lí Ta-lét)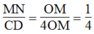
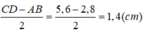














![[ChiIkỎ Ckan]](https://hoc24.vn/images/avt/avt33539123_256by256.jpg)


