Lời giải
a)
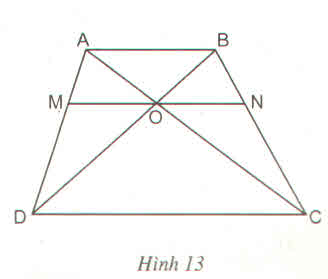
Ta có \(\left\{{}\begin{matrix}MD=MB\\NA=NC\end{matrix}\right.\) \(\Rightarrow\)MN//DC
\(\Rightarrow\Delta OMN\approx\Delta ODC\approx OBA\)
Tỷ số đồng dạng
\(\dfrac{OM}{OD}=\dfrac{MN}{DC}=\dfrac{ON}{OC}\)\(\Rightarrow MN=\dfrac{OM}{OD}.DC=\dfrac{1}{4}.5,6=1,4\left(cm\right)\)
\(\dfrac{OM}{OB}=\dfrac{MN}{AB}\Rightarrow AB=\dfrac{OB}{OM}.MN=2MN=2,8\left(cm\right)\)
b)
\(\left\{{}\begin{matrix}CD=4MN\\AB=2MN\end{matrix}\right.\)
\(\Rightarrow\dfrac{CD-AB}{2}=\dfrac{4MN-2MN}{2}=MN\)











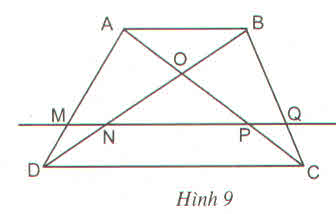 DN\BD=CP\AC
DN\BD=CP\AC