Ta có M, N lần lượt là trung điểm của AB, AD nên MN là đường trung bình của ∆ABD => MN // BD

Mà AC⊥BD nên MN⊥AC hay LA⊥MN (1)

N, L lần lượt là trung điểm của AD, AC nên NL là đường trung bình của ∆ADC => NL // DC

Mà MH⊥DC nên NL⊥MH  (2)

Từ (1) và (2) suy ra H là trực tâm của tam giác MNL (đpcm)

tgiác ABC có MN là đường trung bình => MN // AC và MN = AC/2
tgiác DAC có PQ là đường trung bình => PQ // AC và PQ = AC/2
vậy: MN // PQ và MN = PQ => MNPQ là hình bình hành

mặt khác xét tương tự cho hai tgiác ABD và CBD ta cũng có:
NP // BD và NP = BD/2
do giả thiết AC_|_BD => AC_|_NP mà MN // AC => MN_|_NP

tóm lại MNPQ là hình chữ nhật (hbh có một góc vuông)

b) MNPQ là hình vuông <=> MN = NP <=> AC/2 = BD/2 <=> AC = BD
vậy điều kiện là: tứ giác ABCD có hai đường chéo vuông góc và bằng nhau
c, Vỳ Mn là đườq trung bình của tam giác ABC nên MN= \(\frac{1}{2}\) AC= 3cm

QM là đường trung bình của tam giác ABD nên QM = \(\frac{1}{2}\) BD = 4cm

Mà MNPQ là hình chữ nhật nên diện tích ABCD = ( MN+PQ).2= (3.4):2 = 6cm

giống bài của mình

Xét ΔABD có

M,Q lần lượt là trung điểm của AB,AD

=>MQ là đường trung bình của ΔABD

=>MQ//BD và MQ=BD/2(1)

Xét ΔCBD có

N,P lần lượt là trung điểm của CB,CD

=>NP là đường trung bình của ΔCBD

=>NP//BD và NP=BD/2(2)

Từ (1) và (2) suy ra MQ//NP và MQ=NP

Xét ΔBAC có

M,N lần lượt là trung điểm của BA,BC

=>MN là đường trung bình

=>MN//AC

MN//AC

AC\(\perp\)BD

Do đó: MN\(\perp\)BD

MN\(\perp\)BD

MQ//BD

Do đó: MN\(\perp\)MQ

Xét tứ giác MNPQ có

MQ//NP

MQ=NP

Do đó: MNPQ là hình bình hành

Hình bình hành MNPQ có \(\widehat{NMQ}=90^0\)

nên MNPQ là hình chữ nhật

=>M,N,P,Q cùng nằm trên 1 đường tròn

khó waaaaaaaaaaaaaaaaa

bài zì mà khó quá đi àaaaaaaaaaaaaaaaa

sao không ai giúp tớ

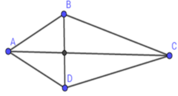
Vì ABCD có đường chéo vuông góc nên

S_ABCD = 1 2 BD. AC

=> AC = 2 S A B C D B D = 2.56 7 = 16 cm.

Đáp án cần chọn là: D

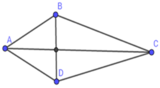
S_ABCD = 1 2 BD. AC

=> AC = 2 S A B C D B D  = 2.25 5  = 10 cm.

Đáp án cần chọn là: A