a: Xét ΔADB và ΔAEC có 

AB=AC

\(\widehat{ABD}=\widehat{ACE}\)

BD=CE

Do đó: ΔADB=ΔAEC

Suy ra: AD=AE

hay ΔADE cân tại A

a)

Chứng minh được tam giác ABD =  tam giác ACE (c-g-c) => AD = AE

Từ đó tam giác ADE cân tại A.

Lời giải:

a) Xét tam giác $AHB$ và $AHC$ có:

$AH$ chung

$AB=AC$ do $ABC$ cân tại $A$

$\widehat{AHB}=\widehat{AHC}=90^0$

$\Rightarrow \triangle AHB=\triangle AHC$ (ch-cgv)

b) 

Vì $ABC$ cân tại $A$ nên $\widehat{ABC}=\widehat{ACB}$

$\Rightarrow 180^0-\widehat{ABC}=180^0-\widehat{ACB}$ 

hay $\widehat{ABD}=\widehat{ACE}$ 

Xét tam giác $ABD$ và $ACE$ có:

$BD=CE$

$AB=AC$

$\widehat{ABD}=\widehat{ACE}$ (cmt)

$\Rightarrow \triangle ABD=\triangle ACE$ (c.g.c)

$\Rightarrow AD=AE$ nên $ADE$ là tam giác cân.

Hình vẽ:

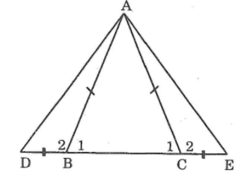
*) Ta có: ΔABC cân tại A

BD = CE (giả thiết)

Suy ra: ΔABD = ΔACE (c.g.c)

⇒ AD = AE ( hai cạnh tương ứng)

*) Tam giác ADE có AD = AE nên tam giác này cân tại A (theo định nghĩa tam giác cân)

nhờ bạn nào đó vẽ hình cho nha, tui ko bt vẽ.

giải 

tam giác ABC cân tại A \(\Rightarrow\)  góc ABC = góc ACB = \(\dfrac{180^o-50^o}{2}=75^o\)

❆góc ABC = \(75^o\)  \(\Rightarrow\)  góc DBA = \(180^o-75^o=105^o\)

\(\Delta DAB\)  có DB=BA  \(\Rightarrow\)  \(\Delta\) DBA cân tại B

                                \(\Rightarrow\)  góc DAB = góc ADB = \(\dfrac{180^o-105^o}{2}=32,5^o\)

❆ góc ACB = \(75^o\)  \(\Rightarrow\)  góc ACE = \(180^o-75^o=105^o\)

     \(\Delta ACE\)   có AC=CE \(\Rightarrow\)   tam giác ACE cân tại C

                                      \(\Rightarrow\)  góc CAE = góc CEA = \(\dfrac{180^o-105^o}{2}=32,5^o\)

❆ ta có : góc DAE = góc DAB + góc CAE + góc BAC 

                              = \(32,5^o+32,5^o+50^o=125^o\)

vậy góc DAE = \(125^o\)

Bạn tự vẽ hình nha!

a.

Ta có:

mà B1 = C1 (tam giác ABC cân tại A)

=> B2 = C2 (1)

Xét tam giác ADB và tam giác AEC:

AB = AC (tam giác ABC cân tại A)

B2 = C2 (theo 1)

BD = CE (gt)

=> Tam giác ADB = ACE (c.g.c)

=> AD = AE (2 cạnh tương ứng)

=> Tam giác ADE

b.

Xét tam giác AHB vuông tại A và tam giác AKC vuông tại K:

 AB = AC (tam giác ABC cân tại A)

A1 = A2 (tam giác ADB = tam giác AEC)

=> Tam giác AHB = Tam giác AKC (cạnh huyền - góc nhọn)

=> BH = CK (2 cạnh tương ứng)

     AH = AK (2 cạnh tương ứng)

c.

Xét tam giác HDB vuông tại H và tam giác KEC vuông tại K:

BH = CK (theo câu b)

BD = CE (gt)

=> Tam giác HDB = Tam giác KEC (cạnh huyền - cạnh góc vuông)

Ta có: 

DBH = IBC (2 góc đối đỉnh)

KCE = ICB (2 góc đối đỉnh)

mà DBH = KCE (tam giác HDB = tam giác KEC)

=> IBC = ICB 

=> Tam giác IBC cân tại I

Bài 5:

Tgiac ABC vuông cân tại A => góc CBA = 45 độ

Xét góc CBA là góc ngoài tgiac DBC => góc CBA = góc D + DCB

Xét tgiac DBC có DB = BC => tgiac DBC cân tại B => góc D = góc DBC

=> góc D = 45/2 = 22,5 độ

và góc ACD = 22,5 + 45 = 67,5 độ

Vậy số đo các góc của tgiac ACD là ...

Bài 6: 

Tgiac ABC cân tại B, góc B = 100 độ => góc A = góc C = 40 độ

Xét tgiac ABD có AB = AD => tgiac ABD cân tại A => góc EDB (ADB) = (180-40)/2 =70 độ

cmtt với tgiac CBE => góc DEB = 70 độ

=> góc DBE = 180-70-70 = 40 độ

Bài 7: 

Xét tgiac ABC cân tại A => góc BAC = 180 - 2.góc C => 2.(90 - góc C)

Xét tgiac BHC vuông tại H => góc CBH = 90 - góc C

=> đpcm

Bài 8: mai làm hihi

bài này dễ sao không biết

Bài 8 :
Tự vẽ hình nhé ?
a) Vì ∆ABC cân tại A (GT)
=> ∠ABC = ∠ACB (ĐN)
Mà ∠ABC + ∠DBC = 180^o (2 góc kề bù)
      ∠ACB + ∠ECB = 180^o (2 góc kề bù)
=> ∠DBC = ∠ECB (1)
Xét ∆BCD và ∆CBE có :
BD = CE (GT)
∠DBC = ∠ECB (Theo (1))
BC chung
=> ∆BCD = ∆CBE (c.g.c) (2)
=> ∠BCD = ∠CBE (2 góc tương ứng)
Hay ∠BCI = ∠CBI
Xét ∆IBC có : ∠BCI = ∠CBI (cmt)
=> ∆IBC cân tại I (định lý)
=> IB = IC (ĐN) (3)
Từ (2) => DC = EB (2 cạnh tương ứng)
Mà ID + IC = DC, IE + IB = EB
=> ID = IE
Xét ∆IDE có : ID = IE (cmt)
=> ∆IDE cân tại I (ĐN)
b) Ta có : AB + BD = AD
    Mà AC + CE = AE
          AB = AC (GT)
          BD = CE (GT)
=> AD = AE 
Xét ∆ADE có : AD = AE (cmt)
=> ∆ADE cân tại A (ĐN)
=> ∠ADE = \(\frac{180^o-\widehat{DAE}}{2}\)(4)
Vì ∆ABC cân tại A (GT)
=> ∠ABC = \(\frac{180^o-\widehat{BAC}}{2}\)(5)
Từ (4), (5) => ∠ADE = ∠ABC, mà 2 góc này ở vị trí đồng vị
=> BC // DE (DHNB)
c) Xét ∆ABM và ∆ACM có :
AM chung
AB = AC (GT)
MB = MC (do M là trung điểm của BC)
=> ∆ABM = ∆ACM (c.c.c)
=> ∠AMB = ∠AMC (2 góc tương ứng)
Mà ∠AMB + ∠AMC = 180^o (2 góc kề bù)
=> ∠AMB = ∠AMC = 180^o : 2 = 90^o 
Sau đó chứng minh ∆BIM = ∆CIM theo c.c.c bằng 3 yếu tố MI chung, MB = MC, IB = IC (Theo (3))
Rồi => ∠IMB = ∠IMC (tương ứng)
Mà ∠IMB + ∠IMC = 180^o (kề bù) 
=> ..... (làm như phần trên)
Ta có : ∠AMB + ∠IMB = ∠AMI
Mà ∠AMB = 90^o (cmt)
      ∠IMB = 90^o (cmt)
=> 90^o + 90^o = ∠AMI
=> ∠AMI = 180^o
=> A, M, I thẳng hàng (đpcm)
Vậy .....

a: Xét ΔABM và ΔACM có

AB=AC

\(\widehat{BAM}=\widehat{CAM}\)

AM chung

Do đó: ΔABM=ΔACM

b: ta có: ΔAMB=ΔAMC

=>\(\widehat{AMB}=\widehat{AMC}\)

mà \(\widehat{AMB}+\widehat{AMC}=180^0\)(hai góc kề bù)

nên \(\widehat{AMB}=\widehat{AMC}=\dfrac{180^0}{2}=90^0\)

=>AM\(\perp\)BC

c: Ta có: \(\widehat{ABC}+\widehat{ABD}=180^0\)(hai góc kề bù)

\(\widehat{ACB}+\widehat{ACE}=180^0\)(hai góc kề bù)

mà \(\widehat{ABC}=\widehat{ACB}\)

nên \(\widehat{ABD}=\widehat{ACE}\)

Xét ΔABD và ΔACE có

AB=AC

\(\widehat{ABD}=\widehat{ACE}\)

BD=CE

Do đó: ΔABD=ΔACE

=>\(\widehat{ADB}=\widehat{AEC}\)

=>\(\widehat{ADC}=\widehat{AEB}\)

Ta thấy AB = BD (GT) ; AC=CE (GT)

Mà AB = AC ( do tam  gaics ABC cân tại A)

Nên BD=CE

Ta thấy ^DBA = 180 dộ - ^ABC

           ^ECA = 180 độ - ^ACB

mà ^ABC = ^ ACB suy ra ^DBA = ^ ECA

Xét tam giác ABD và tam giác ACE có: 

              AB = AC

               ^BDA = ^ECA (cmt)

             BD = CE ( cmt )

suy ra tam giác ABD = tam giác ACE (c.g.c)

Suy ra ^D = ^ E ( 2 cạnh tương ứng)

Suy ra tam giac ADE cân tại A

+, ta thấy DE = BD + BC + CE

MÀ BD =AB ( GT ); CE= AC (GT)

Suy ra DE = AB+ BC+AC

b, Tam giác ABC có: ^BAC + ^ABC+^ACB = 180

                              32 + ^ABC + ^ ACB =180

                               ^ABC + ^ACB = 180-32=158

Suy ra ^ABC = ^ ACB = 158 :2 = 79

Mà ^ABC là góc ngoài của tam giac ABD cân tại b

Nên ^D=79:2=39,5

Suy ra D =^E= 39,5( tam giác ADE cân)

SUY ra DAC= 180-39,5-39,5=101