Cho a // b, \(M_1-N_1=35^o\). Tính \(M_2;N_2\). ( giúp mình với, mình cần gấp lắm )

Những câu hỏi liên quan
Quan sát hình 44, biết a // b.a) So sánh widehat {{M_1}} và widehat {{N_3}}; widehat {{M_4}} và widehat {{N_2}} ( mỗi cặp góc M1 và N3, M4 và N2 gọi là một cặp góc so le ngoài)b) Tính: widehat {{M_2}} + widehat {{N_1}} và widehat {{M_3}} + widehat {{N_4}} ( mỗi cặp góc M2 và N1, M3 và N4 gọi là một cặp góc trong cùng phía)
Đọc tiếp
Quan sát hình 44, biết a // b.
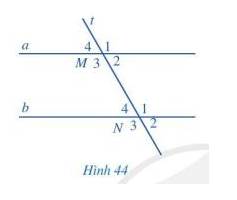
a) So sánh \(\widehat {{M_1}}\) và \(\widehat {{N_3}}\); \(\widehat {{M_4}}\) và \(\widehat {{N_2}}\) ( mỗi cặp góc M1 và N3, M4 và N2 gọi là một cặp góc so le ngoài)
b) Tính: \(\widehat {{M_2}} + \widehat {{N_1}}\) và \(\widehat {{M_3}} + \widehat {{N_4}}\) ( mỗi cặp góc M2 và N1, M3 và N4 gọi là một cặp góc trong cùng phía)
a) Vì a // b nên \(\widehat {{M_1}} = \widehat {{N_1}}\); \(\widehat {{M_4}} = \widehat {{N_4}}\) ( 2 góc đồng vị) mà \(\widehat {{N_3}} = \widehat {{N_1}}\) ; \(\widehat {{N_4}} = \widehat {{N_2}}\) ( 2 góc đối đỉnh) nên \(\widehat {{M_1}}\) =\(\widehat {{N_3}}\); \(\widehat {{M_4}}\) =\(\widehat {{N_2}}\)
b) Vì a // b nên \(\widehat {{M_2}} = \widehat {{N_2}};\widehat {{M_3}} = \widehat {{N_3}}\) ( 2 góc đồng vị), mà \(\widehat {{N_1}} + \widehat {{N_2}} = 180^\circ ;\widehat {{N_3}} + \widehat {{N_4}} = 180^\circ \) ( 2 góc kề bù) nên \(\widehat {{M_2}} + \widehat {{N_1}}\) = 180\(^\circ \); \(\widehat {{M_3}} + \widehat {{N_4}}\)= 180\(^\circ \)
Chú ý:
Nếu đường thẳng c cắt cả hai đường thẳng song song a và b thì:
+ Hai góc so le ngoài bằng nhau
+ Hai góc trong cùng phía có tổng số đo bằng 180\(^\circ \)
Đúng 0
Bình luận (0)
Cho M_130^O;N_150^O;MON80^O. Chứng tỏ a // b a b O M N 1 1
Đọc tiếp
Cho \(M_1=30^O;N_1=50^O;MON=80^O\). Chứng tỏ a // b
Kẻ Oz//a
\(\Rightarrow\widehat{M_1}=\widehat{MOz}=30^0\)(so le trong)
\(\Rightarrow\widehat{NOz}=\widehat{MON}-\widehat{MOz}=80^0-30^0=50^0\)
\(\Rightarrow\widehat{NOz}=\widehat{N_1}=50^0\)
Mà 2 góc này so le trong
=> Oz//b
=> a//b
Đúng 2
Bình luận (1)
Bài 4:Cho hình vẽ, biết aperpMP tại M, bperp NQ tại Q, widehat{N_1}65^O.a) Chứng tỏ a//b.b) Tính widehat{M_1}? M P Q a b 1 1 65 độ N
Đọc tiếp
Bài 4:Cho hình vẽ, biết a\(\perp\)MP tại M, \(b\perp NQ\) tại Q, \(\widehat{N_1}\)=\(65^O\).
a) Chứng tỏ a//b.
b) Tính \(\widehat{M_1}\)=?
ta có : a \(\perp\) P và b \(\perp\) Q \(\Rightarrow\)a//b
M1 và N1 là cặp góc trong cùng phía bù nhau
\(\Rightarrow\)M1= \(^{180^0}\)- N1= 180- \(65^0\)= 115
Đúng 0
Bình luận (0)
Câu 1: Hai vật có khối lượng m_1và m_2left(m_1m_2right) chuyển động cùng vận tốc. So sánh động năng của hai vật:
A. bằng nhau
B. động năng của vật có khối lượng m_2 lớn hơn
C. động năng của vật có khối lượng m_1 lớn hơn
D. cả A, B, C đều sai
Câu 2: Hai vật có khối lượng m_1và m_2left(m_1m_2right) ở cùng độ cao so với mặt đất. So sánh thế năng của hai vật:
A. bằng nhau
B. thế năng của vật có khối lượng m_2 lớn hơn
C. thế năng của vật có khối lượng m_1 lớn hơn
D. cả A, B, C đều sai
Câu 2...
Đọc tiếp
Câu 1: Hai vật có khối lượng \(m_1\)và \(m_2\left(m_1>m_2\right)\) chuyển động cùng vận tốc. So sánh động năng của hai vật:
A. bằng nhau
B. động năng của vật có khối lượng \(m_2\) lớn hơn
C. động năng của vật có khối lượng \(m_1\) lớn hơn
D. cả A, B, C đều sai
Câu 2: Hai vật có khối lượng \(m_1\)và \(m_2\left(m_1>m_2\right)\) ở cùng độ cao so với mặt đất. So sánh thế năng của hai vật:
A. bằng nhau
B. thế năng của vật có khối lượng \(m_2\) lớn hơn
C. thế năng của vật có khối lượng \(m_1\) lớn hơn
D. cả A, B, C đều sai
Câu 2: Hai vật có khối lượng \(m_1\)và \(m_2\left(m_1>m_2\right)\) chuyển động có động năng bằng nhau. So sánh vận tốc của hai vật:
A. bằng nhau
B. vận tốc của vật có khối lượng \(m_2\) lớn hơn
C. vận tốc của vật có khối lượng \(m_1\) lớn hơn
D. cả A, B, C đều sai
1. C
\(W_đ=\frac{1}{2}mv^2\)
2. C
\(W_t=mgh\)
3. B
\(W_đ=\frac{1}{2}mv^2\)
\(W_{đ1}=W_{đ2}\Rightarrow\frac{1}{2}m_1v_1^2=\frac{1}{2}m_2v_2^2\Rightarrow\frac{v_2}{v_1}=\sqrt[]{\frac{m_1}{m_2}}\)
Đốt cháy hoàn toàn \(m_1\) gam R trong \(m_2\) gam oxi thu đc hỗn hợp khí gồm RO2 và O2 có tỉ khối so với H2 là 25,6. Hãy tính tỉ lệ \(\dfrac{m_1}{m_2}\)
Gọi số mol R, O2 là a, b (mol)
=> m1 = a.MR; m2 = 32b
PTHH: R + O2 --to--> RO2
a->a-------->a
=> hh khí gồm \(\left\{{}\begin{matrix}RO_2:a\left(mol\right)\\O_{2\left(dư\right)}:b-a\left(mol\right)\end{matrix}\right.\)
Xét \(\overline{M}=\dfrac{a\left(M_R+32\right)+32\left(b-a\right)}{a+\left(b-a\right)}=25,6.2=51,2\)
=> a.MR = 19,2b
Xét \(\dfrac{m_1}{m_2}=\dfrac{a.M_R}{32b}=\dfrac{19,2b}{32b}=\dfrac{3}{5}\)
Đúng 1
Bình luận (0)
Một khung cửa sổ hình tam giác có thiết kế như Hình 18a được vẽ lại như Hình 18b.
a) Cho biết \(\widehat {{A_1}}\)\( = {42^o}\). Tính số đo của \(\widehat {{M_1}}\),\(\widehat {{B_1}}\),\(\widehat {{M_2}}\).
b) Chứng minh MN // BC, MP // AC.
c) Chứng minh bốn tam giác cân AMN, MBP, PMN, NPC bằng nhau.
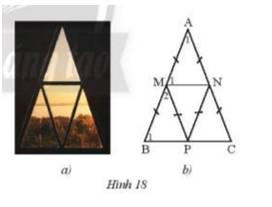
a) Ta thấy tam giác AMN cân tại A do AM = AN
\( \Rightarrow \widehat {{M_1}} = ({180^o} - \widehat {{A_1}}):2 = ({180^o} - {42^o}):2 = {69^o}\)
Ta thấy tam giác PMN = tam giác AMN ( c-c-c )
\( \Rightarrow \widehat {{M_1}} = \widehat {PMN} = {69^o}\) (góc tương ứng )
Mà \( \Rightarrow \widehat {{M_1}} + \widehat {{M_2}} + \widehat {PMN} = {180^o}\)( các góc kề bù )
\( \Rightarrow \widehat {{M_2}} = {180^o} - {69^o} - {69^o} = {42^o}\)
Mà tam giác MPB cân tại M do MB = MP nên
\( \Rightarrow \widehat {{B_1}} = \widehat {MPB}\)
Áp dụng định lí tổng 3 góc trong tam giác
\( \Rightarrow \widehat {{B_1}} = ({180^o} - {42^o}):2 = {69^o}\)
b) Ta thấy \(\widehat {{B_1}}\)và \(\widehat {{M_1}}\)ở vị trí đồng vị và bằng nhau nên
\( \Rightarrow \)MN⫽BC
Vì tam giác PMN = tam giác AMN nên ta có
\( \Rightarrow \widehat {{M_1}} = \widehat {ANM} = \widehat {PMN} = \widehat {MNP}\)( do 2 tam giác cân và bằng nhau )
Mà \(\widehat {MNA}\)và\(\widehat {PMN}\) ở vị trí so le trong
\( \Rightarrow \)MP⫽AC
c) Ta có \(\Delta AMN = \Delta PMN = \Delta MBP(c - g - c)\)(1)
Vì MP⫽AC ( chứng minh trên )
\( \Rightarrow \widehat {MPN} = \widehat {PNC}\) ( 2 góc so le trong ) =\({42^o}\)
\( \Rightarrow \Delta MPN = \Delta NCP(c - g - c)\)(2)
Từ (1) và (2) \( \Rightarrow \) 4 tam giác cân AMN, MBP, PMN, NCP bằng nhau
Đúng 0
Bình luận (0)
Cho con lắc lò xo lí tưởng có độ cứng k100Nm^{-1}. Ba vật có khối lượng lần lượt là m_0dfrac{1}{12}kg,m_1200g,m_250g. Bỏ qua lực cản không khí, lực ma sát giữa m_1,m_0 và mặt sàn. Cho hệ số ma sát giữa m_1,m_2 là mu0,6. Lấy g10ms^{-2}. Vật m_0 phải có vận tốc đầu v_0 thỏa mãn điều kiện gì để giữa hai vật m_1,m_2 không xảy ra sự trượt trong quá trình dao động?
Đọc tiếp
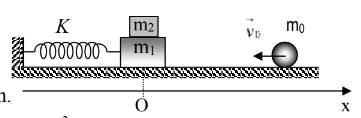
Cho con lắc lò xo lí tưởng có độ cứng \(k=100Nm^{-1}\). Ba vật có khối lượng lần lượt là \(m_0=\dfrac{1}{12}kg,m_1=200g,m_2=50g\). Bỏ qua lực cản không khí, lực ma sát giữa \(m_1,m_0\) và mặt sàn. Cho hệ số ma sát giữa \(m_1,m_2\) là \(\mu=0,6\). Lấy \(g=10ms^{-2}\). Vật \(m_0\) phải có vận tốc đầu \(v_0\) thỏa mãn điều kiện gì để giữa hai vật \(m_1,m_2\) không xảy ra sự trượt trong quá trình dao động?
cho đoạn thẳng AB2^{100}, cho M_1là trung điểm của AB -M_2là trung điểm của M_1B-M_3là trung điểm của M_2B.........-M_{100}là trung điểm của M_{99}BTính M_1và M_{100}
Đọc tiếp
cho đoạn thẳng AB=\(2^{100}\), cho \(M_1\)là trung điểm của AB
-\(M_2\)là trung điểm của \(M_1\)B
-\(M_3\)là trung điểm của \(M_2\)B.........
-\(M_{100}\)là trung điểm của \(M_{99}\)B
Tính \(M_1\)và \(M_{100}\)
Ba vật có khối lượng , , . Nếu trọng lượng có mối liên hệ là thì khối lượng của chúng có mối liên hệ:
Đọc tiếp
Ba vật có khối lượng ,
,
. Nếu trọng lượng có mối liên hệ là
thì khối lượng của chúng có mối liên hệ:
Đáp án là : m2 = m 2 ( m1 + m3 )
Chúc bạn học tốt ! ![]()
Đúng 0
Bình luận (0)
m1 .10 = P1
m2 . 10 = P2
m3 .10 = P3
= P2 .2 = P1+ P3
= m2 .2.10= A;( P1 + P3 )10=B
=> A = B
=> A : 10 = B : 10=
=====>
Đúng 0
Bình luận (0)
m1 .10 = P1
m2.10 = P2
m3.10 = P3
=> P2.2=P1+P3=m2.2.10=A=(m1+m3)10=B
=> A=B
=> A:10=B:10=
======> 2m2 = m1+ m3
Đúng 0
Bình luận (0)
Xem thêm câu trả lời




















