a) Xét ΔABD vuông tại D và ΔACE vuông tại E có 

AB=AC(ΔABC cân tại A)

\(\widehat{BAD}\) chung

Do đó: ΔABD=ΔACE(cạnh huyền-góc nhọn)

Suy ra: BD=CE(hai cạnh tương ứng)

b) Ta có: ΔABD=ΔACE(cmt)

nên AD=AE(hai cạnh tương ứng)

Xét ΔADE có AD=AE(cmt)

nên ΔADE cân tại A(Định nghĩa tam giác cân)

b) Ta có: ΔABC cân tại A(gt)

nên \(\widehat{ABC}=\dfrac{180^0-\widehat{A}}{2}\)(Số đo của một góc ở đáy trong ΔABC cân tại A)(1)

Ta có: ΔADE cân tại A(cmt)

nên \(\widehat{AED}=\dfrac{180^0-\widehat{A}}{2}\)(Số đo của một góc ở đáy trong ΔADE cân tại A)(2)

Từ (1) và (2) suy ra \(\widehat{AED}=\widehat{ABC}\)

mà \(\widehat{AED}\) và \(\widehat{ABC}\) là hai góc ở vị trí đồng vị

nên DE//BC(Dấu hiệu nhận biết hai đường thẳng song song)

Vì tam giác ABC là tam giác cân nên AM vừa là đường cao vừa là phân giác của góc A

\(\Rightarrow\widehat{MAC}=\frac{70^0}{2}=35^0\)

\(\widehat{ACM}=90^0-35^0=55^0\)

Tam giác ABC cân tại A có AM là đường cao 

suy ra AM là phân giác ABC 

Nên AMB=AMC=70/2=35,5

Xét tam giác AMC có

AMC+ACM+MAC=180

90+ACM+35.5=180

nên ACM=54.5

độ dài các góc không biết nhưng mà biết số đo 

tam giác ABC cân tại A 

=>    góc ACB = (180 - BAC) : 2 => ACB = 55

 AB = AC (đn)

xét tam giác AMC và tam giác AMB có : AM chung

góc AMB = góc AMC = 90 do ...

=> tam giác AMC = tam giác AMB (ch - cgv)

=> CAM = góc BAM (đn)

=> CAM = 35 

...

b2 :

a, xét tam giác ABD và tam giác ACE có: góc A chung

AB = AC do tam giác ABC cân tại A (gt)

góc ADB = góc AEC = 90

=> tam giác ABD = tam giác ACE (ch-cgv)

b, tam giác ABD = tam giác ACE (câu a)

=> góc ABD = góc ACE (đn)

góc ABC = góc ACB do tam giác ABC cân tại A (gt)

góc HBC = góc ABC - góc ABD

góc HCB = góc ACB - góc ACE 

=> góc HBC = góc HCB 

=> tam giác HBC cân tại H (Dh)

còn câu 1

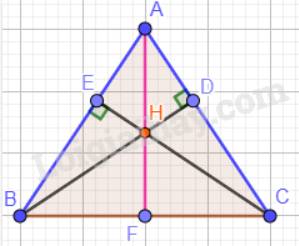
a) Tam giác ABC cân tại A nên: \(\widehat {ABC} = \widehat {ACB} = 70^\circ \).

Tổng ba góc trong một tam giác bằng 180° nên: \(\widehat {BAC} = 180^\circ  - 70^\circ  - 70^\circ  = 40^\circ \).

b) Xét tam giác vuông ADB và tam giác vuông AEC có:

     AB = AC (tam giác ABC cân);

     \(\widehat A\) chung.

Vậy \(\Delta ADB = \Delta AEC\)(cạnh huyền – góc nhọn). Suy ra: BD = CE ( 2 cạnh tương ứng).

c) Trong tam giác ABC có H là giao điểm của hai đường cao BD và CE nên H là trực tâm trong tam giác ABC hay AF vuông góc với BC.

Xét hai tam giác vuông AFB và AFC có:

     AB = AC (tam giác ABC cân);

     AF chung.

Vậy \(\Delta AFB = \Delta AFC\)(cạnh huyền – cạnh góc vuông). Suy ra: \(\widehat {FAB} = \widehat {FAC}\) ( 2 góc tương ứng) hay \(\widehat {BAH} = \widehat {CAH}\).

Vậy tia AH là tia phân giác của góc BAC.

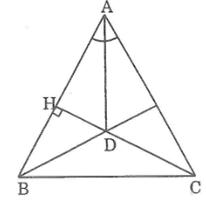
Vì ΔABC cân tại A nên đường phân giác của góc ở đỉnh A cũng là đường cao từ A.

Suy ra: AD ⊥ BC

Ta có: CH ⊥ AB (gt)

Tam giác ABC có hai đường cao AD và CH cắt nhau tại D nên D là trực tâm của ∆ABC

Suy ra BD là đường cao xuất phát từ đỉnh B đến cạnh AC.

Vậy BD ⊥ AC.

a) Xét  và  có

AB=AC;ˆBAH=ˆCAH;AH:chungAB=AC;BAH^=CAH^;AH:chung

  =  (cgc)

b) Có BK = AB  cân tại B

Xét ΔDBC vuông tại D và ΔECB vuông tại E có

BC chung

\(\widehat{DCB}=\widehat{EBC}\)

Do đó: ΔDBC=ΔECB

Suy ra: \(\widehat{IBC}=\widehat{ICB}\)

=>ΔICB cân tại I

=>\(\widehat{DBC}=\dfrac{180^0-110^0}{2}=35^0\)

\(\Leftrightarrow\widehat{ACB}=90^0-35^0=55^0\)

\(\Leftrightarrow\widehat{ABC}=55^0\)

hay \(\widehat{BAC}=70^0\)