cho ham so y=f(x)=(m+1)x
Tìm m để f(2)=4 .Vẽ đồ thị hàm số vs m tìm đc
Những câu hỏi liên quan
cho hàm số y= f(x)=(m+1)x. Tìm m để f(2)=4 . Vẽ đồ thị hàm số với m vừa tìm được
Thay x=2 vào hàm số f(x)=(m+1)x ta được (m+1).2
=> Để f(2)=4 thì m+1 = 4:2 = 2
<=> m = 2-1 = 1
Đúng 0
Bình luận (0)
11 tháng 12 2021 lúc 10:31
Cho hàm số y=f(x)=(m-2)x có đồ thị đi qua điểm A(10;-15)
a) Tìm m
b) Vẽ đồ thị hàm số
c) Tính f(-2); f(-1); f(0); f(1/2)
d) Chứng tỏ rằng: f(-4)-f(-6)=f(2)
a: Thay x=10 và y=-15 vào f(x), ta được:
10m-20=-15
=>10m=5
hay m=1/2
Đúng 1
Bình luận (0)
Cho hàm số y= [ m-1]x+3-2m [ m khác 1] [với m là ham số ]có đồ thị là đường thẳng [d].tìm m ở mỗi trường hợp sau:
A xác định m để đồ thị hàm số song song với đường thẳng y=x-4.vẽ đồ thị hàm số với giá trị vừa tìm được của m
B xác định m để khoảng cách từ gốc tọa độ đến đường thẳng [d] bằng 1
\(a,\Leftrightarrow\left\{{}\begin{matrix}m-1=1\\3-2m\ne-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=2\\m\ne\dfrac{7}{2}\end{matrix}\right.\Leftrightarrow m=2\\ \Leftrightarrow y=x-1\\ b,\text{PT giao Ox và Oy: }y=0\Leftrightarrow x=\dfrac{2m-3}{m-1}\Leftrightarrow OA=\left|\dfrac{2m-3}{m-1}\right|\\ x=0\Leftrightarrow y=3-2m\Leftrightarrow OB=\left|2m-3\right|\\ \text{Gọi H là chân đường cao từ O \rightarrow}\left(d\right)\Leftrightarrow\Leftrightarrow OH=1\\ \text{Áp dụng HTL: }\dfrac{1}{OA^2}+\dfrac{1}{OB^2}=\dfrac{1}{OH^2}=1\\ \Leftrightarrow\dfrac{\left(m-1\right)^2}{\left(2m-3\right)^2}+\dfrac{1}{\left(2m-3\right)^2}=1\\ \Leftrightarrow m^2-2m+2=4m^2-12m+9\\ \Leftrightarrow3m^2-10m+7=0\\ \Leftrightarrow\left[{}\begin{matrix}m=\dfrac{7}{3}\\m=1\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Cho hàm số y = f(x) = (m+1)x – 2 có đồ thị là (d)
a. Tìm m biết rằng đồ thị (d) của hàm số đi qua A(-2:0)
b. Nêu tính chất và vẽ đồ thị hàm số với m tìm được ở câu a .
c. Không tính hãy so sánh f(2√3) và f(3√2)
d. Viết phương trình đường thẳng đi qua B(-1;1)và vuông góc với (d) nói trên
cho hàm số y+ f(x) + (m-1)*x (m khác 1.
a. xét công thức đã cho biết đồ thị hàm số đó đi qua điểm A(1;3)
b. tính f(-1); f(-1/2)
c. tìm x để f(x)=-5; f(x)=-4
d. vẽ đồ thị hàm số đã cho
e. trong các điểm B(-2:4) D(-1;-3); e(1/3;1) điểm nào thuộc đò thị đã cho
a) (1- x2). ( 4x+5/x-1 - 9/x-1)b. x2 + xy - 2x - 2y Câu 5. Cho hàm số: y (2m+1)x - 3 a. Với m3. Tính f (-3); f(0) b. Tìm m để điểm A(2; 3) thuộc đồ thị hàm số. c. Vẽ đồ thị hàm số với m 1 d. Tìm điều kiện để hàm số là hàm bậc nhất. e. Tìm m để hàm số song song với đường thẳng y 5x+1
Đọc tiếp
a) (1- x2). ( 4x+5/x-1 - 9/x-1)
b. x2 + xy - 2x - 2y
Câu 5. Cho hàm số: y = (2m+1)x - 3
a. Với m=3. Tính f (-3); f(0)
b. Tìm m để điểm A(2; 3) thuộc đồ thị hàm số.
c. Vẽ đồ thị hàm số với m= 1
d. Tìm điều kiện để hàm số là hàm bậc nhất.
e. Tìm m để hàm số song song với đường thẳng y= 5x+1
Câu 5:
a: Khi m=3 thì \(f\left(x\right)=\left(2\cdot3+1\right)x-3=7x-3\)
\(f\left(-3\right)=7\cdot\left(-3\right)-3=-21-3=-24\)
\(f\left(0\right)=7\cdot0-3=-3\)
b: Thay x=2 và y=3 vào f(x)=(2m+1)x-3, ta được:
\(2\left(2m+1\right)-3=3\)
=>2(2m+1)=6
=>2m+1=3
=>2m=2
=>m=1
c: Thay m=1 vào hàm số, ta được:
\(y=\left(2\cdot1+1\right)x-3=3x-3\)
*Vẽ đồ thị
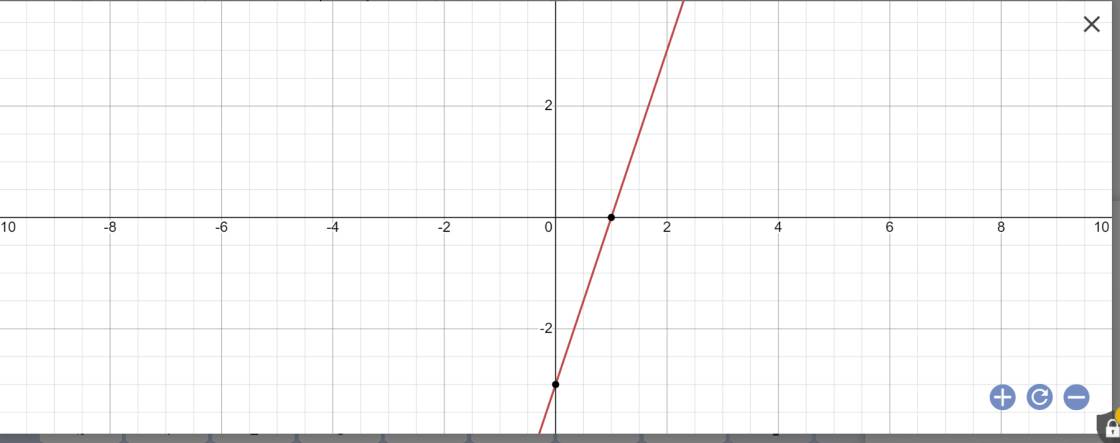
d: Để hàm số y=(2m+1)x-3 là hàm số bậc nhất thì \(2m+1\ne0\)
=>\(2m\ne-1\)
=>\(m\ne-\dfrac{1}{2}\)
e: Để đồ thị hàm số y=(2m+1)x-3 song song với đường thẳng y=5x+1 thì \(\left\{{}\begin{matrix}2m+1=5\\-3\ne1\end{matrix}\right.\)
=>2m+1=5
=>2m=4
=>m=2
Đúng 0
Bình luận (0)
Cho hàm số yf(x). Hàm số yf’(x) có đồ thị như hình vẽ dưới đây.Tìm m để hàm số
y
f
(
x
2
+
m
)
có ba điểm cực trị A. mÎ(3;+∞) B. mÎ[0;3] C. mÎ[0;3) D. mÎ(-∞;0)
Đọc tiếp
Cho hàm số y=f(x). Hàm số y=f’(x) có đồ thị như hình vẽ dưới đây.
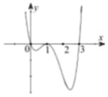
Tìm m để hàm số y = f ( x 2 + m ) có ba điểm cực trị
A. mÎ(3;+∞)
B. mÎ[0;3]
C. mÎ[0;3)
D. mÎ(-∞;0)
cho hàm số y=f(x)=(2m-1)x
a)Tìm m biết f(1)=3
b)Vẽ đồ thị với m vừa tìm đc ở câu a
a)y=f(x)=(2m-1)x\(\Rightarrow y=f\left(3\right)=\left(2m-1\right)3=2m3-3\Rightarrow6m=3\Rightarrow m=6:3=2\)
vậy m=2
b)bn tự vẽ nha
cho hàm số bậc nhất : y = f(x) = (m -1)x +2m +1 (dm).
Khảo sát và vẽ đồ thị hàm số khi m = 2.Tìm m để đồ thị hàm số (dm) đi qua điểm A(4, -1).Tìm m để hàm số nghịch biến trên tập xác định.Tìm điểm cố định của đồ thị hàm số (dm) đi qua.
Khi m = 2 : y = x + 5
TXĐ : D = R.
Tính biến thiên :
a = 1 > 0 hàm số đồng biến trên R.bảng biến thiên :
x | -∞ | +∞ | |
y | -∞ |
| +∞ |
Bảng giá trị :
x | 0 | -5 |
y | 5 | 0 |
Đồ thị hàm số y = x + 5 là đường thẳng đi qua hai điểm A(0, 5) và B(-5; 0).
b/(dm) đi qua điểm A(4, -1) :
4 = (m -1)(-1) +2m +1
<=> m = 2
3. hàm số nghịch biến khi : a = m – 1 < 0 <=> m < 1
4.(dm) đi qua điểm cố định M(x0, y0) :
Ta được : y0 = (m -1)( x0) +2m +1 luôn đúng mọi m.
<=> (x0 + 2) m = y0 – 1 + x0(*)
(*) luôn đúng mọi m khi :
x0 + 2= 0 và y0 – 1 + x0 = 0
<=> x0 =- 2 và y0 = 3
Vậy : điểm cố định M(-2, 3)
Đúng 0
Bình luận (0)