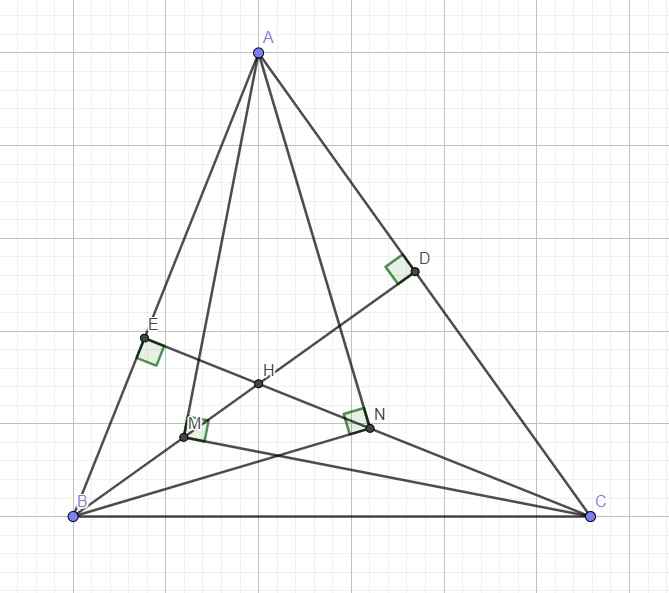
cho tam giác ABC nhọn có 2 đường cao BH và CK cắt nhau tại O.Trên các đoạn OB,OC lần lượt lấy các điểm M,N sao cho AMC=ANB=90 độ.CMR:AM=AN

Những câu hỏi liên quan
Cho tam giác nhọn ABC, 2 đường cao BD và CE cắt nhau tại H. Trên HB và HC lần lượt lấy các điểm M và N sao cho \(\widehat{AMC}\) = \(\widehat{ANB}\) = \(90^o\). Chứng minh rằng: AM = AN
Theo đề có: `ΔAMC` là Δ vuông, đường cao `MD`.
=> `AM^2=AD.AC` (1)
`ΔANB` là Δ vuông, đường cao `NE`:
=> `AN^2=AE.AB` (2)
Lại có: `ΔABD=ΔACE`(g.g)
=> \(\dfrac{AB}{AC}=\dfrac{AD}{AE}\Leftrightarrow AB.AE=AC.AD\left(3\right)\)
Từ (1), (2), (3) suy ra: `AM=AD` (đpcm)
$HaNa$
Đúng 4
Bình luận (1)
cho tam giác nhọn ABC, 2 đường cao BD và CE cắt nhau tại H, trên BH và CH lần lượt lấy điểm M và N sao cho góc AMC=góc ANB=90độ. CMR AM=AN
Xét ΔADB vuông tại D và ΔAEC vuông tại E có
\(\widehat{EAC}\) chung
Do đó: ΔADB\(\sim\)ΔAEC
Suy ra: \(\dfrac{AD}{AE}=\dfrac{AB}{AC}\)
hay \(AD\cdot AC=AB\cdot AE\left(1\right)\)
Xét ΔANB vuông tại N có NE là đường cao ứng với cạnh huyền AB
nên \(AB\cdot AE=AN^2\left(2\right)\)
Xét ΔAMC vuông tại M có MD là đường cao ứng với cạnh huyền AC
nên \(AD\cdot AC=AM^2\left(3\right)\)
Từ (1), (2) và (3) suy ra AM=AN
Đúng 0
Bình luận (0)
cho tam giác ABC có 3 góc nhọn . các đường cao BD ,CE cắt nhau tại H
1/ CMR : tam giác ADB ∞ tam giác AEC
2/ CMR : HB.HD=HC.HE
3/ trên các đoạn thẳng BD và CE lấy lần lượt 2 điểm M , N sao cho ∠AMC =∠ANB = 90o .CMR: AM=AN
1: Xét ΔADB vuông tại D và ΔAEC vuông tại E có
góc DAB chung
=>ΔADB đồng dạng với ΔAEC
2: Xet ΔHEB vuông tại E và ΔHDC vuông tại D có
góc EHB=góc DHC
=>ΔHEB đồng dạng với ΔHDC
=>HE/HD=HB/HC
=>HE*HC=HB*HD
3: ΔAMC vuông tại M có MD vuông góc AC
nên AD*AC=AM^2
ΔANB vuông tại N có NE vuông góc AB
nên AE*AB=AN^2
=>AM=AN
Đúng 1
Bình luận (0)
* Cho tam giác nhọn ABC có hai đường cao BD và CE cắt nhau tại H. Trên HB và HC lần lượt lấy điểm M,N sao cho góc AMC= góc ANB= \(90^0\). Chứng minh:AM=AN
* Cho tam giác ABC vuông tại A, đường cao AH. Biết \(\dfrac{AB}{AC}=\dfrac{20}{21}\)và AH=420. Tính chu vi tam giác ABC
1.
Tam giác AMC vuông tại M với đường cao MD
Áp dụng hệ thức lượng: \(AM^2=AD.AC\) (1)
Tương tự ta có:
\(AN^2=AE.AB\) (2)
Mặt khác xét hai tam giác vuông ABD và ACE có:
\(\widehat{BAC}\) chung
\(\Rightarrow\Delta_VABD\sim\Delta_VACE\) (g.g)
\(\Rightarrow\dfrac{AB}{AC}=\dfrac{AD}{AE}\) \(\Leftrightarrow AB.AE=AC.AD\) (3)
(1);(2);(3) \(\Rightarrow AM^2=AN^2\) \(\Rightarrow AM=AN\)
Bài 2 tham khảo tại đây:
Cho tam giác ABC vuông tại A , đường cao AH . Biết AB/AC = 20/21 , AH = 420 . Tính chu vi tam giác ABC - Hoc24
Đúng 1
Bình luận (0)
Cho tam giác nhọn ABC, hai đường cao BD và CE cắt nhau tại H, Trên HB và HC lần lượt lất các điểm M và N sao cho góc AMC = góc ANB = 90 độ. CMR: AM = AN
Cho tam giác nhọn ABC có hai đường cao BD và Ce cắt nhau tại H . Trên HB và HC lần lượt lấy điểm M và N sao cho góc AMC = góc ANB = 90 độ . Chứng minh AM = AN
Do: Góc ABD = Góc ACE (= 90 - A)
=> Δ ABD ∼ Δ ACE (2 Δ vuông)
=> AD.AC = AE.AB (tỉ lệ đồng dạng)
<=> AM2 = AN2 (Hệ thức lượng trong Δ vuông)
<=> AM = AN
Hay Δ AMN cân tại A.=>....
Đúng 1
Bình luận (5)
cho tam giác nhọn ABC, đường cao BD và CE cắt nhau tại O lấy các điểm M,N thuộc OB,OC sao cho góc AMC và góc CNB =90 độ. AMN là tam giác gì
Xét ΔADB vuông tại D và ΔAEC vuông tại E có
góc DAB chung
=>ΔADB đồng dạng với ΔAEC
=>AD/AE=AB/AC
=>AD*AC=AB*AE
Xet ΔAMC vuông tại M có MD là đường cao
nên AD*AC=AM^2
Xét ΔANB vuông tại N có NE là đường cao
nên AE*AB=AN^2
=>AN=AM
=>ΔAMN cân tại A
Đúng 1
Bình luận (0)
cho tam giác abc có ba goc nhỏ hơn 90 độ. các đường cao bd và ce cắt nhau tại h. a, chứng minh tam giác abc đồng dạng với tam giác ace. b, chứng minh hb.hd=hd.he. c, trên các đoạn thẳng bd và ce lấy lần lượt 2 điểm m và n sao cho góc amc= góc anb=90 độ. chứng minh rằng am=an
a: Xét ΔADB vuông tại D và ΔAEC vuông tại E có
góc A chung
=>ΔABD đồng dạng với ΔACE
b: Xét ΔHEB vuông tại E và ΔHDC vuông tại D có
góc EHB=góc DHC
=>ΔHEB đồng dạng với ΔHDC
=>HE/HD=HB/HC
=>HE*HC=HB*HD
c: Xét ΔAMC vuông tại M có MD vuông góc AC
nên AD*AC=AM^2
ΔANB vuông tại N có NE vuông góc AB
nên AE*AB=AN^2
=>AM=AN
Đúng 0
Bình luận (0)
Cho tam giác nhọn ABC , hai đường cao BD và CE cắt nhau tại H . Trên HB và HC lần lượt lấy M và N sao cho Góc AMC = Góc ANB = 90 độ. C/m : AM = AN
Trong t/g vuông ANB có NE là đường cao: AN^2 = AE.AB
Trong t/g vuông AMC có MD là đường cao: AM^2 = AD.AC
Mà t/g ABD ~ t/g ACE (g.g) nên AB/AC = AD/AE <=> AB.AE = AC.AD
=> AN^2 = AM^2 <=> AN = AM
Đúng 0
Bình luận (0)