x²-2(m-1)x+m²-3m=0

△'=[-(m-1)]²-1(m²-3m)=(m-1)²-(m²-3m)=m²-2m+1-m²+3m= m+1

áp dụng hệ thức Vi-ét ta được 

x1+x2=2(m-1)                                               (1)

x1*x2=m²-3m                                         (2)  

a) để PT có 2 nghiệm phân biệt khi m+1>0 <=> m>-1

b) để PT có duy nhất một nghiệm âm thì x1*x2 <0

e) Áp dụng hệ thức Vi-et, ta được:

\(\left\{{}\begin{matrix}x_1+x_2=2\left(m-1\right)=2m-2\\x_1x_2=m^2-3m\end{matrix}\right.\)

Ta có: \(x_1^2+x_2^2=8\)

\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=8\)

\(\Leftrightarrow\left(2m-2\right)^2-2\cdot\left(m^2-3m\right)-8=0\)

\(\Leftrightarrow4m^2-8m+4-2m^2+6m-8=0\)

\(\Leftrightarrow2m^2-2m-4=0\)(1)

\(\Delta=\left(-2\right)^2-4\cdot2\cdot\left(-4\right)=4+32=36\)

Vì \(\Delta>0\) nên phương trình (1) có hai nghiệm phân biệt là:

\(\left\{{}\begin{matrix}m_1=\dfrac{2-\sqrt{36}}{4}=\dfrac{2-6}{4}=-1\\m_2=\dfrac{2+\sqrt{36}}{4}=\dfrac{2+6}{4}=2\end{matrix}\right.\)

Vậy: Để phương trình có hai nghiệm phân biệt thỏa mãn \(x_1^2+x_2^2=8\) thì \(m\in\left\{-1;2\right\}\)

Ta có : 3x2 – 2(m + 1)x + 3m – 5 = 0 (1)

(1) có hai nghiệm phân biệt khi Δ’ > 0

⇔ (m + 1)2 – 3.(3m – 5) > 0

⇔ m2 + 2m + 1 – 9m + 15 > 0

⇔ m2 – 7m + 16 > 0

⇔ (m – 7/2)2 + 15/4 > 0

Điều này luôn đúng với mọi m ∈ R hay phương trình (1) luôn có hai nghiệm phân biệt., gọi hai nghiệm đó là x1; x2

Khi đó theo định lý Vi–et ta có 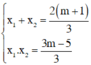 (I)

Phương trình có một nghiệm gấp ba nghiệm kia, giả sử x2 = 3.x1, khi thay vào (I) suy ra :

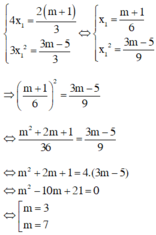
* TH1 : m = 3, pt (1) trở thành 3x2 – 8m + 4 = 0 có hai nghiệm x1 = 2/3 và x2 = 2 thỏa mãn điều kiện.

* TH2 : m = 7, pt (1) trở thành 3x2 – 16m + 16 = 0 có hai nghiệm x1 = 4/3 và x2 = 4 thỏa mãn điều kiện.

Kết luận : m = 3 thì pt có hai nghiệm là 2/3 và 2.

m = 7 thì pt có hai nghiệm 4/3 và 4.

 Với m ≠ -1

    Ta có: Δ   =   ( m   -   3 ) 2   ≥   0 , do đó phương trình luôn luôn có hai nghiệm x 1 ,   x 2

    Lúc đó phương trình đã cho có hai nghiệm x = -1 và x = 4.

a) Xét pt \(x^2-\left(2m-3\right)x+m^2-3m=0\)

Ta có \(\Delta=\left[-\left(2m-3\right)^2\right]-4.1\left(m^2-3m\right)\)\(=4m^2-12m+9-4m^2+12m\)\(=9>0\)

Vậy pt đã cho luôn có 2 nghiệm phân biệt với mọi m.

Câu b mình nhìn không rõ đề, bạn sửa lại nhé.

Xét phương trình x 2 – (2m – 3)x + m 2 – 3m = 0 có a = 1 ≠ 0 và

∆ = ( 2 m – 3 ) 2   –   4 ( m 2 – 3 m ) = 9 > 0    

Phương trình luôn có hai nghiệm phân biệt x 1 ;   x 2

Áp dụng định lý Vi-ét ta có: x 1 + x 2 = 2 m – 3 ; x 1 . x 2 = m 2 – 3 m

Ta có 1 < x 1 < x 2 < 6

⇔ x 1 − 1 x 2 − 1 > 0 x 1 + x 2 > 1 x 1 − 6 x 2 − 6 > 0 x 1 + x 2 < 12 ⇔ x 1 x 2 − x 1 + x 2 + 1 > 0 x 1 + x 2 > 1 x 1 x 2 − 6 x 1 + x 2 + 36 > 0 x 1 + x 2 < 12 ⇔ m 2 − 3 m − 2 m + 3 + 1 > 0 2 m − 3 > 1 m 2 − 3 m − 6 2 m − 3 + 36 > 0 2 m − 3 < 12 ⇔ m 2 − 5 m + 4 > 0 2 m > 4 m 2 − 15 m + 54 > 0 2 m < 15 ⇔ m < 1 m > 4 m > 2 m < 6 m > 9 m < 15 2

⇔ 4 < m < 6

Đáp án: D

Lời giải:

Để pt có 2 nghiệm pb thì:

$\Delta'=(2m-1)^2-4(m^2-3m-4)=8m+17>0\Leftrightarrow m> \frac{-17}{8}$

Áp dụng định lý Viet: 

$x_1+x_2=1-2m$

$x_1x_2=m^2-3m-4$

Khi đó:

$|x_1-x_2|-2=0$

$\Leftrightarrow |x_1-x_2|=2$

$\Leftrightarrow (x_1-x_2)^2=4$

$\Leftrightarrow (x_1+x_2)^2-4x_1x_2=4$
$\Leftrightarrow (1-2m)^2-4(m^2-3m-4)=4$

$\Leftrightarrow 8m+17=4$

$\Leftrightarrow m=\frac{-13}{8}$ (tm)

Lời giải:

Để pt có 2 nghiệm pb thì:

$\Delta'=(2m-1)^2-4(m^2-3m-4)=8m+17>0\Leftrightarrow m> \frac{-17}{8}$

Áp dụng định lý Viet: 

$x_1+x_2=1-2m$

$x_1x_2=m^2-3m-4$

Khi đó:

$|x_1-x_2|-2=0$

$\Leftrightarrow |x_1-x_2|=2$

$\Leftrightarrow (x_1-x_2)^2=4$

$\Leftrightarrow (x_1+x_2)^2-4x_1x_2=4$
$\Leftrightarrow (1-2m)^2-4(m^2-3m-4)=4$

$\Leftrightarrow 8m+17=4$

$\Leftrightarrow m=\frac{-13}{8}$ (tm)

Để pt 1 có 2 nghiệm phân biệt =>\(\Delta\)>0 

<=> (2m-1(² - 4(m²-3m-4( >0

<=> 4m² - 4m + 1 - 4m²+12m+16 > 0

<=>8m +17>0

<=> m>-17/8

=> theo hệ thức Vi ét ta có 

x₁+x₂=-2m+1              *

x₁.x₂=m²-3m-4           *

Theo bài ra  ta có pt

|x1−x2|−2=0

<=> |x1−x2|=2

<=> (x1-x2(²=2²

<=> x_{1^{2 -}} 2x₁.x₂ + x_2²  = 4

<=> (x₁ + x₂ > ²- 4 x₁x₂ = 4  <**>

Thay *,*  vào <**>  ta được :

(-<2m-1>>² - 4<m²-3m-4> = 4 

<=> 4m²-4m+1 - 4m²+12m+16=4

<=> 8m + 17= 4

<=> 8m = 13 

<=> m= 13/8 < t/m >

Vậy m = 13/8 là giá trị cần tìm

Lời giải:

Ta có $x+my=2\Rightarrow x=2-my$. Thay vào PT $(2)$:

$m(2-my)-3my=3m+3$

$\Leftrightarrow -y(m^2+3m)=m+3$

$\Leftrightarrow -ym(m+3)=m+3(*)$

Để hệ PT ban đầu có nghiệm thì $(*)$ có nghiệm $y$

Điều này xảy ra khi $m(m+3)\neq 0\Leftrightarrow m\neq 0;-3$

Khi đó:

$y=\frac{m+3}{-m(m+3)}=-\frac{1}{m}$

$x=2-my=3$

Như vậy:

$y=8x^2$

$\Leftrightarrow \frac{-1}{m}=72\Leftrightarrow m=-72$

Vậy........

\(3x^2-2\left(m+1\right)x+3m-5=0\)

Theo định lý Viet

\(\Rightarrow\left\{{}\begin{matrix}x_1+x_2=\dfrac{-b}{a}\\x_1x_2=\dfrac{c}{a}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_1+x_2=\dfrac{2\left(m+1\right)}{3}\\x_1x_2=\dfrac{3m-5}{3}\end{matrix}\right.\)

Theo yêu cầu đề bài \(x_1=3x_2\)

\(\)\(\Rightarrow\left\{{}\begin{matrix}3x_2+x_2=\dfrac{2\left(m+1\right)}{3}\\3x^2_2=\dfrac{3m-5}{3}\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}4x_2=\dfrac{2\left(m+1\right)}{3}\\3x^2_2=\dfrac{3m-5}{3}\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x_2=\dfrac{m+1}{6}\\3x_2^2=\dfrac{3m-5}{3}\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x_2=\dfrac{m+1}{6}\\3\left(\dfrac{m+1}{6}\right)^2=\dfrac{3m-5}{3}\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x_2=\dfrac{m+1}{6}\\\dfrac{m^2+2m+1}{12}=\dfrac{3m-5}{3}\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x_2=\dfrac{m+1}{6}\\\dfrac{m^2+2m+1}{4}=3m-5\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x_2=\dfrac{m+1}{6}\\m^2+2m+1=12m-20\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_2=\dfrac{m+1}{6}\\m^2-10m+21=0\end{matrix}\right.\)

\(\Leftrightarrow\)\(\left\{{}\begin{matrix}x_2=\dfrac{m+1}{6}\\\left[{}\begin{matrix}m_1=7\\m_2=3\end{matrix}\right.\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}m_1=7\Rightarrow\left\{{}\begin{matrix}x_1=4\\x_2=\dfrac{4}{3}\end{matrix}\right.\\m_2=3\Rightarrow\left\{{}\begin{matrix}x_1=2\\x_2=\dfrac{2}{3}\end{matrix}\right.\end{matrix}\right.\)