Dùng sơ đồ hoocno mà giải đi bạn

(Câu trả lời của alibaba nguyễn đúng mà hài!!!)

Sơ đồ Horner hoạt động như sau:

	1	0	a	b	c
3	1	3	a+9	3a+b+27	9a+3b+c+27
3	1	6	a+27	6a+b+108	27a+6b+c+351
3	...	...	...	...	...

Kẻ bảng, trên dòng đầu tiên ghi các hệ số của đa thức đầu tiên, ở đây là \(1,0,a,b,c\).Theo định lí Bezout thì đa thức sẽ có nghiệm bội 3 là số 3, do đó chừa một cột bên tay trái ghi nghiệm (là số 3).Hạ hệ số (là 1) xuống, thực hiện quy tắc "nhân ngang cộng chéo" (nhân từ nghiệm qua rồi cộng chéo lên).VD: 3 nhân 1 cộng 0 là 3, viết 3. 3 nhân 3 cộng a là a+9, viết a+9. 3 nhân (a+9) cộng b là 3a+b+27, viết 3a+b+27...Để 3 là nghiệm của đa thức thì hệ số cuối cùng là 0, tức là \(9a+3b+c+27=0\).Tự làm tiếp, ra thêm 2 cái phương trình nữa...

Không hiểu gì hết

Cau a va b dat cot tim so du .Vi la phep chia het nen du bang 0.Cau c thi da thuc se chia het cho tich (x+3)(x-3) lam tuong tu hai cau a va b

Chào bạn!

ủng hộ mình lên 360 điểm nha các bạn

bạn có thể động óc suy nghĩ bái toán để được còn hơn là nói như thế

\(f\left(0\right)=c⋮3\) ;

 \(f\left(1\right)=a+b+c⋮3\) mà \(c⋮3\Rightarrow a+b⋮3\)

\(f\left(-1\right)=a-b+c=-2b+\left(a+b+c\right)⋮3\)  mà \(a+b+c⋮3\Rightarrow-2b⋮3\Rightarrow b⋮3\) (do 2 và 3 nguyên tố cùng nhau)

\(\left\{{}\begin{matrix}a+b+c⋮3\\b⋮3\\c⋮3\end{matrix}\right.\) \(\Rightarrow a⋮3\)

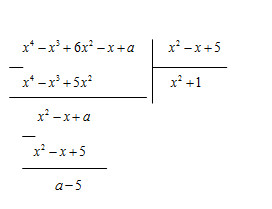
Vậy a = 5 thì đa thức x^4 - x^3 + 6x^2 - x +a chia hết cho đa thức x^2 - x + 5

a) 2x-3=0 <=> x=\(\dfrac{3}{2}\) để \(\left(2x^2-ax+5\right):\left(2x-3\right)\) thì \(2x^2-ax+5=2\)

Thay x= \(\dfrac{3}{2}\) vào \(2x^2-ax+5\), ta được:

\(\dfrac{9}{2}-\dfrac{3}{2}a+5=2\)

<=> \(-\dfrac{3}{2}a=2-5-\dfrac{9}{2}\) <=>a=5

lười quá ~~

bài 1

vì đa thức bị chia bậc 2, đa thức chia bậc nhất

=> đa thức thương sẽ có dạng bx+c

theo đề ta có

\(2x^2-ax+5=\left(bx+c\right)\left(2x-3\right)+2\\ < =>2x^2-ax+5=2bx^2-3bx+2cx-3c+2\\ < =>2x^2-ax+5=2bx^2-x\left(2c-3b\right)-3c+2\\ < =>\left\{{}\begin{matrix}2x^2=2bx^2\\ax=x\left(2c-3b\right)\\5=2-3c\end{matrix}\right.\\ < =>\left\{{}\begin{matrix}b=1\\c=-1\\a=2c-3b\end{matrix}\right.\\ =>a=2\left(-1\right)-3.1\\ =>a=-5\)

vậy a = -5

bài 2 ko hiểu sao mình ko làm được, chắc sai ở đâu đợi mình làm lại nhé