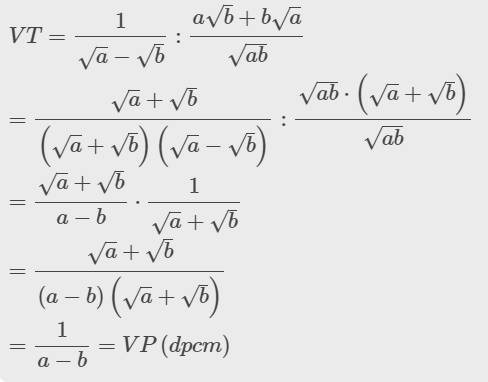\(\dfrac{a\sqrt{b} +a\sqrt{b}}{\sqrt{ab}}\) : \(\dfrac{1}{\sqrt{a}-\sqrt{b}}\) = a-b ( a,b>0; a≠0 )

Những câu hỏi liên quan
rút gọn biểu thức
Adfrac{sqrt{a}-1}{asqrt{a}-a+sqrt{a}}:dfrac{1}{a^2+sqrt{a}} với a 0
Bdfrac{sqrt{a}+sqrt{b}-1}{a+sqrt{ab}}+dfrac{sqrt{a}-sqrt{b}}{2sqrt{ab}}left(dfrac{sqrt{b}}{a-sqrt{ab}}+dfrac{sqrt{b}}{a+sqrt{ab}}right) với a0 b0 và a khác b
Cdfrac{asqrt{b}+b}{a-b}.sqrt{dfrac{ab+b^2-2sqrt{ab^3}}{aleft(a+2sqrt{b}right)+b}}:dfrac{1}{sqrt{a}+sqrt{b}} với ab0
Đọc tiếp
rút gọn biểu thức
A=\(\dfrac{\sqrt{a}-1}{a\sqrt{a}-a+\sqrt{a}}:\dfrac{1}{a^2+\sqrt{a}}\) với a >0
B=\(\dfrac{\sqrt{a}+\sqrt{b}-1}{a+\sqrt{ab}}+\dfrac{\sqrt{a}-\sqrt{b}}{2\sqrt{ab}}\left(\dfrac{\sqrt{b}}{a-\sqrt{ab}}+\dfrac{\sqrt{b}}{a+\sqrt{ab}}\right)\) với a>0 b>0 và a khác b
C=\(\dfrac{a\sqrt{b}+b}{a-b}.\sqrt{\dfrac{ab+b^2-2\sqrt{ab^3}}{a\left(a+2\sqrt{b}\right)+b}}:\dfrac{1}{\sqrt{a}+\sqrt{b}}\) với a>b>0
a: \(=\dfrac{\sqrt{a}-1}{\sqrt{a}\left(a-\sqrt{a}+1\right)}\cdot\dfrac{\sqrt{a}\left(\sqrt{a}+1\right)\left(a-\sqrt{a}+1\right)}{1}\)
\(=a-1\)
b: \(=\dfrac{\sqrt{a}+\sqrt{b}-1}{\sqrt{a}\left(\sqrt{a}+\sqrt{b}\right)}+\dfrac{\sqrt{a}-\sqrt{b}}{2\sqrt{ab}}\cdot\left(\dfrac{\sqrt{b}}{\sqrt{a}\left(\sqrt{a}-\sqrt{b}\right)}+\dfrac{\sqrt{b}}{\sqrt{a}\left(\sqrt{a}+\sqrt{b}\right)}\right)\)
\(=\dfrac{\sqrt{a}+\sqrt{b}-1}{\sqrt{a}\left(\sqrt{a}+\sqrt{b}\right)}+\dfrac{\sqrt{a}-\sqrt{b}}{2\sqrt{ab}}\cdot\dfrac{\sqrt{ab}+b+\sqrt{ab}-b}{\sqrt{a}\left(a-b\right)}\)
\(=\dfrac{\sqrt{a}+\sqrt{b}-1}{\sqrt{a}\left(\sqrt{a}+\sqrt{b}\right)}+\dfrac{1}{\sqrt{a}\left(\sqrt{a}+\sqrt{b}\right)}=\dfrac{1}{\sqrt{a}}\)
c: \(=\dfrac{a\sqrt{b}+b}{a-b}\cdot\sqrt{\dfrac{ab+b^2-2b\sqrt{ab}}{a^2+2a\sqrt{b}+b}}\cdot\left(\sqrt{a}+\sqrt{b}\right)\)
\(=\dfrac{\sqrt{b}\left(a+\sqrt{b}\right)}{\sqrt{a}-\sqrt{b}}\cdot\sqrt{\dfrac{b\left(\sqrt{a}-\sqrt{b}\right)^2}{\left(a+\sqrt{b}\right)^2}}\)
\(=\dfrac{\sqrt{b}\left(a+\sqrt{b}\right)}{\sqrt{a}-\sqrt{b}}\cdot\dfrac{\sqrt{b}\left(\sqrt{a}-\sqrt{b}\right)}{a+\sqrt{b}}=b\)
Đúng 0
Bình luận (0)
Bài: Cho M=\(\dfrac{\sqrt{a}+\sqrt{b}-1}{a+\sqrt{ab}}\) + \(\dfrac{\sqrt{a}-\sqrt{b}}{2\sqrt{ab}}\) . ( \(\dfrac{b}{a-\sqrt{ab}}\) + \(\dfrac{\sqrt{b}}{a+\sqrt{ab}}\) )
a) Tìm đk của a và b để M xác định
b) C/m M > 0
a: ĐKXĐ: \(\left\{{}\begin{matrix}a>0\\b>0\\a< >b\end{matrix}\right.\)
b: \(M=\dfrac{\sqrt{a}+\sqrt{b}-1}{a+\sqrt{ab}}+\dfrac{\sqrt{a}-\sqrt{b}}{2\sqrt{ab}}\cdot\left(\dfrac{b}{a-\sqrt{ab}}+\dfrac{\sqrt{b}}{a+\sqrt{ab}}\right)\)
\(=\dfrac{\sqrt{a}+\sqrt{b}-1}{\sqrt{a}\left(\sqrt{a}+\sqrt{b}\right)}+\dfrac{\sqrt{a}-\sqrt{b}}{2\sqrt{ab}}\cdot\dfrac{b\left(a+\sqrt{ab}\right)+\sqrt{b}\left(a-\sqrt{ab}\right)}{a^2-ab}\)
\(=\dfrac{\sqrt{a}+\sqrt{b}-1}{\sqrt{a}\left(\sqrt{a}+\sqrt{b}\right)}+\dfrac{\sqrt{a}-\sqrt{b}}{a\left(a-b\right)}\cdot\dfrac{ab+b\sqrt{ab}+a\sqrt{b}-b\sqrt{a}}{2\sqrt{ab}}\)
\(=\dfrac{\sqrt{a}+\sqrt{b}-1}{\sqrt{a}\left(\sqrt{a}+\sqrt{b}\right)}+\dfrac{\sqrt{a}-\sqrt{b}}{a\left(\sqrt{a}-\sqrt{b}\right)\cdot\left(\sqrt{a}+\sqrt{b}\right)}\cdot\dfrac{\sqrt{ab}\left(\sqrt{ab}+b+\sqrt{a}-\sqrt{b}\right)}{2\sqrt{ab}}\)
\(=\dfrac{\sqrt{a}+\sqrt{b}-1}{\sqrt{a}\left(\sqrt{a}+\sqrt{b}\right)}+\dfrac{1}{a\left(\sqrt{a}+\sqrt{b}\right)}\cdot\dfrac{\sqrt{ab}+b+\sqrt{a}-\sqrt{b}}{2}\)
\(=\dfrac{2\sqrt{a}\left(\sqrt{a}+\sqrt{b}-1\right)+\sqrt{ab}+b+\sqrt{a}-\sqrt{b}}{2a\left(\sqrt{a}+\sqrt{b}\right)}\)
\(=\dfrac{2a+2\sqrt{ab}-2\sqrt{a}+\sqrt{ab}+b+\sqrt{a}-\sqrt{b}}{2a\left(\sqrt{a}+\sqrt{b}\right)}\)
\(=\dfrac{2a+3\sqrt{ab}-\sqrt{a}+b-\sqrt{b}}{2a\left(\sqrt{a}+\sqrt{b}\right)}\)
\(=\dfrac{2a+3\sqrt{ab}+b-\left(\sqrt{a}+\sqrt{b}\right)}{2a\left(\sqrt{a}+\sqrt{b}\right)}\)
\(=\dfrac{\left(2\sqrt{a}+\sqrt{b}\right)\left(\sqrt{a}+\sqrt{b}\right)-\left(\sqrt{a}+\sqrt{b}\right)}{2a\left(\sqrt{a}+\sqrt{b}\right)}\)
\(=\dfrac{2\sqrt{a}+\sqrt{b}-1}{2a}\)
Giả sử như a=0,1 và b=0,11 thì M<0 nha bạn
=>Đề này sai rồia: ĐKXĐ:
b: \(M=\dfrac{\sqrt{a}+\sqrt{b}-1}{a+\sqrt{ab}}+\dfrac{\sqrt{a}-\sqrt{b}}{2\sqrt{ab}}\cdot\left(\dfrac{b}{a-\sqrt{ab}}+\dfrac{\sqrt{b}}{a+\sqrt{ab}}\right)\)
\(=\dfrac{\sqrt{a}+\sqrt{b}-1}{\sqrt{a}\left(\sqrt{a}+\sqrt{b}\right)}+\dfrac{\sqrt{a}-\sqrt{b}}{2\sqrt{ab}}\cdot\dfrac{b\left(a+\sqrt{ab}\right)+\sqrt{b}\left(a-\sqrt{ab}\right)}{a^2-ab}\)
\(=\dfrac{\sqrt{a}+\sqrt{b}-1}{\sqrt{a}\left(\sqrt{a}+\sqrt{b}\right)}+\dfrac{\sqrt{a}-\sqrt{b}}{a\left(a-b\right)}\cdot\dfrac{ab+b\sqrt{ab}+a\sqrt{b}-b\sqrt{a}}{2\sqrt{ab}}\)
\(=\dfrac{\sqrt{a}+\sqrt{b}-1}{\sqrt{a}\left(\sqrt{a}+\sqrt{b}\right)}+\dfrac{\sqrt{a}-\sqrt{b}}{a\left(\sqrt{a}-\sqrt{b}\right)\cdot\left(\sqrt{a}+\sqrt{b}\right)}\cdot\dfrac{\sqrt{ab}\left(\sqrt{ab}+b+\sqrt{a}-\sqrt{b}\right)}{2\sqrt{ab}}\)
\(=\dfrac{\sqrt{a}+\sqrt{b}-1}{\sqrt{a}\left(\sqrt{a}+\sqrt{b}\right)}+\dfrac{1}{a\left(\sqrt{a}+\sqrt{b}\right)}\cdot\dfrac{\sqrt{ab}+b+\sqrt{a}-\sqrt{b}}{2}\)
\(=\dfrac{2\sqrt{a}\left(\sqrt{a}+\sqrt{b}-1\right)+\sqrt{ab}+b+\sqrt{a}-\sqrt{b}}{2a\left(\sqrt{a}+\sqrt{b}\right)}\)
\(=\dfrac{2a+2\sqrt{ab}-2\sqrt{a}+\sqrt{ab}+b+\sqrt{a}-\sqrt{b}}{2a\left(\sqrt{a}+\sqrt{b}\right)}\)
\(=\dfrac{2a+3\sqrt{ab}-\sqrt{a}+b-\sqrt{b}}{2a\left(\sqrt{a}+\sqrt{b}\right)}\)
\(=\dfrac{2a+3\sqrt{ab}+b-\left(\sqrt{a}+\sqrt{b}\right)}{2a\left(\sqrt{a}+\sqrt{b}\right)}\)
\(=\dfrac{\left(2\sqrt{a}+\sqrt{b}\right)\left(\sqrt{a}+\sqrt{b}\right)-\left(\sqrt{a}+\sqrt{b}\right)}{2a\left(\sqrt{a}+\sqrt{b}\right)}\)
\(=\dfrac{2\sqrt{a}+\sqrt{b}-1}{2a}\)
Giả sử như a=0,1 và b=0,11 thì M<0 nha bạn
=>Đề này sai rồi
Đúng 1
Bình luận (0)
cho M= \(\dfrac{\sqrt{a}+\sqrt{b}-1}{a+a\sqrt{b}}+\dfrac{\sqrt{a}-\sqrt{b}}{2\sqrt{ab}}\left(\dfrac{\sqrt{b}}{a\sqrt{ab}}+\dfrac{\sqrt{b}}{a+\sqrt{ab}}\right)\)
a) tìm điều kiện a và b để M xác định
b) c/m M>0
Chứng minh :
a) dfrac{3x}{2y}+dfrac{3}{2}sqrt{dfrac{3}{5}}-sqrt{dfrac{3}{4}}dfrac{3sqrt{x}}{2}.left(dfrac{sqrt{x}}{y}+sqrt{dfrac{3}{5x}}-sqrt{dfrac{1}{3}}right)
b)ab.sqrt{1+dfrac{1}{a^2b^2}}-sqrt{a^2b^2+1}0 , với a ; b 0
c) left(dfrac{3}{a}sqrt{dfrac{a^3}{b}}-dfrac{1}{2}sqrt{dfrac{4}{ab}}-2sqrt{dfrac{b}{a}}right):sqrt{dfrac{1}{ab}}3a-2b-1 với a, b 0
d)left(sqrt{dfrac{16a}{b}}+3sqrt{4ab}-asqrt{dfrac{36b}{a}}+2sqrt{ab}right):left(sqrt{ab}+dfrac{a}{b}sqrt{dfrac{b}{a}}+sqrt{dfrac{a}{b}}rig...
Đọc tiếp
Chứng minh :
a) \(\dfrac{3x}{2y}+\dfrac{3}{2}\sqrt{\dfrac{3}{5}}-\sqrt{\dfrac{3}{4}}=\dfrac{3\sqrt{x}}{2}.\left(\dfrac{\sqrt{x}}{y}+\sqrt{\dfrac{3}{5x}}-\sqrt{\dfrac{1}{3}}\right)\)
b)\(ab.\sqrt{1+\dfrac{1}{a^2b^2}}-\sqrt{a^2b^2+1}=0\) , với a ; b > 0
c) \(\left(\dfrac{3}{a}\sqrt{\dfrac{a^3}{b}}-\dfrac{1}{2}\sqrt{\dfrac{4}{ab}}-2\sqrt{\dfrac{b}{a}}\right):\sqrt{\dfrac{1}{ab}}=3a-2b-1\) với a, b >0
d)\(\left(\sqrt{\dfrac{16a}{b}}+3\sqrt{4ab}-a\sqrt{\dfrac{36b}{a}}+2\sqrt{ab}\right):\left(\sqrt{ab}+\dfrac{a}{b}\sqrt{\dfrac{b}{a}}+\sqrt{\dfrac{a}{b}}\right)=2\) Với a, b >0
Mọi người giúp tớ với ạ !!!!!! Mình thật sự cần gấp vào ngày mai !!!!
b)CM: \(ab\sqrt{1+\dfrac{1}{a^2b^2}}-\sqrt{a^2b^2+1}=0\)
\(VT=ab\sqrt{\dfrac{a^2b^2+1}{\left(ab\right)^2}}-\sqrt{a^2b^2+1}\)
\(VT=ab\dfrac{\sqrt{a^2b^2+1}}{ab}-\sqrt{a^2b^2+1}\)
\(VT=\sqrt{a^2b^2+1}-\sqrt{a^2b^2+1}\)
\(VT=0=VP\)
Đúng 0
Bình luận (0)
Rút gọn biểu thức :
a) \(\dfrac{a+\sqrt{ab}}{\sqrt{a}+\sqrt{b}}\) ( a > 0 , b > 0 )
b) \(\dfrac{1-8a\sqrt{a}}{1-2\sqrt{a}}\) ( a ≥ 0 , a ≠ \(\dfrac{1}{4}\) )
c) \(\dfrac{1-a}{1+\sqrt{a}}\) ( a ≥ 0 )
d) \(\dfrac{a-3\sqrt{a}}{\sqrt{a}-3}\) ( a ≥ 0 , a ≠ 9 )
a. \(=\dfrac{\sqrt{a}\left(\sqrt{a}+\sqrt{b}\right)}{\sqrt{a}+\sqrt{b}}=\sqrt{a}\)
b. \(=\dfrac{1-\left(2\sqrt{a}\right)^3}{1-2\sqrt{a}}=\dfrac{\left(1-2\sqrt{a}\right)\left(1+2\sqrt{a}+4a\right)}{1-2\sqrt{a}}=1+2\sqrt{a}+4a\)
c. \(=\dfrac{1-\left(\sqrt{a}\right)^2}{1+\sqrt{a}}=\dfrac{\left(1+\sqrt{a}\right)\left(1-\sqrt{a}\right)}{1+\sqrt{a}}=1-\sqrt{a}\)
d. \(=\dfrac{\sqrt{a}\left(\sqrt{a}-3\right)}{\sqrt{a}-3}=\sqrt{a}\)
Đúng 1
Bình luận (0)
Bài: C/m đẳng thức
\(\dfrac{1}{\sqrt{4}-\sqrt{5}}\) : \(\dfrac{a\sqrt{b}+b\sqrt{a}}{\sqrt{ab}}\) = \(\dfrac{1}{a-b}\) với a,b>0 , a,b≠0
CM \(\dfrac{\left(\sqrt{a}-\sqrt{b}\right)^2-4\sqrt{ab}}{\sqrt{a}-\sqrt{b}}.\dfrac{a\sqrt{b}-b\sqrt{a}}{\sqrt{ab}}=a-b\) (a > 0; b > 0)
Chứng minh các đẳng thức sau:
a) \(\left(1+\dfrac{x+\sqrt{x}}{\sqrt{x}+1}\right)\left(1-\dfrac{x-\sqrt{x}}{\sqrt{x}-1}\right)=1-x\)
(Với \(x\ge0;x\ne1\))
b) \(\dfrac{a\sqrt{b}-b\sqrt{a}}{\sqrt{ab}}+\dfrac{a-b}{\sqrt{a}-b}=2\sqrt{a}\)
(Với a>0; b>0; \(a\ne b\))
Câu b bạn sửa lại đề
\(a,VT=\left[1+\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{\sqrt{x}+1}\right]\left[1-\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)}{\sqrt{x}-1}\right]\\ =\left(1+\sqrt{x}\right)\left(1-\sqrt{x}\right)=1-x=VP\\ b,VT=\dfrac{\sqrt{ab}\left(\sqrt{a}-\sqrt{b}\right)}{\sqrt{ab}}+\dfrac{\left(\sqrt{a}-\sqrt{b}\right)\left(\sqrt{a}+\sqrt{b}\right)}{\sqrt{a}-\sqrt{b}}\\ =\sqrt{a}-\sqrt{b}+\sqrt{a}+\sqrt{b}=2\sqrt{a}=VP\)
Đúng 2
Bình luận (1)
a: \(=\left(1+\sqrt{x}\right)\left(1-\sqrt{x}\right)=1-x\)
Đúng 0
Bình luận (0)
Cho a,b,c>0;abc=4
Tính M=\(\sqrt{\dfrac{\sqrt{a}}{\sqrt{ab}+\sqrt{a}+2}}+\sqrt{\dfrac{\sqrt{b}}{\sqrt{bc}+\sqrt{b}+1}}+\sqrt{\dfrac{\sqrt{a}}{\sqrt{ac}+\sqrt{c}+1}}\)
rút gọn : với a,b dương, ab ≠ 0
\(\dfrac{a\sqrt{a}+b\sqrt{b}}{\sqrt{ab}}.\dfrac{1}{\sqrt{a}+\sqrt{b}}\)
\(\dfrac{a\sqrt{a}+b\sqrt{b}}{\sqrt{ab}}.\dfrac{1}{\sqrt{a}+\sqrt{b}}\)
\(=\dfrac{\left(\sqrt{a}+\sqrt{b}\right)\left(a-\sqrt{ab}+b\right)}{\sqrt{ab}}.\dfrac{1}{\sqrt{a}+\sqrt{b}}\)
\(=\dfrac{a-\sqrt{ab}+b}{\sqrt{ab}}\)
Đúng 1
Bình luận (0)