a) Tìm giao điểm A và B của đồ thị (d) hàm số y= x-3 với trục hoành, trục tung
b) Tính diện tích tam giác OAB và góc của đường thẳng (d) với trục Ox
Cho 2 hàm số y = -2x và y = x + 3 a) Tìm tọa độ giao điểm M của 2 đồ thị trên b) Gọi A, B lần lượt là giao điểm của đường thẳng y = x + 3 với trục hoành và trục tung. Tính diện tích của tam giác OAB và tam giác OAM
1/ Vẽ đồ thị hàm số (d): y = -x+1 trên hệ trục toạ độ.
2/ Gọi A, B là giao điểm của đường thẳng (d) với các trục ox, oy. Tính diện tích tam giác OAB.
3/ Viết phương trình đường thẳng (d’) song song với đường thẳng (d) và có tung độ góc là -2.
2: Tọa độ điểm A là:
\(\left\{{}\begin{matrix}y_A=0\\-x_A+1=0\end{matrix}\right.\Leftrightarrow A\left(1;0\right)\)
Tọa độ điểm B là:
\(\left\{{}\begin{matrix}x_B=0\\y_B=-0+1=1\end{matrix}\right.\)
Vậy: B(0;1)
\(S_{OAB}=\dfrac{OA\cdot OB}{2}=\dfrac{1}{2}\)
3: Vì (d')//(d) nên a=-1
Vậy: (d'): y=-x+b
Thay x=0 và y=-2 vào (d'), ta được:
b-0=-2
hay b=-2
Cho hàm số y = 2x và y = -3x + 5
a) Vẽ trên cùng một hệ trục tọa độ, đồ thị hai hàm số trên?
b) Tìm tọa độ giao điểm M của hai đồ thị bằng phương pháp đại số. Gọi A, B lần lượt là giao điểm của đường thẳng y = -3x + 5 với trục hoành và trục tung. Tính diện tích tam giác OAB và diện tích tam giác OMA.
Bải 3: 1/ Vẽ đồ thị hàm số (d): y = -x+1 trên hệ trục toạ độ.
2/ Gọi A, B là giao điểm của đường thẳng (d) với các trục ox, oy. Tính diện tích tam giác OAB.
3/ Viết phương trình đường thẳng (d’) song song với đường thẳng (d) và có tung độ góc là -2.
3: Vì (d')//(d) nên a=-1
Vậy: (d'): y=-x+b
Thay x=0 và y=-2 vào (d'), ta được:
b-0=-2
hay b=-2
Lời giải:
1. Đồ thị $y=-x+1$ có dạng như sau:
2. $A\in Ox$ nên $y_A=0$
Ta có: $y_A=-x_A+1\Leftrightarrow 0=-x_A+1\Leftrightarrow x_A=1$
$B\in Oy$ nên $x_B=0$
Ta có: $y_B=-x_B+1=-0+1=1$
Diện tích tam giác $OAB$:
$S=\frac{1}{2}OA.OB=\frac{1}{2}|x_A|.|y_B|=\frac{1}{2}.1.1=\frac{1}{2}$ (đơn vị diện tích)
3.
Vì $(d')$ song song với $(d)$ nên nó có dạng $y=-x+m$
Tung độ gốc $=-2$ tức là $m=-2$
Vậy $(d'): y=-x-2$
a: Phương trình hoành độ giao điểm là:
2x=-3x+5
=>5x=5
=>x=1
Thay x=1 vào y=2x, ta được:
\(y=2\cdot1=2\)
Vậy: M(1;2)
b: Tọa độ A là:
\(\left\{{}\begin{matrix}y=0\\-3x+5=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=0\\x=\dfrac{5}{3}\end{matrix}\right.\)
Vậy: A(5/3;0)
Tọa độ B là:
\(\left\{{}\begin{matrix}x=0\\y=-3\cdot0+5=5\end{matrix}\right.\)
Vậy: B(0;5)
O(0;0); A(5/3;0); B(0;5)
=>\(OA=\sqrt{\left(\dfrac{5}{3}-0\right)^2+\left(0-0\right)^2}=\dfrac{5}{3}\)
\(OB=\sqrt{\left(0-0\right)^2+\left(5-0\right)^2}=5\)
Vì A,B là giao điểm của (d): y=-3x+5 với trục Ox và trục Oy nên ΔOAB vuông tại O
=>\(S_{AOB}=\dfrac{1}{2}\cdot OA\cdot OB=\dfrac{1}{2}\cdot\dfrac{5}{3}\cdot5=\dfrac{25}{6}\)
M(1;2); O(0;0); A(5/3;0)
\(OA=\sqrt{\left(\dfrac{5}{3}-0\right)^2+\left(0-0\right)^2}=\dfrac{5}{3}\)
\(OM=\sqrt{\left(1-0\right)^2+\left(2-0\right)^2}=\sqrt{5}\)
\(MA=\sqrt{\left(\dfrac{5}{3}-1\right)^2+\left(0-2\right)^2}=\dfrac{2\sqrt{10}}{3}\)
Xét ΔOAM có \(cosAOM=\dfrac{OA^2+OM^2-AM^2}{2\cdot OA\cdot OM}=\dfrac{\sqrt{5}}{5}\)
=>\(sinAOM=\sqrt{1-\left(\dfrac{\sqrt{5}}{5}\right)^2}=\dfrac{2}{\sqrt{5}}\)
\(S_{AOM}=\dfrac{1}{2}\cdot OA\cdot OM\cdot sinAOM\)
\(=\dfrac{1}{2}\cdot\sqrt{5}\cdot\dfrac{5}{3}\cdot\dfrac{2}{\sqrt{5}}=\dfrac{5}{3}\)
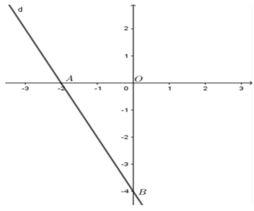
Cho đường thẳng d : y = − 2 x – 4 . Gọi A, B lần lượt là giao điểm của d với trục hoành và trục tung. Tính diện tích tam giác OAB.
A. 2
B. 4
C. 3
D. 8
A (x; 0) là giao điểm của d với trục hoành nên 0 = − 2 x ⇔ x = − 2 ⇒ A ( − 2 ; 0 )
B (0; y) là giao điểm của d với trục tung nên y = − 2 . 0 – 4 ⇔ y = − 4 ⇒ B ( 0 ; − 4 )
Suy ra O A = | − 2 | = 2 ; O B = | − 4 | = 4
Vì tam giác )AB vuông tại O nên S O A B = O A . O B 2 = 2.4 2 = 4 (đvdt)
Đáp án cần chọn là: B
Cho đường thẳng d: y = − 3 x + 2 . Gọi A, B lần lượt là giao điểm của d với trục hoành và trục tung. Tính diện tích tam giác OAB.
A. 4 3
B. − 2 3
C. 3 2
D. 2 3
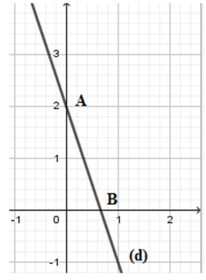
B (x; 0) là giao điểm của d với trục hoành nên 0 = − 3 x + 2 ⇔ x = 2 3 B 2 3 ; 0
A (0; y) là giao điểm của d với trục tung nên y = − 3 . 0 + 2 ⇔ y = 2 ⇒ A ( 0 ; 2 )
Suy ra O A = | 2 | = 2 ; O B = 2 3 = 2 3
Vì tam giác OAB vuông tại O nên SOAB = O A . O B 2 = 2. 2 3 2 = 2 3 (đvdt)
Đáp án cần chọn là: D
tìm giao điểm của đồ thị hàm số y=x-3 với trục tung trục hoành
b,tính góc tạo bởi đường thẳng y=x-3 với trục ox
Cho hàm số y= -2x+3
a) Vẽ đồ thị của hàm số trên
b) Gọi A và B là giao điểm của đồ thị với các trục tọa độ. Tính diện tích tam giác OAB (với O là gốc tọa độ và đơn vị trên các trục tọa độ là centimet)
c) Tính góc tạo bởi đường thẳng y= -2x+3 với trục Ox
cho hai hàm số bậc nhất y=-2x+5(d) và y=0.5x(d') .
a, vẽ đồ thị (d) và(d') của hai hàm số đã cho trên cùng một hệ trục tọa độ xOy
b, tìm tọa độ giao điểm M là giao điểm của hai đô thị vừa vẽ{bằng phép tính}
c, tính góc a tạo bởi đường thẳng (d) với trục hoành Ox
d. gọi giao điểm của (d) với trục Oy là A ,tính chu vi và diện tích tam giác MOA