Chọn A.

Vì 30⁰ và 60⁰  là hai góc phụ nhau nên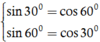 

Suy ra: P = sin30⁰.cos60⁰ + cos30⁰.sin60⁰ = cos60⁰.cos60⁰ + sin60⁰.cos60⁰ = 1.

Chọn D.

Vì 30⁰ và 60⁰  là hai góc phụ nhau nên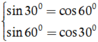 

Do đó: P = cos30⁰.cos60⁰ - sin30⁰.sin60⁰ = cos30⁰.cos60⁰ - cos30⁰.cos60⁰ = 0.

Chọn C.

Dùng bảng giá trị lượng giác các góc đặc biệt ta có

Dung kháng của tụ là \({Z_C} = \dfrac{1}{{\omega C}} = \dfrac{1}{{100\pi .\dfrac{{{{10}^{ - 4}}}}{\pi }}} = 100\Omega \).

Ta có I = 5 A; ${Z_L} = \omega L = 100\pi .0,4 = 40\Omega .$
→ ${U_L} = I{Z_L}$ = 5.40 = 200 V.

a/ Khi vật trượt trên mpn

\(\overrightarrow{F_{ms}}+\overrightarrow{P}+\overrightarrow{N}=m.\overrightarrow{a}\)

\(\Rightarrow\left\{{}\begin{matrix}Ox:P.\sin30^0-F_{ms}=m.a\\P.\cos30=N\end{matrix}\right.\)

\(\Rightarrow\frac{1}{2}mg-\mu mg.\frac{\sqrt{3}}{2}=m.a\)

\(\Rightarrow a\approx3\left(m/s^2\right)\)

\(v^2-v_0^2=2aS\Leftrightarrow v=\sqrt{2.3.165}\approx31,5\left(m/s\right)\)

b/\(v^2-v_0^2=2aS\Leftrightarrow-31,5^2=2.a.121\Leftrightarrow a=-4,1\left(m/s^2\right)\)

\(\overrightarrow{F_{ms}}+\overrightarrow{P}+\overrightarrow{N}=m.\overrightarrow{a}\)

\(\Leftrightarrow m.a=-\mu mg\Leftrightarrow-4,1=-10\mu\Leftrightarrow\mu=0,41\)

Sử dụng đường tròn

Từ thời điểm 0-0.01 s thì góc quay được là \(\varphi = 0.01.\omega = \pi (rad).\)

Thời điểm t =0 ứng với điểm M; thời điểm t = 0.01s ứng với điểm N. Từ M đến N sẽ qua hai điểm P và Q có giá trị (độ lớn) 0.5I₀.

tại P: \(\varphi_1 = t_1 \omega => t_1 = \frac{\pi/3}{100\pi} = \frac{1}{300}s\)

tại Q: \(\varphi_2 = t_2 \omega => t_2 = \frac{\pi/3+\pi/6+\pi/6}{100\pi} = \frac{2}{300}s\)

chọn đáp án. A

A

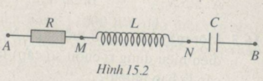
Ta vẽ giản đồ vectơ :  U → = U A M → + U M N → + U N B →

Trong đó  U A M → ↑ ↑ I → ;   U N B → ⊥ I →

Hai tam giác ABM và NBM bằng nhau (có các cạnh lần lượt bằng nhau) dẫn tới kết quả hai tam giác vuông HAB và HNM đồng dạng, suy ra

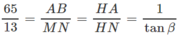
⇒ tan β = 16/65 = 1/5

Trên Hình 15.1.G

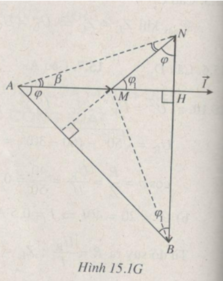
2 β  = φ 1

⇒ sin φ 1  = sin2 β

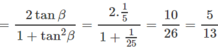
Mặt khác theo Hình 15.1G, ta có :

φ + φ1 = π/2 ⇒ cosφ = sinφ1 = 5/13

\(\Delta\varphi=\omega\frac{x_2-x_1}{v}=5\pi\)

hai giao động ngược pha