Với mọi a;b dương ta có:

\(a^4+b^4\ge\dfrac{1}{2}\left(a^2+b^2\right)^2=\dfrac{1}{2}\left(a^2+b^2\right).\left(a^2+b^2\right)\ge\dfrac{1}{2}.2ab.\left(a^2+b^2\right)=ab\left(a^2+b^2\right)\)

Và: \(a^3+b^3=\left(a+b\right)\left(a^2+b^2-ab\right)\ge\left(a+b\right)\left(2ab-ab\right)=ab\left(a+b\right)\)

Do đó:

\(A\le\sum\dfrac{ab}{ab\left(a^2+b^2\right)+ab}+2020=\sum\dfrac{1}{a^2+b^2+1}+2020\)

Đặt \(\left(a^2;b^2;c^2\right)=\left(x^3;y^3;z^3\right)\Rightarrow xyz=1\)

\(\Rightarrow A\le\sum\dfrac{1}{x^3+y^3+1}+2020\le\sum\dfrac{1}{xy\left(x+y\right)+1}+2020\)

\(A\le\sum\dfrac{xyz}{xy\left(x+y\right)+xyz}+2020=\sum\dfrac{z}{x+y+z}+2020=1+2020=2021\)

Dấu "=" xảy ra khi \(a=b=c=1\)

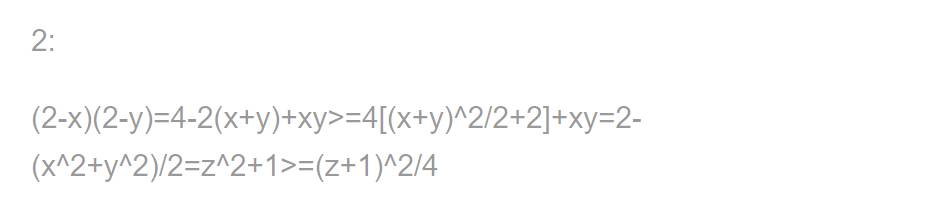
Tương tự, ta được:

\(\left(2-y\right)\left(2-z\right)>=\dfrac{\left(x+1\right)^2}{4}\)

và \(\left(2-z\right)\left(2-x\right)>=\left(\dfrac{y+1}{2}\right)^2\)

=>8(2-x)(2-y)(2-z)>=(x+1)(y+1)(z+1)

(x+yz)(y+zx)<=(x+y+yz+xz)^2/4=(x+y)^2*(z+1)^2/4<=(x^2+y^2)(z+1)^2/4

Tương tự, ta cũng co:

\(\left(y+xz\right)\left(z+y\right)< =\dfrac{\left(y^2+z^2\right)\left(x+1\right)^2}{2}\)

và \(\left(z+xy\right)\left(x+yz\right)< =\dfrac{\left(z^2+x^2\right)\left(y+1\right)^2}{2}\)

Do đó, ta được:

\(\left(x+yz\right)\left(y+zx\right)\left(z+xy\right)< =\left(x+1\right)\left(y+1\right)\left(z+1\right)\)

=>ĐPCM

Lời giải:

Áp dụng BĐT Cauchy-Schwarz:

\(\sum \frac{c^{2013}}{a+b-c}=\sum \frac{c^{4024}}{ac^{2011}+bc^{2011}-c^{2012}}\geq \frac{(\sum a^{2012})^2}{a^{2011}(b+c)+b^{2011}(c+a)+c^{2011}(b+a)-\sum a^{2012}}\)

Ta sẽ CM:

\(a^{2011}(b+c)+b^{2011}(c+a)+c^{2011}(b+a)-\sum a^{2012}\leq \sum a^{2012}\)

\(\Leftrightarrow a^{2011}(a-b)+a^{2011}(a-c)+b^{2011}(b-a)+b^{2011}(b-c)+c^{2011}(c-a)+c^{2011}(c-b)\geq 0\)

\(\Leftrightarrow \sum (a-b)(a^{2011}-b^{2011})\geq 0\Leftrightarrow \sum (a-b)^2(a^{2010}+...+b^{2010})\geq 0\) (luôn đúng)

Do đó: \(\sum \frac{c^{2013}}{a+b-c}\geq \frac{(\sum a^{2012})^2}{\sum a^{2012}}=\sum a^{2012}\)

Dấu "=" xảy ra khi $a=b=c$. Tức là $ABC$ là tam giác đều.

\(A=\dfrac{a^3}{b+c+d}+\dfrac{b^3}{a+c+d}+\dfrac{c^3}{a+b+d}+\dfrac{d^3}{a+b+c}\)

\(=\dfrac{a^4}{ab+ac+ad}+\dfrac{b^4}{ab+bc+bd}+\dfrac{c^4}{ac+bc+cd}+\dfrac{d^4}{ad+bd+cd}\)

\(\ge\dfrac{\left(a^2+b^2+c^2+d^2\right)^2}{2\left(ab+ac+ad+bc+bd+cd\right)}\) (bđt Cauchy Shwarz dạng Engel)

Cần chứng minh \(\dfrac{a^2+b^2+c^2+d^2}{2\left(ab+ac+ad+bc+bd+cd\right)}\ge\dfrac{1}{3}\)

\(\Leftrightarrow3a^2+3b^2+3c^2+3d^2\ge2\left(ab+ac+ad+bc+bd+cd\right)\)

\(\Leftrightarrow\left(a-b\right)^2+\left(a-c\right)^2+\left(a-d\right)^2+\left(b-d\right)^2+\left(b-c\right)^2+\left(c-d\right)^2\ge0\) *đúng*

Vậy ta có đpcm.

Dấu "=" xảy ra khi a = b = c = d

Lời giải:
\((a+b+c)(\frac{1}{a+b}+\frac{1}{b+c}+\frac{1}{a+c})=\frac{a}{a+b}+\frac{a}{b+c}+\frac{a}{a+c}+\frac{b}{a+b}+\frac{b}{b+c}+\frac{b}{a+c}+\frac{c}{a+b}+\frac{c}{b+c}+\frac{c}{a+c}\)

$\Leftrightarrow 2018.\frac{1}{2018}=\frac{a+b}{a+b}+\frac{b+c}{b+c}+\frac{c+a}{c+a}+\frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b}$

$\Leftrightarrow 1=1+1+1+S$

$S=1-1-1-1=-2$