Tìm các số nguyên dương m,n thỏa mãn:2m-3n=7

Những câu hỏi liên quan
Cho m và n là các số nguyên dương thỏa mãn (m,n)=1. Tìm ước chung lớn nhất của 4m+3n và 5m+2n
Trong một số trường hợp, có thể sử dụng mối quan hệ đặc biệt giữa ƯCLN, BCNN và tích của hai số nguyên dương a, b, đó là : ab = (a, b).[a, b], trong đó (a, b) là ƯCLN và [a, b] là BCNN của a và b. Việc chứng minh hệ thức này khụng khú :
Theo định nghĩa ƯCLN, gọi d = (a, b) => a = md ; b = nd với m, n thuộc Z+ ; (m, n) = 1 (*)
Từ (*) => ab = mnd2 ; [a, b] = mnd
=> (a, b).[a, b] = d.(mnd) = mnd2 = ab
=> ab = (a, b).[a, b] . (**)
Đúng 0
Bình luận (0)
Tìm tất cả các số nguyên dương n thỏa mãn n+1 và 3n+6 là các số lập phương,đồng thời 2n+5 là số nguyên tố.
Đặt \(3n+6=x^3,n+1=y^3\)vì \(n\inℕ^∗\)nên \(x>1,y>3\)và x,y nguyên dương
\(\left(3n+6\right)-\left(n+1\right)=x^3-y^3\)
\(\Leftrightarrow2n+5=\left(x-y\right)\left(x^2+xy+y^2\right)\)(1)
Vì 2n+5 là số nguyên tố nên chỉ có 2 ước là 1 và 2n+5 mà (x-y) và (x2+xy+y2) cũng là 2 ước của 2n-5 nên:
\(\orbr{\begin{cases}x-y=1,x^2+xy+y^2=2n+5\\x^2+xy+y^2=1,x-y=2n+5\end{cases}}\)mà \(x>1,y>3\)nên vế dưới không thể xảy ra.
Vậy \(\hept{\begin{cases}x=y+1\\x^2+xy+y^2=2n+5\end{cases}}\)thay vế trên vào vế dưới\(\Rightarrow\left(y+1\right)^2+y\left(y+1\right)+y^2=2n+5\)
\(\Rightarrow3y^2+3y+1=2n+5\)
Vậy ta xét \(\hept{\begin{cases}3y^2+3y+1=2n+5\\y^3=n+1\Rightarrow2y^3=2n+2\end{cases}}\)trừ 2 biểu thức vế theo vế:
\(\Rightarrow-2y^3+3y^2+3y+1=3\Leftrightarrow\left(y+1\right)\left(y-2\right)\left(1-2y\right)=0\)
Vì nguyên dương nên nhận y=2--->n=7
cho m&n là 2 số nguyên dương thỏa mãn(m&n)=1.tìm ƯCLN của 4m+3n&5m+2n
1. Chứng minh rằng nếu các số nguyên dương x, y thỏa mãn điều kiện x2 + y2 + 2x(y+1) − 2y là số chính phương thì x y.2. Tìm các số nguyên dương n để n4 + 2n3 + 3n3 + 3n + 7 là số chính phương.3. Tìm các số tự nhiên m,n thỏa mãn 2m + 3 n2.4. Tìm các số tự nhiên n để n2 + n + 2 là tích của k số nguyên dương liên tiếp với k ≥ 2.5. Tìm các số tự nhiên n để 36n − 6 là tích của k số nguyên dương liên tiếp với k ≥ 2.6. Tìm số tự nhiên n lớn nhất để 427 +4500 +4n là số chính phương.7. Tìm các số...
Đọc tiếp
1. Chứng minh rằng nếu các số nguyên dương x, y thỏa mãn điều kiện x2 + y2 + 2x(y+1) − 2y là số chính phương thì x = y.
2. Tìm các số nguyên dương n để n4 + 2n3 + 3n3 + 3n + 7 là số chính phương.
3. Tìm các số tự nhiên m,n thỏa mãn 2m + 3 = n2.
4. Tìm các số tự nhiên n để n2 + n + 2 là tích của k số nguyên dương liên tiếp với k ≥ 2.
5. Tìm các số tự nhiên n để 36n − 6 là tích của k số nguyên dương liên tiếp với k ≥ 2.
6. Tìm số tự nhiên n lớn nhất để 427 +4500 +4n là số chính phương.
7. Tìm các số nguyên tố p để 2p - 1 - 1 / p là số chính phương
Tìm tất cả các số nguyên dương thỏa mãn 2n2+3n+1 là số chính phương và n+5 là số nguyên tố
Tìm số nguyên dương n thỏa mãn
2
C
n
0
+
5
C
n
1
+
8
C
n
2
+
.
.
.
+
3
n
+
2
C
n
n
A. n 5 B. n 7 C. n 8 D. n 10
Đọc tiếp
Tìm số nguyên dương n thỏa mãn 2 C n 0 + 5 C n 1 + 8 C n 2 + . . . + 3 n + 2 C n n
A. n = 5
B. n = 7
C. n = 8
D. n = 10
![]()
Viết ngược lại biểu thức của S, ta được
![]()
Cộng (1) và (2) vế theo vế và kết hợp với công thức ![]() ta có
ta có
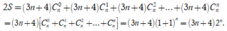
Theo giả thiết: ![]()
Chọn B.
Đúng 0
Bình luận (0)
Tìm số nguyên dương n thỏa mãn
2
C
n
0
+
5
C
n
1
+
8
C
n
2
+
...
+
3
n
+
2
C
n
n
1600.
A. 5 B. 7 C.10 D. 8
Đọc tiếp
Tìm số nguyên dương n thỏa mãn 2 C n 0 + 5 C n 1 + 8 C n 2 + ... + 3 n + 2 C n n = 1600.
A. 5
B. 7
C.10
D. 8
Đáp án B
Ta có: S = 2 C n 0 + ... + C n n + 3 C n 1 + 2 C n 2 + 3 C n 3 + ... + n C n n
Xét khai triển 1 + x n = C n 0 + C n 1 x + ... + C n n x n
Đạo hàm 2 vế ta có: n 1 + x n − 1 = C n 1 + 2 C n 2 x + 3 C n 3 x 2 + ... + n C n n x n − 1
Cho x = 1 ta có: 2 n = C n 0 + C n 1 + ... + C n n ; n .2 n − 1 = C n 1 + 2 C n 2 + 3 C n 3 + ... + n C n n
Do đó S = 2.2 n + 3. n 2 n − 1 = 1600 → S H I F T − C A L C n = 7.
Đúng 0
Bình luận (0)
Tìm số nguyên dương n thỏa mãn
2
C
n
0
+
5
C
n
1
+
8
C
n
2
+
..
+
3
n
+
2
C
n
n
1600
A. 5 B. 7 C. 10 D. 8
Đọc tiếp
Tìm số nguyên dương n thỏa mãn 2 C n 0 + 5 C n 1 + 8 C n 2 + .. + 3 n + 2 C n n = 1600
A. 5
B. 7
C. 10
D. 8
Đáp án B
Ta có S = 2 C n 0 + ... + C n n + 3 C n 1 + 2 C n 2 + 3 C n 3 + .. + n C n n
Xét khai triển 1 + x n = C n 0 + C n 1 x + ... + C n n x n
Đạo hàm 2 vế ta có n 1 + x n − 1 = C n 1 + 2 C n 2 x + ... + n C n n x n − 1
Cho x = 1 ta có 2 n = C n 1 + 2 C n 2 + ... + C n n ; n 2 n − 1 = C n 1 + 2 C n 2 + 3 C n 3 + ... + n C n n
Do đó S = 2.2 n + 3. n .2 n − 1 = 1600 → S H I F T − C A L C n = 7
Đúng 0
Bình luận (0)
1, Tìm các số tự nhiên x,y sao cho: p^x y^4 + 4 biết p là số nguyên tố2, Tìm tất cả số tự nhiên n thỏa mãn 2n + 1, 3n + 1 là các số cp, 2n + 9 là các số ngtố3, Tồn tại hay không số nguyên dương n để n^5 – n + 2 là số chính phương4, Tìm bộ số nguyên dương ( m,n ) sao cho p m^2 + n^2 là số ngtố và m^3 + n^3 – 4 chia hết cho p5, Cho 3 số tự nhiên a,b,c thỏa mãn điều kiện: a – b là số ngtố và 3c^2 ab +c ( a + b )Chứng minh: 8c + 1 là số cp6, Cho các số nguyên dương phân biệt x,y sao cho ( x – y...
Đọc tiếp
1, Tìm các số tự nhiên x,y sao cho: p^x = y^4 + 4 biết p là số nguyên tố
2, Tìm tất cả số tự nhiên n thỏa mãn 2n + 1, 3n + 1 là các số cp, 2n + 9 là các số ngtố
3, Tồn tại hay không số nguyên dương n để n^5 – n + 2 là số chính phương
4, Tìm bộ số nguyên dương ( m,n ) sao cho p = m^2 + n^2 là số ngtố và m^3 + n^3 – 4 chia hết cho p
5, Cho 3 số tự nhiên a,b,c thỏa mãn điều kiện: a – b là số ngtố và 3c^2 = ab +c ( a + b )
Chứng minh: 8c + 1 là số cp
6, Cho các số nguyên dương phân biệt x,y sao cho ( x – y )^4 = x^3 – y^3
Chứng minh: 9x – 1 là lập phương đúng
7, Tìm các số nguyên tố a,b,c sao cho a^2 + 5ab + b^2 = 7^c
8, Cho các số nguyên dương x,y thỏa mãn x > y và ( x – y, xy + 1 ) = ( x + y, xy – 1 ) = 1
Chứng minh: ( x + y )^2 + ( xy – 1 )^2 không phải là số cp
9, Tìm các số nguyên dương x,y và số ngtố p để x^3 + y^3 = p^2
10, Tìm tất cả các số nguyên dương n để 49n^2 – 35n – 6 là lập phương 1 số nguyên dương
11, Cho các số nguyên n thuộc Z, CM:
A = n^5 - 5n^3 + 4n \(⋮\)30
B = n^3 - 3n^2 - n + 3 \(⋮\)48 vs n lẻ
C = n^5 - n \(⋮\)30
D = n^7 - n \(⋮\)42











