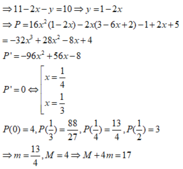Thao m =3 và HPT ta có: 

\(\left\{{}\begin{matrix}\left(3-1\right)x+y=3\\x+\left(3-1\right)y=2\end{matrix}\right.\)

⇔\(\left\{{}\begin{matrix}2x+y=3\\x+2y=2\end{matrix}\right.\)

⇔\(\left\{{}\begin{matrix}4x+2y=6\\x+2y=2\end{matrix}\right.\)

⇔\(\left\{{}\begin{matrix}4x+2y=6\\3x=4\end{matrix}\right.\)

⇔\(\left\{{}\begin{matrix}x=\dfrac{4}{3}\\y=\dfrac{1}{3}\end{matrix}\right.\)

Vậy với m=3 thì HPT có nghiệm (x;y) = (\(\dfrac{4}{3};\dfrac{1}{3}\))

a) Thay m=3 vào hệ phương trình, ta được:

\(\left\{{}\begin{matrix}2x+y=3\\x+2y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x+y=3\\2x+4y=4\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}-3y=-1\\2x+y=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{1}{3}\\2x=3-y=3-\dfrac{1}{3}=\dfrac{8}{3}\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{4}{3}\\y=\dfrac{1}{3}\end{matrix}\right.\)

Vậy: Khi m=3 thì hệ phương trình có nghiệm duy nhất là \(\left\{{}\begin{matrix}x=\dfrac{4}{3}\\y=\dfrac{1}{3}\end{matrix}\right.\)

b) \(\left\{{}\begin{matrix}\left(m-1\right)x+y=m\\x+\left(m-1\right)y=2\end{matrix}\right.\)

⇔\(\left\{{}\begin{matrix}x=2-\left(m-1\right)y\\\left(m-1\right)\left(2-\left(m-1\right)y\right)+y=m\end{matrix}\right.\)

⇔\(\left\{{}\begin{matrix}x=2-my+y\\\left(m-1\right)\left(2-my+y\right)+y=m\left(1\right)\end{matrix}\right.\)

Từ (1) ta có: 

\(\left(m-1\right)\left(2-my+y\right)=y=m\)

⇔\(2m-m^2y+my-2+my-y+y=m\)

⇔\(-m^2y+2my=-2m+2+m\)

⇔\(my\left(-m+2\right)=-2m+2+m\) (2)

Trường hợp 1: 

\(-m+2=0\)

⇔m= \(\mp\)2

*Thay m=2 vào (2) ta có: 0y=0 ⇒m=2 (chọn)

*Thay m=-2 và (2) ta có: 0y= -4 ⇒m= -2 (loại)

Trường hợp 2:

-m+2 \(\ne0\)

⇔m\(\ne\) 2

⇒HPT có nghiệm duy nhất: 

\(my=\dfrac{-2m+2+m}{-m+2}\)

⇒\(y=\dfrac{-2m+2+m}{-m+2}.\dfrac{1}{m}\)

⇒\(y=\dfrac{-2m+2+m}{-m^2+2m}\)

⇒\(x=2-m.\dfrac{-2m+2+m}{-m^2+2m}+\dfrac{-2m+2+m}{-m^2+2m}\)

Theo bài ra ta có: 

\(2x^2-7y=1\)

⇔\(2.\left(2-m.\dfrac{-2m+2+m}{-m^2+2m}+\dfrac{-2m+2+m}{-m^2+2m}\right)^2-7\left(\dfrac{-2m+2+m}{-m^2+2m}\right)=1\)

\(2.\left(2-\dfrac{2m^2-2m-m^2}{-m^2+2m}+\dfrac{-2m+2+m}{-m^2+2m}\right)^2-\dfrac{14m-14-7m}{-m^2+2m}=1\)

Có gì bạn giải nốt nha, phương trình cũng "đơn giản" rồi 

Mình bấm máy tính Casio nó ra kết quả m=1 

nên với m =1 thì Thỏa mãn yêu cầu đề bài

:))))))))))

a: Ta có: \(x^2=3-2\sqrt{2}\)

nên \(x=\sqrt{2}-1\)

Thay \(x=\sqrt{2}-1\) vào A, ta được:

\(A=\dfrac{\left(\sqrt{2}+1\right)^2}{\sqrt{2}-1}=\dfrac{3+2\sqrt{2}}{\sqrt{2}-1}=7+5\sqrt{2}\)

[2x-2=0=>x=1

x-1=0=>x=1

x+1=0=>x=-1

5=0=>x=5

\(x+y\le xy\Rightarrow\dfrac{1}{x}+\dfrac{1}{y}\le1\)

\(M=\dfrac{1}{2\left(x^2+y^2\right)+y^2}+\dfrac{1}{2\left(x^2+y^2\right)+x^2}\le\dfrac{1}{4xy+y^2}+\dfrac{1}{4xy+x^2}\)

\(B\le\dfrac{1}{25}\left(\dfrac{4}{xy}+\dfrac{1}{y^2}\right)+\dfrac{1}{25}\left(\dfrac{4}{xy}+\dfrac{1}{x^2}\right)=\dfrac{1}{25}\left(\dfrac{1}{x^2}+\dfrac{1}{y^2}+\dfrac{2}{xy}+\dfrac{6}{xy}\right)\)

\(M\le\dfrac{1}{25}\left[\left(\dfrac{1}{x}+\dfrac{1}{y}\right)^2+\dfrac{3}{2}\left(\dfrac{1}{x}+\dfrac{1}{y}\right)^2\right]=\dfrac{1}{10}\left(\dfrac{1}{x}+\dfrac{1}{y}\right)^2\le\dfrac{1}{10}\)

\(M_{max}=\dfrac{1}{10}\) khi \(x=y=2\)

a: \(M=\dfrac{x^2-3x+2x^2+6x-3x^2-9}{\left(x-3\right)\left(x+3\right)}=\dfrac{3}{x+3}\)

a: |2x-3|=1

=>2x-3=1 hoặc 2x-3=-1

=>x=1(nhận) hoặc x=2(loại)

KHi x=1 thì \(A=\dfrac{1+1^2}{2-1}=2\)

b: ĐKXĐ: x<>-1; x<>2

\(B=\dfrac{2x^2-4x+3x+3-2x^2-1}{\left(x-2\right)\left(x+1\right)}=\dfrac{-x+2}{\left(x-2\right)\left(x+1\right)}=\dfrac{-1}{x+1}\)