cho 9 chấm tròn (như hình vẽ):
hãy nối các điểm lại với nhau sao cho tạo thành 4 đoạn thẳng và các đoạn thẳng đều đi qua tất cả các điểm
Năm hình tròn tạo thành 9 miền như hình vẽ. Hai trong số các miền đó được gắn mác 12 và 15. Hãy sử dụng các số 3,4,5,6,7,8,9 và 11 để bán cho các miền còn lại (mỗi số gán cho một miền duy nhất) sao cho tổng các số trong mỗi hình tròn là 20.
Cho \(\widehat {xOy}\). Vẽ cung tròn tâm O, cung này cắt Ox, Oy theo thứ tự tại M, N. Vẽ hai cung tròn tâm M và tâm N có cùng bán kính sao cho chúng cắt nhau tại điểm P nằm trong \(\widehat {xOy}\). Nối O với P (Hình 16). Hãy chứng minh rằng , từ đó suy ra OP là tia phân giác của \(\widehat {xOy}\).
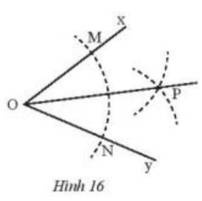
Vì M, N thuộc đường tròn tâm O có cùng bán kính nên OM = ON = bán kính cung tròn tâm O
Từ M, N vẽ 2 cung tròn có cùng bán kính và 2 đường tròn cắt nhau tại P
Suy ra P thuộc cả 2 cung tròn tâm M, N có cùng bán kính nên MP = NP
Xét tam giác OMP và tam giác ONP ta có :
OM = ON
OP cạnh chung
MP = NP
\(\Rightarrow \Delta{OMP}=\Delta{ONP}\) ( c-c-c )
\( \Rightarrow \widehat {MOP} = \widehat {PON}\) (2 góc tương ứng)
Do đó, OP là phân giác \(\widehat {xOy}\)
hãy vẽ 9 chấm tròn trên 2 đoạn thẳng cắt nhau ,sao cho mỗi đoạn thẳng đều có 5 chấm tròn
TOÁN LỚP 2 NHA TRANG 58 BÀI 4 ĐÓ MÌNH KO VẼ HÌNH ĐƯỢC
Người ta nối các điểm giữa của hình vuông lại với nhau để được hình vuông mới như hình vẽ .Biết diện tích hình vuông bé nhất bằng 50 cm2
Người ta nối các điểm giữa của hình vuông lại với nhau để được hình vuông mới như hình vẽ .Biết diện tích hình vuông bé nhất bằng 50 cm2
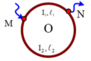
Nối hai điểm M và N của vòng tròn dây dẫn như hình vẽ với hai cực một nguồn điện. Tính cảm ứng từ tại tâm O của vòng tròn, coi cảm ứng từ trong các dây nối với vòng tròn không đáng kể
A. B = I 2 I 2 .10 − 7 R 2
B. B = I 1 I 2 + I 2 I 2 .10 − 7 R 2
C. B = I 1 I 1 .10 − 7 R 2
D. B = 0
Cho nửa đường tròn tâm I đường kính AB. Lấy điểm C thuộc nửa đường tròn và H là hình chiếu của C trên AB. Vẽ đường tròn (C;CH). Vẽ các tiếp tuyến AE và BF với đường tròn (C;CH) sao cho các tiếp điểm E, F không trùng với H.
CMR: a, AE//BF
b, EA . BF = CH2
c, EF là tiếp tuyến của đường tròn (I)
Hình tự vẽ
a) BF ; AE tiếp tuyến
=> \(\widehat{BFE}=\widehat{EFB}=90^{\text{o}}\)
Ta có \(\widehat{BFE}+\widehat{EFB}=180^{\text{o}}\)
=> FB//AE
b) Xét tam giác vuông ACE ; ACH
AC2 = AE2 + CE2 = AH2 + HC2
=> AE = AH (CE = HC)
Tương tự ta có FB = HB
lại có \(\widehat{ACB}=90^{\text{o}}\left(\text{thuộc (I) ; đường kính AB}\right)\)
Xét tam giác vuông ABC vuông tại C ; đường cao AH có
AH.AB = CH2 = AE.FB
c) Ta có \(\widehat{ECF}=\widehat{ECA}+\widehat{ACB}+\widehat{FCB}=2\widehat{ACB}=180^o\)
(Vì \(\widehat{ECA}=\widehat{ACH};\widehat{HCB}=\widehat{FCB}\))
=> E;C;F thẳng hàng
mà EC = CF
=> C trung điểm EF
mà I trung điểm AB
=> CI đường trung bình hình thang EABF
=> EA//CI//FB
=> \(\widehat{ECI}=90^{\text{o}}\)
=> EF tiếp tuyến (I)
cho các số 1,2,3,4,5,6.hãy xếp nó thành các chấm tròn sao cho các số trên một đường thẳng cộng lại đều bằng 9.
Cho một hình vuông. Nối trung điểm hai cạnh liên tiếp của hình vuông đó với nhau ta được hình vuông thứ hai. Nối trung điểm hai cạnh liên tiếp của hình vuông thứ hai với nhau ta được hình vuông thứ ba. Nối hai đường chéo của hình vuông đã cho ta được hình như hình vẽ sau:
Tính tổng diện tích tất cả các tam giác có trong hình vẽ. Biết diện tích hình vuông đã cho là 156,25.
cho một hình vuông. nối trung điểm 2 cạnh liên tiếp của hình vuông đó với nhau ta được hình vuông thứ 2. nối trung điểm 2 cạnh liên tiếp của hình vuông thứ 2 với nhau ta được hình vuông thứ 3. nối 2 đường chéo của hình vuông đã cho ta được hình như hình vẽ sau:
tính tổng diện tích tất cả các tam giác có trong hình vẽ. biết diện tích hình vuông đã cho là 156,25cm2
diện tích tất cả tam giác gấp 5 lần diện tích hình vuông.
Ta có : 156,25 x 5 = 781,25 (cm2)