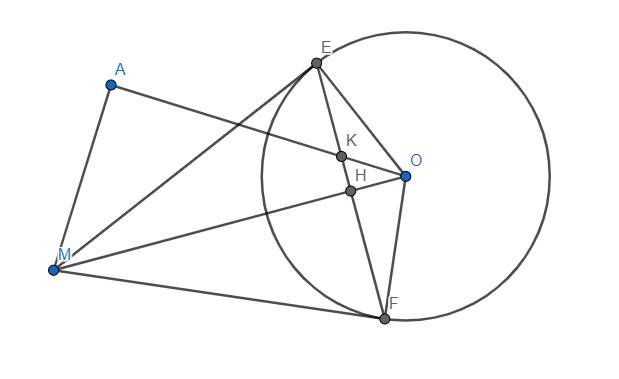
a) Cho đường tròn (O) và điểm A nằm trên đường tròn . Từ A vẽ đường thẳng d vuông góc OA tại A. Chứng tỏ đường thẳng d là tiếp tuyến của đường tròn (O)
b) cho đường tròn (O) và điểm A nằm bên ngòai đường tròn. Vẽ đường tròn tâm I đường kính AO, đường tròn (I) cắt đường tròn (O) tại B và C. Chứng tỏ rằng AB và AC là tiếp tuyến của đường tròn (O)