Mỗi xe đi 100km thì chi phí là:

1 200 000x(100:50)=2 400 000(đồng)

Đội đó có 10 xe thì chi phí là:

2 400 000x10=24 000 000(đồng)

Đáp số:24 000 000 đồng

6 chiếc xe đi được:50x6=300(km)

10 chiếc xe đi được:100x10=1000(km)

10 chiếc xe mỗi chiếc đi 100 km thì chi phí là:1000x1 200 000:300=4 000 000(đồng)

Đ/s:4 000 000 đồng

Ta có : một xe/1km=1200000/50=2400(đồng)

=>Đoàn xe có 10 xe tiêu hết số tiền là :2400*100*10=24000000(đồng)

4000000 đồng nha

Nhớ k cho mk nha

Câu 1 : 

Nửa chu vi miếng đất hình chữ nhật là: 100:2=50(m)

Gọi chiều dài miếng đất là: x(m)

      chiều rộng miếng đất là: y(m)

                (y<x<50)

Miếng đất hình chữ nhật có nửa chu vi là 50m . 

=> Phương trình: x+y=50 (1)

5 lần chiều rộng hơn 2 lần chiều dài 40m.

\(\Rightarrow\) Phương trình : \(-2x+5y=40\left(2\right)\)

Từ (1) và (2) ta có hệ phương trình:

\(\hept{\begin{cases}x+y=50\\-2x+5y=40\end{cases}}\)

\(\hept{\begin{cases}y=50-x\\-2x+5\left(50-x\right)=40\end{cases}}\)

\(\Leftrightarrow\hept{\begin{cases}y=50-x\\-2x+250-5x=40\end{cases}}\)

\(\Leftrightarrow\hept{\begin{cases}y=50-x\\-2x-5x=40-250\end{cases}}\)

\(\Leftrightarrow\hept{\begin{cases}y=50-x\\-7x=-210\end{cases}}\)

\(\Leftrightarrow\hept{\begin{cases}y=50-30\\x=30\end{cases}}\)

\(\Leftrightarrow\hept{\begin{cases}y=20\left(nhận\right)\\x=30\left(nhận\right)\end{cases}}\)

Vậy miếng đất hình chữ nhật có chiều dài là 30m và chiều rộng 20m

Câu 2 : 

a) Gọi số người lớn trong gia đình bác Tú là: x(người)

          Số trẻ em trong gia đình bác Tú là: y(người) 

\(\left(y< x< 12\right)\left(x,y\inℕ^∗\right)\)

Gia đình bác Tú có 12 người. 

=> Phương trình: x+y=12x (1)

Năm nay, gia đình bác dự định đi du lịch trong hè với tổng số tiền là 30 triệu đồng. Trong đó, mỗi người lớn chi phí cho chuyến đi hết 3 triệu, mỗi trẻ em chi phí hết 1,5 triệu.

=> Phương trình \(3x+1,5y=30\left(2\right)\)

Từ (1) và (2) ta có hệ phương trình:

\(\hept{\begin{cases}x+y=12\\3x+1,5y=30\end{cases}}\)

\(\Leftrightarrow\hept{\begin{cases}x=8\left(nhận\right)\\y=4\left(nhận\right)\end{cases}}\)

Vậy gia đình bác Tú có 88 người lớn và 44 trẻ em.

b) Gọi số tiền mà mỗi người lớn phải trả trong chuyến du lịch đó hết x(triệu)

          số tiền mà mỗi trẻ em phải trả trong chuyến du lịch đó hết y(triệu)

(y<x<43,6) 

Năm ngoái, gia đình bác cũng với số người đó nhưng tiêu tốn chi phí cho cả chuyến du lịch của gia đình hết 43,6 triệu.

\(\Rightarrow\)Phương trình : \(x+y=43,6\left(1\right)\)

Mỗi người lớn chi phí nhiều hơn một trẻ em là 1,7 triệu.

\(\Rightarrow\) Phương trình : \(x-y=1,7\left(2\right)\)

Từ (1) và (2) ta có hệ phương trình:

\(\hept{\begin{cases}x+y=43,6\\x-y=1,7\end{cases}}\)

\(\Leftrightarrow\hept{\begin{cases}x=22,65\left(nhận\right)\\y=20,95\left(nhận\right)\end{cases}}\)

Vậy trong chuyến du lịch đó chi phí cho mỗi người lớn là 22,65 triệu, trẻ em là 20,95 triệu. 

Đáp án C

Giả sử có n máy thì chi phí cố định là

50 n   n = 1 ; 2 ; 3...8

Để in 50000 tờ cần 5000 3600. n = 125 9 n (giờ in).

Chi phí cho n máy chạy trong một giờ là 10 6 n + 10  nghìn đồng.

Khi đó, tổng chi phí để in 50000 tờ quảng cáo là:

f n = 50 n + 10 6 n + 10 .125 9 n = 450 n 2 + 7500 n + 1250 9 n

( Đến đây các em có thể thay 4 giá trị xem giá trị nào cho kết quả nhỏ nhất).

Ta có: f ' n = 0 ⇔ n = 5 3 10 ≈ 5 , 27

Lại có: f 5 < f 6  nên ta cần sử dụng 5 máy để chi phí nhỏ nhất.

Đáp án C

Giả sử có n máy thì chi phí cố định là 50n ( n   =   1 ;   2 ;   3 ; . . . . ; 8 )

Để tin 50000 tờ cần 5000 3600 n   =   125 9 n  (giờ in)

Chi phí cho n máy chạy trong một giờ là: 10(6n + 10) nghìn đồng

Khi đó, tổng chi phí để in 50000 tờ quảng cáo là :

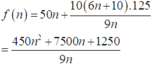
(thay 4 giá trị xem giá trị nào cho kết quả nhỏ nhất)

Lại có f(5) < f(6) nên ta sử dụng 5 máy để chi phí nhỏ nhất

Chọn C.

Gọi x 0 ≤ x ≤ 8 ; x ∈ Z  là số máy in sử dụng trong một giờ để được lãi nhiều nhất. Khi đó chi phí dành cho x máy in trong một giờ là 10(6x+10)=60x+100 nghìn đồng.

Chi phí vận hành 50x nghìn đồng.

Số bản in trong một giờ là 3600x suy ra thời gian để in xong 50000 tờ quảng cáo là 50000 3600 x = 125 9 x  giờ

Vậy tổng chi phí là f x = 60 x + 100 25 9 x + 50 x  nghìn đồng

Để lãi là nhiều nhất thì tổng chi phí là thấp nhất, vậy ta tìm giá trị nhỏ nhất của tổng chi phí.

Thay các giá trị x = 1 ; 2 ; 3 ; 4 ; 5 ; 6 ; 7 ; 8  ta thấy giá trị nhỏ nhất là  f 5 = 12250 9 .

Đáp án C

Gọi f n  là hàm chi phí in 50000 tờ quảng cáo 0 < n ≤ 8 ; n ∈ ℕ . Ta cần tìm n để f(n) có giá trị thấp nhất. Theo giả thiết f(n) bao gồm chi phí vận hành cho n máy là 50n nghìn  đồng. Và chi phí chạy máy sản xuất 50000 tờ quảng cáo là: 50000 3600 n 10 6 n + 10 = 2500 9 n 3 n + 5  

Vậy  f ( n ) = 50 n + 2500 9 n 3 n + 5 = 50 n + 250 9 n + 2500 3

Đến đây ta có thể khảo sát hàm f(n) với nnguyên để tìm chi phí thấp nhất hoặc kiểm tra trực tiếp bốn đáp án và được kết quả thấp nhất với n=5.