Cho đường tròn đường kính AB, lấy điểm C bất kì thuộc đường tròn ( C # A , C # B ). Chứng minh rằng : tam giác ABC vuông

Những câu hỏi liên quan
Cho đường tròn (O), AB là một đường kính bất kì và C là một điểm thuộc đường tròn. Vẽ C’ đối xứng với điểm C qua AB (h.57). Chứng minh rằng điểm C’ cũng thuộc đường tròn (O).
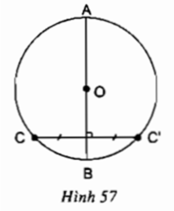
Do C và C' đối xứng nhau qua AB nên AB là đường trung trực của CC'
⇒ O nằm trên đường trung trực của CC'
⇒ OC = OC' = R
⇒ C' cũng thuộc đường tròn (O)
Đúng 0
Bình luận (0)
Cho đường tròn (O), AB là một đường kính bất kì và C là một điểm thuộc đường tròn. Vẽ C’ đối xứng với điểm C qua AB (h.57). Chứng minh rằng điểm C’ cũng thuộc đường tròn (O).
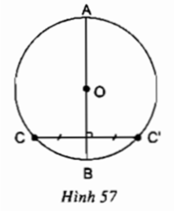
Do C và C' đối xứng nhau qua AB nên AB là đường trung trực của CC'
⇒ O nằm trên đường trung trực của CC'
⇒ OC = OC' = R
⇒ C' cũng thuộc đường tròn (O)
Đúng 0
Bình luận (0)
Cho nửa đường tròn tâm O, đường kính AB. Kẻ tia Ax vuông góc với AB ( tia Ax và nửa đường tròn thuộc cùng một nửa mặt phẳng bờ AB. Lấy một điểm C bất kì thuộc nửa đường tròn ( C khác A và B). Qua O kẻ một đường thẳng song song với BC cắt tia Ax tại M và cắt AC tại F. a, Tính MB biết BC = 5 , AC = 8 b, D là giao MB và (O) cmr ∆MFD ~ ∆MBO
Cho đường tròn (O) có AB là đường kính. Trên tia đối của tia AB lấy điểm C nằm ngoài đường tròn. Lấy điểm M bất kì nằm trên đường tròn (O). Gọi P là giao điểm của MB và đường vuông góc với AB tại C. Chọn khẳng định đúng. A. Tứ giác PMAC là tứ giác nội tiếp B. Tam giác BCM vuông C. Tam giác BCP có CM là đường trung tuyến. D. Tất cả sai
Đọc tiếp
Cho đường tròn (O) có AB là đường kính. Trên tia đối của tia AB lấy điểm C nằm ngoài đường tròn. Lấy điểm M bất kì nằm trên đường tròn (O). Gọi P là giao điểm của MB và đường vuông góc với AB tại C. Chọn khẳng định đúng.
A. Tứ giác PMAC là tứ giác nội tiếp
B. Tam giác BCM vuông
C. Tam giác BCP có CM là đường trung tuyến.
D. Tất cả sai
Chọn đáp án A.
Ta có:
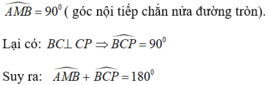
Do đó, tứ giác PMAC là tứ giác nội tiếp
Đúng 0
Bình luận (0)
cho nửa đường tròn tâm o đường kính ab trên nửa đường tròn lấy điểm c sao cho ca <cb,vẽ ch vuông góc với ab (h thuộc ab).trên cung bc lấy điểm d bất kì (d khác b và c),gọi e là giao diểm của ch và ad.
a)chứng minh tứ giác bdhe nội tiếp đường tròn
b)chứng minh ac bình phương = ae.ad
a: góc EHB+góc EDB=180 độ
=>BDHE nội tiếp
b: Xét ΔACE và ΔADC có
góc ACE=góc ADC
góc CAE chung
=>ΔACE đồng dạng với ΔADC
=>AC^2=AE*AD
Đúng 0
Bình luận (0)
Cho nửa đường tròn tâm O, đường kính AB = 2R. Trên nửa đường tròn lấy điểm C bất kì (C khác A và B). Tiếp tuyến tại C và tiếp tuyến tại A cắt nhau tại M. a) Chứng minh bốn điểm, O, A, M, C cùng thuộc một đường tròn. b) AC cắt OM tại H, chứng minh AC vuông góc với OM và 2.OH OM =R mũ 2.
a: Xét tứ giác OAMC có
\(\widehat{OAM}+\widehat{OCM}=180^0\)
Do đó: OAMC là tứ giác nội tiếp
Đúng 0
Bình luận (0)
1. Cho nửa đường tròn tâm O đường kính AB. Vẽ các tiếp tuyến Ax, By ( Ax, By cùng thuộc nửa mặt phẳng chứa nửa đường tròn bờ AB). Gọi M là điểm bất kì thuộc nửa đường tròn. Tiếp tuyến tại M cắt Ax, By tại C và D.a) Chứng minh đường tròn đường kính CD tiếp xúc với AB.b) Tìm vị trí của điểm M để hình thang ABDC có chu vi nhỏ nhất.c) Kẻ MH⊥AB tại H. Chứng minh rằng BC đi qua trung điểm I của MH.(Chỉ cần làm câu c thôi mấy câu để có số liệu thôi)
Đọc tiếp
1. Cho nửa đường tròn tâm O đường kính AB. Vẽ các tiếp tuyến Ax, By ( Ax, By cùng thuộc nửa mặt phẳng chứa nửa đường tròn bờ AB). Gọi M là điểm bất kì thuộc nửa đường tròn. Tiếp tuyến tại M cắt Ax, By tại C và D.
a) Chứng minh đường tròn đường kính CD tiếp xúc với AB.
b) Tìm vị trí của điểm M để hình thang ABDC có chu vi nhỏ nhất.
c) Kẻ MH⊥AB tại H. Chứng minh rằng BC đi qua trung điểm I của MH.
(Chỉ cần làm câu c thôi mấy câu để có số liệu thôi)
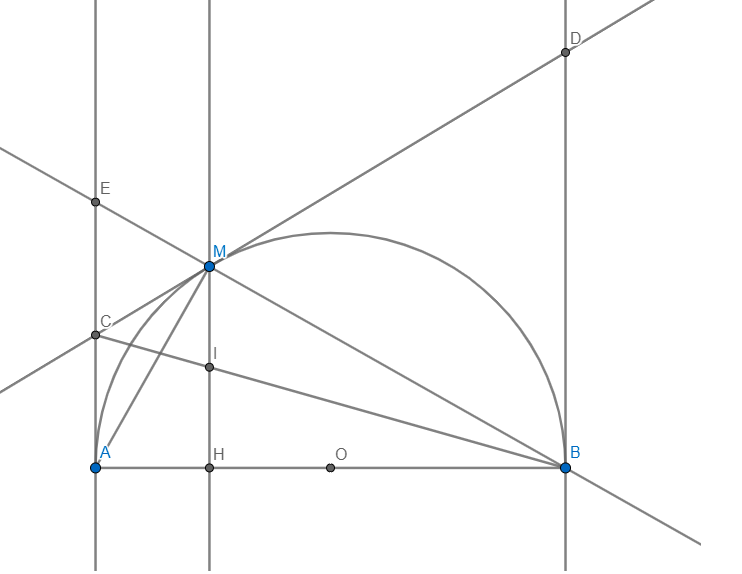
c) BM cắt Ax tại E.BC cắt MH tại I
Vì AB là đường kính nên \(\angle AMB=90\)
Vì CM,CA là tiếp tuyến nên \(CM=CA\)
Ta có tam giác AME vuông tại M có \(CM=CA\Rightarrow C\) là trung điểm AE
Vì \(MH\parallel AE(\bot AB)\) \(\Rightarrow\left\{{}\begin{matrix}\dfrac{IH}{AC}=\dfrac{BI}{BC}\\\dfrac{IM}{CE}=\dfrac{BI}{BC}\end{matrix}\right.\Rightarrow\dfrac{IH}{AC}=\dfrac{IM}{CE}\)
mà \(AC=CE\Rightarrow IH=IM\) nên ta có đpcm
Đúng 2
Bình luận (0)
cho đường tròn tâm O đường kính AB. Lấy I là điểm bất kì trên AB(I khác O). Kẻ PQ vuông góc với AB tại I cắt đường tròn tại P,Q. Lấy M thuộc PQ( M khác I). AM, BM cắt đường tròn ở C,D. DC cắt AB tại K. chứng minh rằng KP,KQ là tiếp tuyến của đường tròn tâm O
Cho nửa đường tròn tâm O đường kính AB. Vẽ các tiếp tuyến Ax, By ( Ax và By và nửa đường tròn cùng thuộc về 1 nửa mặt phẳng bờ là AB ). Gọi M là 1 điểm bất kì thuộc nửa đường tròn. Tiếp tuyến tại M cắt Ax, By theo thứ tự tại C và D. Lấy I là trung điểm của CD. Chọn câu sai : A. Đường tròn có đường kính CD và tiếp xúc với ABB. Đường tròn có đường kính CD cắt AB C. IO ⊥ ABD. IO D C /2
Đọc tiếp
Cho nửa đường tròn tâm O đường kính AB. Vẽ các tiếp tuyến Ax, By ( Ax và By và nửa đường tròn cùng thuộc về 1 nửa mặt phẳng bờ là AB ). Gọi M là 1 điểm bất kì thuộc nửa đường tròn. Tiếp tuyến tại M cắt Ax, By theo thứ tự tại C và D. Lấy I là trung điểm của CD. Chọn câu sai :
A. Đường tròn có đường kính CD và tiếp xúc với AB
B. Đường tròn có đường kính CD cắt AB
C. IO ⊥ AB
D. IO = D C /2
Trên nửa đường tròn tâm O đường kính AB 2R, lấy điểm C (C khác A, B), từ C kẻ CH vuông góc AB (H thuộc AB). Gọi D là điểm bất kì trên đoạn CH (D khác C và H), đường thẳng AD cắt nửa đường tròn tại điểm thứ hai là E.a. CM tứ giác BHDE nội tiếp.b. CM AD.EC CD.ACc. Khi điểm C di động trên nửa đường tròn (C khác A, B và điểm chính giữa cung AB), xác định vị trí của điểm C sao cho chu vi tam giác COH đạt GTLN.Dạ bày em câu (c) với ạ, giải chi tiết giúp em:)
Đọc tiếp
Trên nửa đường tròn tâm O đường kính AB = 2R, lấy điểm C (C khác A, B), từ C kẻ CH vuông góc AB (H thuộc AB). Gọi D là điểm bất kì trên đoạn CH (D khác C và H), đường thẳng AD cắt nửa đường tròn tại điểm thứ hai là E.
a. CM tứ giác BHDE nội tiếp.
b. CM AD.EC = CD.AC
c. Khi điểm C di động trên nửa đường tròn (C khác A, B và điểm chính giữa cung AB), xác định vị trí của điểm C sao cho chu vi tam giác COH đạt GTLN.
Dạ bày em câu (c) với ạ, giải chi tiết giúp em:")
Đặt chu vi COH là \(P=OC+OH+CH\)
Ta có:
\(P=OC+OH+CH\le OC+\sqrt{2\left(OH^2+CH^2\right)}=OC+\sqrt{2OC^2}=OC\left(1+\sqrt{2}\right)=R\left(1+\sqrt{2}\right)\)
Dấu "=" xảy ra khi \(OH=CH\Rightarrow\Delta OCH\) vuông cân tại H
\(\Rightarrow\widehat{COH}=45^0\) hay C là điểm nằm trên cung AB sao cho OC hợp với AB 1 góc 45 độ
//Phía trên sử dụng BĐT \(a+b\le\sqrt{2\left(a^2+b^2\right)}\) để đánh giá
Đúng 5
Bình luận (0)

















