A x B 1 2 C y Tìm mối liên hệ giữa widehat{xAB} ; widehat{ABC} ; widehat{BCy} để Ax // Cy
Đọc tiếp
Tìm mối liên hệ giữa \(\widehat{xAB}\) ; \(\widehat{ABC}\) ; \(\widehat{BCy}\) để Ax \(\)// Cy
Những câu hỏi liên quan
Tìm mối liên hệ giữa a và b để
\(lim\dfrac{\sqrt{x^2-3x}+ax}{bx-1}\)=3
Giới hạn này x tiến tới đâu nhỉ?
Đúng 0
Bình luận (0)
a) Cho tam giác ABC không phải là tam giác vuông có BC a,AC b,AB c và R là bán kính của đường trong ngoại tiếp tam giác đó. Vẽ đường kính BD.i) Tính sin widehat {BDC} theo a và R.ii) Tìm mối liên hệ giữa hai góc widehat {BAC} và widehat {BDC}. Từ đó chứng minh rằng 2R frac{a}{{sin A}}.b) Cho tam giác ABC với góc A vuông. Tính sinA và so sánh a với 2R để chứng tỏ ta vẫn có công thức 2R frac{a}{{sin A}}.
Đọc tiếp
a) Cho tam giác ABC không phải là tam giác vuông có \(BC = a,AC = b,AB = c\) và R là bán kính của đường trong ngoại tiếp tam giác đó. Vẽ đường kính BD.
i) Tính \(\sin \widehat {BDC}\) theo a và R.
ii) Tìm mối liên hệ giữa hai góc \(\widehat {BAC}\) và \(\widehat {BDC}\). Từ đó chứng minh rằng \(2R = \frac{a}{{\sin A}}.\)
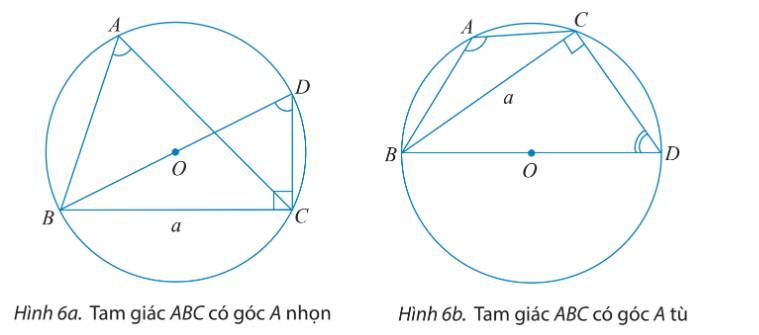
b) Cho tam giác ABC với góc A vuông. Tính sinA và so sánh a với 2R để chứng tỏ ta vẫn có công thức \(2R = \frac{a}{{\sin A}}.\)
a) Tam giác BDC vuông tại C nên \(\sin \widehat {BDC} = \frac{{BC}}{{BD}} = \frac{a}{{2R}}.\)
b)
TH1: Tam giác ABC có góc A nhọn
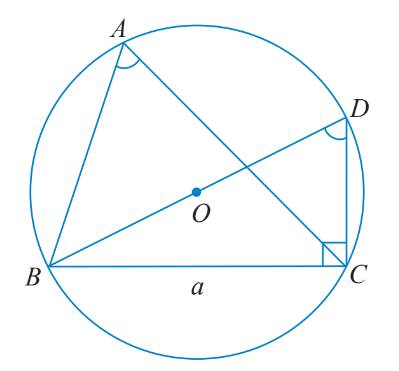
\(\widehat {BAC} = \widehat {BDC}\) do cùng chắn cung nhỏ BC.
\( \Rightarrow \sin \widehat {BAC} = \sin \widehat {BDC} = \frac{a}{{2R}}.\)
TH2: Tam giác ABC có góc A tù
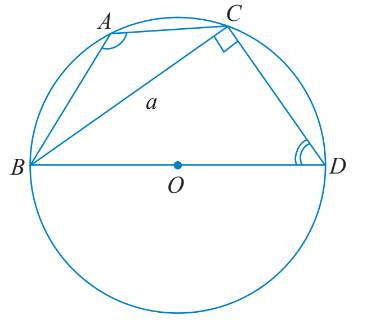
\(\widehat {BAC} + \widehat {BDC} = {180^o}\) do ABDC là tứ giác nội tiếp (O).
\( \Rightarrow \sin \widehat {BAC} = \sin ({180^o} - \widehat {BAC}) = \sin \widehat {BDC} = \frac{a}{{2R}}.\)
Vậy với góc A nhọn hay tù ta đều có \(2R = \frac{a}{{\sin A}}.\)
b) Nếu tam giác ABC vuông tại A thì BC là đường kính của (O).
Khi đó ta có: \(\sin A = \sin {90^o} = 1\) và \(a = BC = 2R\)
Do đó ta vẫn có công thức: \(2R = \frac{a}{{\sin A}}.\)
Đúng 0
Bình luận (0)
Tìm mối liên hệ giữa a, b, c, để phương trình \(\left(b^2+c^2\right)x^2-2acx+a^2-b^2=0\) có nghiệm ?
Phương trình (b2+c2)x2−2acx+a2−b2=0(b2+c2)x2−2acx+a2−b2=0 có nghiệm khi và chỉ khi b2+c2≠0b2+c2≠0 và Δ′≥0Δ′≥0
b2+c2≠0b2+c2≠0 suy ra b và c không đồng thời bằng 0.
Δ′=(−ac)2−(b2+c2)(a2−b2)=a2c2−a2b2+b4−a2c2+b2c2=−a2b2+b4+c2b2=b2(−a2+b2+c2)Δ′≥0⇒b2(−a2+b2+c2)≥0Δ′=(−ac)2−(b2+c2)(a2−b2)=a2c2−a2b2+b4−a2c2+b2c2=−a2b2+b4+c2b2=b2(−a2+b2+c2)Δ′≥0⇒b2(−a2+b2+c2)≥0)
Vì b2≥0⇒−a2+b2+c2≥0⇔b2+c2≥a2b2≥0⇒−a2+b2+c2≥0⇔b2+c2≥a2
Vậy với a2≤b2+c2a2≤b2+c2 thì phương trình đã cho có nghiệm.
Đúng 0
Bình luận (0)
Tìm các mối liên hệ giữa các tham số a và b sao cho hàm số
y
f
x
2
x
+
a
sin
x
+
b
cos
x
luôn tăng trên R? A.
1
a
+
1
b
1
B.
a
+
2
b
≥
1...
Đọc tiếp
Tìm các mối liên hệ giữa các tham số a và b sao cho hàm số y = f x = 2 x + a sin x + b cos x luôn tăng trên R?
A. 1 a + 1 b = 1
B. a + 2 b ≥ 1 + 2 3
C. a 2 + b 2 ≤ 4
D. a + 2 b = 2 3
Tìm mối liên hệ giữa các tham số a và b sao cho hàm số
y
f
(
x
)
2
x
+
a
sin
x
+
b
cos
x
luôn tăng trên
ℝ
A.
1
a
+
1
b
B. a+b
2
3
C. ...
Đọc tiếp
Tìm mối liên hệ giữa các tham số a và b sao cho hàm số y = f ( x ) = 2 x + a sin x + b cos x luôn tăng trên ℝ
A. 1 a + 1 b =
B. a+b= 2 3
C. a 2 + b 2 ≤ 4
D. a+2b ≥ 1 + 2 3
Tìm mối liên hệ giữa các tham số a và b sao cho hàm số yf(x)2x+a.sinx+b.cosx luôn tăng trên R? A.
1
a
+
1
b
1
B.
a
+
2
b
2
3
C.
a
2
+
b
2
≤
4
D....
Đọc tiếp
Tìm mối liên hệ giữa các tham số a và b sao cho hàm số y=f(x)=2x+a.sinx+b.cosx luôn tăng trên R?
A. 1 a + 1 b = 1
B. a + 2 b = 2 3
C. a 2 + b 2 ≤ 4
D. a + 2 b ≥ 1 + 2 3
Tập xác định D=R.
Ta có: y’=2+a.cosx-b.sinx
Áp dụng bất đẳng thức Schwartz ta có 
Yêu cầu của bài toán đưa đến giải bất phương trình
Chọn C.
Đúng 0
Bình luận (0)
cho a = (x+1)/x , b = (y+1)/y , c =( xy+1)/xy
tìm hệ thức liên hệ giữa a,b,c
cho a = (x+1)/x , b = (y+1)/y , c =( xy+1)/xy
tìm hệ thức liên hệ giữa a,b,c
Cho tam giác ABC và trọng tâm M
1) Vẽ đường thẳng d đi qua điểm M cắt cạnh AB, AC Gọi A', B', C' là hình chiếu lần lượt của A, B, C trên d Tìm mối liên hệ giữa AA', BB', CC'
2) Nếu đường thẳng d nằm ngoài tam giác ABC và G' là hình chiếu của G trên d tìm mối liên hệ giữa AA', BB', CC', GG'
Cho tam giác ABC và trọng tâm M
1) Vẽ đường thẳng d đi qua điểm M cắt cạnh AB, AC Gọi A', B', C' là hình chiếu lần lượt của A, B, C trên d Tìm mối liên hệ giữa AA', BB', CC'
2) Nếu đường thẳng d nằm ngoài tam giác ABC và G' là hình chiếu của G trên d tìm mối liên hệ giữa AA', BB', CC', GG'
