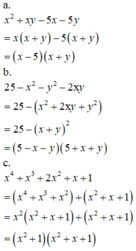a) \(x^4+8x+63\)

\(=x^4+4x^3+9x^2-4x^3-16x^2-36x+7x^2+28x+63\)

\(=x^2\left(x^2+4x+9\right)-4x\left(x^2+4x+9\right)+7\left(x^2+4x+9\right)\)

\(=\left(x^2+4x+9\right)\left(x^2-4x+7\right)\)

c) \(\left(x^2+2x+7\right)+\left(x^2-2x+4\right)\left(x^2+2x+3\right)\left(1\right)\)

Ta có : \(x^3-8=\left(x-2\right)\left(x^2+2x+4\right)\)

\(\Rightarrow x^2+2x+4=\dfrac{x^3-8}{x-2}\)

\(\left(1\right)\Rightarrow\left[\left(\dfrac{x^3-8}{x-2}+3\right)\right]+\left(x^2-2x+4\right)\left[\left(\dfrac{x^3-8}{x-2}-1\right)\right]\)

\(=\left[\left(\dfrac{x^3-3x-14}{x-2}\right)\right]+\left(x^2-2x+4\right)\left[\left(\dfrac{x^3-2x-5}{x-2}\right)\right]\)

\(=\dfrac{1}{x-2}\left[x^3-3x-14+\left(x^2-2x+4\right)\left(x^3-2x-5\right)\right]\)

b: \(\left(x^2+4\right)^2-16x^2\)

\(=\left(x^2-4x+4\right)\left(x^2+4x+4\right)\)

\(=\left(x-2\right)^2\cdot\left(x+2\right)^2\)

c: \(x^5-x^4+x^3-x^2\)

\(=x^4\left(x-1\right)+x^2\left(x-1\right)\)

\(=x^2\left(x-1\right)\left(x^2+1\right)\)

Lời giải:

a. Bạn xem lại đề

b. \((x^2+4)^2-16x^2=(x^2+4)^2-(4x)^2=(x^2+4-4x)(x^2+4+4x)\)

\(=(x-2)^2(x+2)^2\)

c.

\(x^5-x^4+x^3-x^2=x^4(x-1)+x^2(x-1)=(x^4+x^2)(x-1)\)

\(=x^2(x^2+1)(x-1)\)

a) 7x.(-y)+2(y-x)2

=>-7xy+4y-4x

b)(x^2+4)-16x^2

=>x^2+4-16x^2

=>-15x^2+4

c)x^5-x^4+x^3-x^2

=>x^4(x-1)+x^2(x-1)

=>(x^4+x^2)(x-1)

a. $6x^2-11x=x(6x-11)$
b. $x^7+x^5+1=(x^7-x)+(x^5-x^2)+x+x^2+1$

$=x(x^6-1)+x^2(x^3-1)+(x^2+x+1)$
$=x(x^3-1)(x^3+1)+x^2(x^3-1)+(x^2+x+1)$
$=(x^3-1)(x^4+x+x^2)+(x^2+x+1)$

$=(x-1)(x^2+x+1)(x^4+x^2+x)+(x^2+x+1)$
$=(x^2+x+1)[(x-1)(x^4+x^2+x)+1]$

$=(x^2+x+1)(x^5-x^4+x^3-x+1)$

c.

$x^8+x^4+1=(x^4)^2+2.x^4+1-x^4$

$=(x^4+1)^2-(x^2)^2$

$=(x^4+1-x^2)(x^4+1+x^2)$

$=(x^4+1-x^2)(x^4+2x^2+1-x^2)$

$=(x^4-x^2+1)[(x^2+1)^2-x^2]$

$=(x^4-x^2+1)(x^2+1-x)(x^2+1+x)$

d.

$x^3-5x+8-4=x^3-5x+4$

$=x^3-x^2+x^2-x-(4x-4)$

$=x^2(x-1)+x(x-1)-4(x-1)=(x-1)(x^2+x-4)$

e.

$x^5+x^4+1=(x^5-x^2)+(x^4-x)+x^2+x+1$

$=x^2(x^3-1)+x(x^3-1)+x^2+x+1$

$=(x^3-1)(x^2+x)+(x^2+x+1)$
$=(x-1)(x^2+x+1)(x^2+x)+(x^2+x+1)$

$=(x^2+x+1)[(x-1)(x^2+x)+1]$

$=(x^2+x+1)(x^3-x+1)$

a) \(x^2-2x-4y^2-4y=\left(x^2-4y^2\right)-\left(2x+4y\right)=\left(x-2y\right)\left(x+2y\right)-2\left(x+2y\right)=\left(x+2y\right)\left(x-2y-2\right)\)

b) \(x^3+2x^2+2x+1=\left(x+1\right)\left(x^2-x+1\right)+2x\left(x+1\right)=\left(x+1\right)\left(x^2-x+1+2x\right)=\left(x+1\right)\left(x^2+x+1\right)\)

c) \(x^3-4x^2+12x-27=x^3-3x^2-x^2+3x+9x-27=x^2\left(x-3\right)-x\left(x-3\right)+9\left(x-3\right)=\left(x-3\right)\left(x^2-x+9\right)\)

d) \(a^6-a^4+2a^3+2a^2=a^2\left(a^4-a^2+2a+2\right)=a^2\left[a^2\left(a-1\right)\left(a+1\right)+2\left(a+1\right)\right]=a^2\left(a+1\right)\left(a^3-a^2+2\right)=a^2\left(a+1\right)\left[a^3+a^2-2a^2+2\right]=a^2\left(a+1\right)\left[a^2\left(a+1\right)-2\left(a-1\right)\left(a+1\right)\right]=a^2\left(a+1\right)^2\left(a^2-2a+2\right)\)

a) Ta có: \(x^2-2x-4y^2-4y\)

\(=\left(x^2-4y^2\right)-\left(2x+4y\right)\)

\(=\left(x-2y\right)\left(x+2y\right)-2\left(x+2y\right)\)

\(=\left(x+2y\right)\left(x-2y-2\right)\)

b) Ta có: \(x^3+2x^2+2x+1\)

\(=\left(x^3+1\right)+2x\left(x+1\right)\)

\(=\left(x+1\right)\left(x^2-x+1\right)+2x\left(x+1\right)\)

\(=\left(x+1\right)\left(x^2+x+1\right)\)

d) Ta có: \(a^6-a^4+2a^3+2a^2\)

\(=a^2\left(a^4-a^2+2a+2\right)\)

\(=a^2\left[a^2\left(a^2-1\right)+\left(2a+2\right)\right]\)

\(=a^2\left[a^2\left(a-1\right)\left(a+1\right)+2\left(a+1\right)\right]\)

\(=a^2\cdot\left(a+1\right)\left(a^3-a+2\right)\)

c) Ta có: \(x^3-4x^2+12x-27\)

\(=\left(x^3-27\right)-\left(4x^2-12x\right)\)

\(=\left(x-3\right)\left(x^2+3x+9\right)-4x\left(x-3\right)\)

\(=\left(x-3\right)\left(x^2-x+9\right)\)

a,

\(A=4(x-2)(x+1)+(2x-4)^2+(x+1)^2\\=[2(x-2)]^2+2\cdot2(x-2)(x+1)+(x+1)^2\\=[2(x-2)+(x+1)]^2\\=(2x-4+x+1)^2\\=(3x-3)^2\)

Thay $x=\dfrac12$ vào $A$, ta được:

\(A=\Bigg(3\cdot\dfrac12-3\Bigg)^2=\Bigg(\dfrac{-3}{2}\Bigg)^2=\dfrac94\)

Vậy $A=\dfrac94$ khi $x=\dfrac12$.

b,

\(B=x^9-x^7-x^6-x^5+x^4+x^3+x^2-1\\=(x^9-1)-(x^7-x^4)-(x^6-x^3)-(x^5-x^2)\\=[(x^3)^3-1]-x^4(x^3-1)-x^3(x^3-1)-x^2(x^3-1)\\=(x^3-1)(x^6+x^3+1)-x^4(x^3-1)-x^3(x^3-1)-x^2(x^3-1)\\=(x^3-1)(x^6+x^3+1-x^4-x^3-x^2)\\=(x^3-1)(x^6-x^4-x^2+1)\)

Thay $x=1$ vào $B$, ta được:

\(B=(1^3-1)(1^6-1^4-1^2+1)=0\)

Vậy $B=0$ khi $x=1$.

$Toru$

e, x⁴ - 2x³ + x² 

= x²( x²  - 2x + 1)  

= x² (x - 1)²

e: \(x^4-2x^3+x^2\)

\(=x^2\cdot x^2-x^2\cdot2x+x^2\cdot1\)

\(=x^2\left(x^2-2x+1\right)\)

\(=x^2\left(x-1\right)^2\)

f: \(27y^3-x^3\)

\(=\left(3y\right)^3-x^3\)

\(=\left(3y-x\right)\left(9y^2+3xy+x^2\right)\)

a: Ta có: \(x^2-4y^2-2x-4y\)

\(=\left(x-2y\right)\left(x+2y\right)-2\left(x+2y\right)\)

\(=\left(x+2y\right)\left(x-2y-2\right)\)

c: Ta có: \(x^3+2x^2y-x-2y\)

\(=x^2\left(x+2y\right)-\left(x+2y\right)\)

\(=\left(x+2y\right)\left(x-1\right)\left(x+1\right)\)

d: Ta có: \(3x^2-3y^2-2\cdot\left(x-y\right)^2\)

\(=3\left(x-y\right)\left(x+y\right)-2\cdot\left(x-y\right)^2\)

\(=\left(x-y\right)\left(3x+3y-2x+2y\right)\)

\(=\left(x-y\right)\left(x+5y\right)\)

e: Ta có: \(x^3-4x^2-9x+36\)

\(=x^2\left(x-4\right)-9\left(x-4\right)\)

\(=\left(x-4\right)\left(x-3\right)\left(x+3\right)\)

f: Ta có: \(x^2-y^2-2x-2y\)

\(=\left(x-y\right)\left(x+y\right)-2\left(x+y\right)\)

\(=\left(x+y\right)\left(x-y-2\right)\)