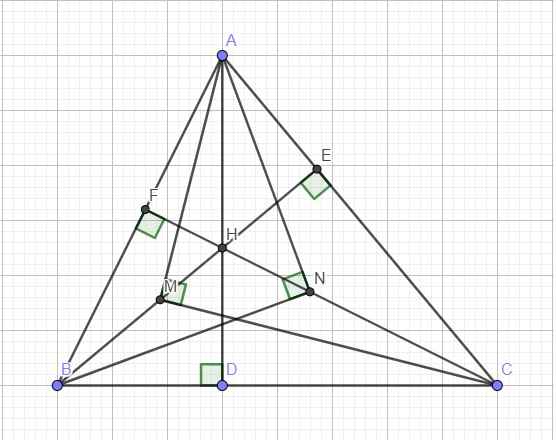
Cho tam giác ABC nhọn có BK và Cl là hai đường cao cắt nhau taị H.Trên đoạn HB lấy điểm E sao cho \(\widehat{AEC=90}\).Trên đoạn HC lấy F sao cho \(\widehat{ÀFB=90}\)CMR tam giác AEF cân tại A

Những câu hỏi liên quan
Cho tam giác ABC có ba góc nhọn, đường cao BK và CL cắt nhau tại H. Trên đọan HB lấy điểm E sao cho góc AEC =90°. Trên đọan HC lấy điểm F sao cho góc AFB =90°. Chứng minh rằng:
a) AK. AC=AL. AB
b) tam giác AEF cân
a) xét tam giác ACL và tam giác AKB, ta có:
GÓC A: chunggóc ALC = góc AKB(=900)=> tam giác ALC ĐỒNG DẠNG tam giác AKB ( g-g)
=> AL = AC
AK AB
=> ALA.AB=AK.AC
B) xét tam giác ABF vuông tại F có đường cao FL, ta có:
AF2= AL.AB (HTL)
XÉT TAM GIÁC AEC VUÔNG TẠI E, CÓ ĐƯỜNG CAO EK, TA CÓ:
AE2 AK.AC ( HTL)
TA CÓ:
AF2= AL.ABAE2= AK.ALAL.AB=AK.AC(CM Ở CÂU A)=> AF=AE
XÉT TAM GIÁC AEF, TA CÓ:
AF=AE(CMT)
=> tam giác AEF cân tại A
Đúng 0
Bình luận (0)
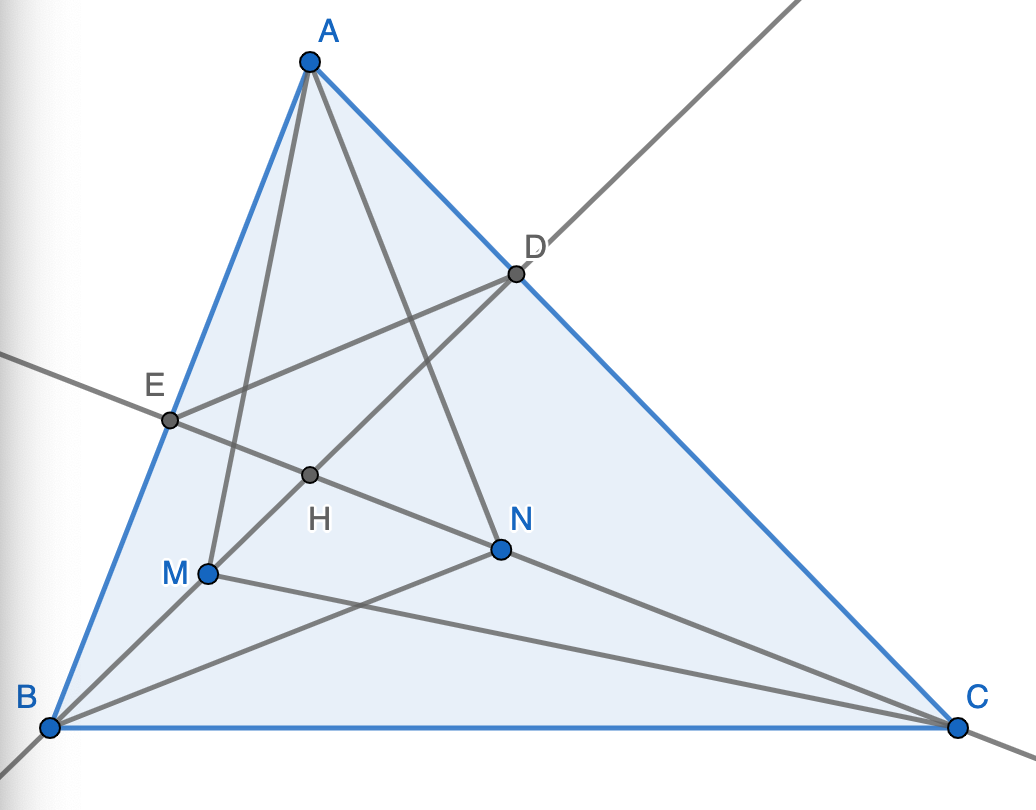
Trên mặt phẳng, cho đoạn thẳng BC=2a(a>0), lấy 1 điểm A bất kì sao cho tam giác ABC nhọn. Các đường cao AD,BR,CF cắt nhau tại H (D,E,F lần lượt nắm trên các cạnh BC, CA, AB). Trên các đoạn HB, HC lần lượt lấy M, N sao cho \(\widehat{AMC}=\widehat{BNA}=90^o\)
a) chứng minh tam giác AMN cân
b) tìm GTLN của BN.CM theo a
Tính chất cơ bản của tam giác với 3 đường cao: \(\Delta AEF\sim\Delta ABC\) (bài toán quen thuộc chắc em tự c/m được)
\(\Rightarrow AF.AB=AE.AC\)
Trong tam giác vuông ABN với đường cao NF:
\(AN^2=AF.AB\)
Trong tam giác vuông ACM:
\(AM^2=AE.AC\)
\(\Rightarrow AM^2=AN^2\Rightarrow AM=AN\)
b. Hệ thức lượng: \(BN^2=BF.AB\) ; \(CM^2=CE.AC\)
\(\Delta ABD\sim\Delta CBF\) (2 tam giác vuông chung góc B)
\(\Rightarrow\dfrac{AB}{BC}=\dfrac{BD}{BF}\Rightarrow BF.AB=BD.BC\) (1)
Hoàn toàn tương tư, \(\Delta ADC\sim\Delta BEC\Rightarrow CE.AC=CD.BC\) (2)
Cộng vế (1) và (2) \(\Rightarrow BF.AB+CE.AC=\left(BD+CD\right)BC=BC^2\)
\(\Rightarrow BN^2+CM^2=BC^2\)
\(\Rightarrow BN.CM\le\dfrac{1}{2}\left(BN^2+CM^2\right)=\dfrac{1}{2}BC^2=2a^2\)
Dấu "=" xảy ra khi tam giác cân tại A
Đúng 2
Bình luận (1)
Cho tam giác nhọn ABC, 2 đường cao BD và CE cắt nhau tại H. Trên HB và HC lần lượt lấy các điểm M và N sao cho \(\widehat{AMC}\) = \(\widehat{ANB}\) = \(90^o\). Chứng minh rằng: AM = AN
Theo đề có: `ΔAMC` là Δ vuông, đường cao `MD`.
=> `AM^2=AD.AC` (1)
`ΔANB` là Δ vuông, đường cao `NE`:
=> `AN^2=AE.AB` (2)
Lại có: `ΔABD=ΔACE`(g.g)
=> \(\dfrac{AB}{AC}=\dfrac{AD}{AE}\Leftrightarrow AB.AE=AC.AD\left(3\right)\)
Từ (1), (2), (3) suy ra: `AM=AD` (đpcm)
$HaNa$
Đúng 4
Bình luận (1)
1. Cho tam giác nhọn ABC hai đường cao BD và CE cắt nhau tại H. M ∈ HB, N ∈ HC sao cho \(\widehat{AMC}=\widehat{ANB}=90^o\). CMR AN=AM
Cho tam giác ABC nhọn có 3 đường cao AH, BK, CI cắt nhau tại M. C/m: a) Tam giác AIK đồng dạng tam giác ACB b) Tam giác MIK đồng dạng tam giác MBC c) AIK AMK AKI AMI ˆ ˆ , ˆ ˆ d) AK.IM + AI.KM = AM.IK e) BM.BK + CM.CI = BC2 f) Trên đoạn thẳng BM và CM lấy các điểm E và F sao cho AEˆC AFˆB 90 . C/m: tam giác AEF cân
Cho tam giác nhọn ABC có các đường cao AD, BE, CF cắt nhau tại H. Lấy điểm M nằm trên đoạn HB, điểm N nằm trên đoạn HC sao cho AMC=ANB=90. Chứng minh:
a, Tam giác AMN cân
b, BC.BD/BF = AC.AE/AF
b) ta có: AE/AF = AB/AC ( câu a )
=) AE×AC/AF= AB (1)
Xét tam giác ADB và tam giác CFB có:
Góc ADB= góc CFB
Chung góc ABC
=) Tam giác ADB đồng dạng với tam giác CFB (g-g)
=) BD/AF= AB/AC
(=) BD×BC/BF= AB (2)
Từ (1) và (2) =) cái đề ( đpcm )
Đúng 0
Bình luận (0)
hình chữ nhật có diện tích 36 cm2, chiều rộng là 3 cm.Hỏi hình chữ nhât đó có chiều dai gấp mấy lần chiều rộng?
Đúng 0
Bình luận (0)
a) Xét tam giác AEB và tam giác AFC có:
Góc AEB = góc AFC
Chung góc BAC
=) Tam giác AEB đồng dạng với tam giác AFC (g-g)
=) AE/AF = AB/AC
(=) AE×AC = AB×AF (1)
Xét tam giác AMC và tam giác AEM có:
Góc AMC= góc AEM
Chung góc MAC
=) Tam giác AMC đồng dạng với tam giác AEM (g-g)
=) AM^2 = AE×AC (2)
Chứng minh tương tự ta có AN^2 = AF×AB (3)
Từ (1); (2) và (3) =) AM^2 = AN^2
Lại có AM và AN là các cạnh của tam giác nên luôn dương
=) AM = AN =) tam giác AMN cân tại A
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
cho tam giác nhọn ABC, các đường cao BD, CE cắt nhau tại H. trên các đoạn HB, HC lấy các điểm M, N sao cho góc AMC = góc ANB = 90 độ. chứng minh:
a) AM= AD.AC
b) Tam giác AMN là tam giác cân
Cho tam giác ABC nhọn, hai đường cao BD và CE cắt nhau tại H. Vẽ hai điểm M và N là hai điểm tương ứng trên các đoạn HB; HC sao cho AMC=ANB=90 độ. CMR: AMN=ANM
Ta có: \(\Delta AMC\) vuông tại M có \(MD\bot AC\Rightarrow AM^2=AD.AC\left(1\right)\)
\(\Delta ANB\) vuông tại Ncó \(NE\bot AB\Rightarrow AN^2=AE.AB\left(2\right)\)
Ta có: \(\angle BEC=\angle BDC=90\Rightarrow BCDE\) nội tiếp \(\Rightarrow\angle ADE=\angle ABC\)
Xét \(\Delta ADE\) và \(\Delta ABC:\) Ta có: \(\left\{{}\begin{matrix}\angle BACchung\\\angle ADE=\angle ABC\end{matrix}\right.\)
\(\Rightarrow\Delta ADE\sim\Delta ABC\left(g-g\right)\Rightarrow\dfrac{AD}{AB}=\dfrac{AE}{AC}\Rightarrow AD.AC=AE.AB\left(3\right)\)
Từ (1),(2) và (3) \(\Rightarrow AM^2=AN^2\Rightarrow AM=AN\Rightarrow\Delta AMN\) cân tại A
\(\Rightarrow\angle AMN=\angle ANM\)

Đúng 2
Bình luận (0)
tam giác ABC nhọn ,các đường cao BI,CK cắt nhau tại H,trên đoạn HB,HC lần lượt lấy các điểm D và E sao cho góc ADC=góc AEB=90 độ
a/ Chứng minh tam giác ADE cân.
b/AD=6cm, AC=10 cm.DC=?, CI=?, diện tích tam giác ADI