Chọn C.

Xét hàm số y = x4- 4x2 - 2

Tính y’ = 4x3 – 8x

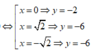
Bảng biến thiên:

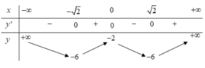
Dựa vào bảng biến thiên suy ra để đồ thị hàm số (C) cắt d tại 4 điểm phân biệt khi và chỉ khi: - 6 < m < -2.

Đáp án A

  y ' = 4 x 3 − 2 mx

Để đồ thị cắt trục hoành tại 4 điểm phân biệt thì đồ thị hàm số phải có 3 cực trị và y C T < 0 < y­­_CĐ Nên m>0 và y’=0 có 3 nghiệm

y ' = 0 ⇔ x= 0 x= 2 m 2 x=- 2 m 2

  y C T < 0 < y­­_CĐ   ⇔ − m 2 4 + m − 1 < 0 < m − 1 ⇔ 2 ≠ m > 1

Đáp án A

  y ' = 4 x 3 − 2 mx

Để đồ thị cắt trục hoành tại 4 điểm phân biệt thì đồ thị hàm số phải có 3 cực trị và y C T < 0 <  y­­_CĐ Nên m > 0  và y’=0 có 3 nghiệm

y ' = 0 ⇔ x= 0 x= 2 m 2 x=- 2 m 2

y C T < 0 < y C Đ ⇔ − m 2 4 + m − 1 < 0 < m − 1 ⇔ 2 ≠ m > 1

+ Phương trình hoành độ giao điểm của (C)  và đường thẳng d:

=x⁴- (2m-1) x²+2m = 2 hay  x⁴- (2m-1) x²+2m -2=0

Suy ra x²= 1 hoặc x²= 2m-2 (1)

+ Đường thẳng d cắt C tại bốn điểm phân biệt có hoành độ nhỏ hơn 3 khi và chỉ khi phương trình (1)  có hai nghiệm phân biệt nhỏ hơn 3.

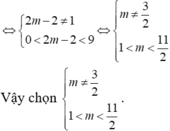
Do đó có 4 giá trị nguyên của m thỏa mãn đầu bài.

Chọn D.

Đáp án D

PT hoành độ giao điểm là: 

Phương trình hoành độ giao điểm của (C)  và đường thẳng d:

1 3 x 3 - m x 2 - x + m + 2 3 = 0 ⇔ ( x - 1 ) x 2 + ( - 3 m + 1 ) x - 3 m - 2 = 0

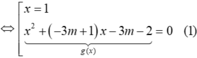
(C) cắt Ox  tại ba điểm phân biệt khi  phương trình (1) có hai nghiệm phân biệt khác 1

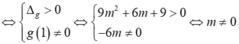
Gọi x₁= 1 còn x₂; x₃ là nghiệm phương trình (1)  nên theo Viet ta có

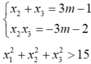
Chọn A.

Phương trình hoành độ giao điểm d và (P):

\(-2x^2=x-m\Leftrightarrow2x^2+x-m=0\) (1)

(d) cắt (P) tại 2 điểm pb khi (1) có 2 nghiệm pb

\(\Leftrightarrow\Delta=1+8m>0\Leftrightarrow m< -\dfrac{1}{8}\)

Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{1}{2}\\x_1x_2=-\dfrac{m}{2}\end{matrix}\right.\)

\(x_1+x_2=x_1x_2\Leftrightarrow-\dfrac{1}{2}=-\dfrac{m}{2}\Leftrightarrow m=1\)

PTHĐGĐ là;

x^2-3x-m^2+1=0

Δ=(-3)^2-4(-m^2+1)=4m^2-4+9=4m^2+5>0

=>Phương trình luôn có hai nghiệm phân biệt

TH1: x1>0; x2>0

=>x1+2x2=3

mà x1+x2=3

nên x1=1; x2=1

x1*x2=-m^2+1

=>-m^2+1=1

=>m=0

TH2: x1<0; x2>0

=>-x1+2x2=3 và x1+x2=3

=>x1=1; x2=2

x1*x2=-m^2+1

=>-m^2+1=2

=>-m^2-1=0(loại)

TH2: x1>0; x2<0

=>x1-2x2=0 va x1+x2=3

=>x1=2 và x2=1

x1*x2=-m^2+1

=>-m^2+1=2

=>-m^2=1(loại)

TH3: x1<0; x2<0

=>-x1-2x2=3 và x1+x2=3

=>x1=9 và x2=-6

x1*x2=-m^2+1

=>-m^2+1=-54

=>-m^2=-55

=>\(m=\pm\sqrt{55}\)

Hoành độ giao điểm tm pt 

\(x^2-mx+3=0\)

\(\Delta=m^2-4.3=m^2-12\)

Để pt có 2 nghiệm pb khi m^2 - 12 > 0 

Theo Vi et \(\left\{{}\begin{matrix}x_1+x_2=m\\x_1x_2=3\end{matrix}\right.\)

Ta có \(\left(x_1+x_2\right)^2-2x_1x_2-2\left|x_1x_2\right|=4\)

Thay vào ta được \(m^2-6-2.3=4\Leftrightarrow m^2-16=0\Leftrightarrow m=4;m=-4\)(tm)