Cho tam giác MNP nội tiếp (O) có góc M< góc N< góc P. Gọi OH, OK, OI lần lượt là khoảng cách từ O đến MN, NP, MP. So sánh OH, OK, OI
Những câu hỏi liên quan
cho tam giác mnp có M>N>P nội tiếp đường tròn ()O. Gọi OH, OI, OKtheo thứtựlà khoảng cách từOđến MN, NP, MP. So sánh các độdài OH, OIvà OK.
Cho tam giác MNP với các góc nhọn và MN<MP. Trên cạnh MP lấy điểm Psao cho MD=MN. Vẽ đường tròn (O) ngoại tiếp tam giác NDP
a) So sánh các cung nhỏ PD, DN, PN
b)Từ O kẻ OI,OH,OK lần lượt vuông góc với PN,ND,PD,So sánh các đoạn OI,OH,OK
Cho tam giác ABC nội tiếp đường tròn (O) có góc A>góc B >gócC .Gọi OH,OI,OK theo thứ tự là khoảng cách từ O đến BC,AC,AB.So sánh độ dài OH,OI,OK
Tam giác ABC có ˆA>ˆB>ˆCA^>B^>C^ nên suy ra:
BC > AC > AB (cạnh đối diện góc lớn hơn thì lớn hơn)
Ta có AB, BC, AC lần lượt là các dây cung của đường tròn (O)
Mà BC < AC > AB nên suy ra:
OH < OI < OK ( dây lớn hơn gần tâm hơn).
Chúc bạn học tốt !!!
Đúng 1
Bình luận (0)
3 tháng 12 2023 lúc 10:19
cho tm giác ABC nội tiếp đường tòn tâm O, có góc A>B>C. gọi OH,OI,OK là khoảng cách từ tâm đến BC, AC,AB. so sánh OH,OI,OK;
Xét ΔABC có \(\widehat{BAC}>\widehat{ABC}>\widehat{ACB}\)
mà BC là cạnh đối diện của góc BAC
và AC là cạnh đối diện của góc ABC
và AB là cạnh đối diện của góc ACB
nên BC>AC>AB
Xét (O) có
BC,AC,AB là các dây
BC>AC>AB
OH,OI,OK lần lượt là khoảng cách từ tâm O đến các dây BC,AC,AB
Do đó: OH<OI<OK
Đúng 1
Bình luận (0)
Tam giác ABC nội tiếp đường tròn (O) có ∠ A > ∠ B > ∠ C. Gọi OH, OI, OK theo thứ tự là khoảng cách từ O đến BC, AC, AB. So sánh các độ dài OH, OI, OK.
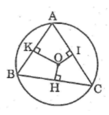
Tam giác ABC có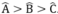 
nên suy ra :
BC > AC > AB (cạnh đối diện góc lớn hơn thì lớn hơn)
Ta có AB, BC, AC lần lượt là các dây cung của đường tròn (O)
Mà BC > AC > AB nên suy ra:
OH < OI < OK (dây lớn hơn gần tâm hơn)
Đúng 0
Bình luận (0)
Tam giác ABC nội tiếp đường tròn (O) có \(\widehat{A}>\widehat{B}>\widehat{C}\). Gọi OH, OI, OK theo thứ tự là khoảng cách từ O đến BC, AC, AB. So sánh các độ dài OH, OI, OK ?
Ta có \(\widehat{A}>\widehat{B}>\widehat{C}\) nên \(BC>AC>AB\)
Do đó \(OH< OI< OK\)
Đúng 0
Bình luận (0)
Cho tam giác MNP có MN = MP.Gọi O là trung điểm của NP
a) CMR MO vuông góc với NP
b) Kẻ OH vuông góc vơi MN;OK vuông góc với MP
CMR MH = MK;OK vuông góc với MP
Cho tam giác ABC,M là trung điểm của BC.Trên tia đối của tia MA lấy điểm E sao cho ME = MA
CMR:a)Tam giác ABM = Tam giác ECM
b)AB song song với CE
Đúng 0
Bình luận (0)
ở bài tam giácMNP:
a,đầu tiên hãy chứng minh rằng tam giácMON =tam giácMOP(g.c.g)
suy ra góc MON bắng góc MOP,suy ra MON=MOP=90độ
vậy MO vuông góc với NP
Đúng 0
Bình luận (0)
b,chứng minh tam giác đó bằng nhau theo trường hợp cạnh huyền góc nhọn
suy ra MH=MK(hai cạnh tương ứng)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho tam giác đều ABC, từ điểm O bất kì trong tam giác ABC vẽ OH vuông góc với AB,OK vuông góc với AC, OI vuông góc với BC. Chứng minh rằng OH+OK+OI không đổi khi O di động trong tam giác ABC
cho tam giác ABC nội tiếp đường tròn tâm O. Biết A=50 độ, B=65 độ. Kẻ OH vuông AB, OI vuông AC, OK vuông BC. So sánh OH, OK, OI
