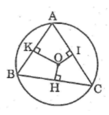
Tam giác ABC có 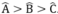 nên suy ra :
nên suy ra :
BC > AC > AB (cạnh đối diện góc lớn hơn thì lớn hơn)
Ta có AB, BC, AC lần lượt là các dây cung của đường tròn (O)
Mà BC > AC > AB nên suy ra:
OH < OI < OK (dây lớn hơn gần tâm hơn)

Tam giác ABC có 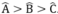 nên suy ra :
nên suy ra :
BC > AC > AB (cạnh đối diện góc lớn hơn thì lớn hơn)
Ta có AB, BC, AC lần lượt là các dây cung của đường tròn (O)
Mà BC > AC > AB nên suy ra:
OH < OI < OK (dây lớn hơn gần tâm hơn)
Cho tam giác ABC nội tiếp đường tròn (O) có góc A>góc B >gócC .Gọi OH,OI,OK theo thứ tự là khoảng cách từ O đến BC,AC,AB.So sánh độ dài OH,OI,OK
cho tm giác ABC nội tiếp đường tòn tâm O, có góc A>B>C. gọi OH,OI,OK là khoảng cách từ tâm đến BC, AC,AB. so sánh OH,OI,OK;
cho tam giác ABC có AB=AC=40, BC=48. gọi O và I thứ tự là tâm đường tròn ngoại tiếp tam và nội tiếp tam giác. tính
a) Bán kính đường tròn nội tiếp
b) Bán kính đường tròn ngoại tiếp
c) Khoảng cách OI
Cho tam giác MNP với các góc nhọn và MN<MP. Trên cạnh MP lấy điểm Psao cho MD=MN. Vẽ đường tròn (O) ngoại tiếp tam giác NDP
a) So sánh các cung nhỏ PD, DN, PN
b)Từ O kẻ OI,OH,OK lần lượt vuông góc với PN,ND,PD,So sánh các đoạn OI,OH,OK
Cho tam giác ABC . Trên tia đối của tia AB lấy một điểm D sao cho AD = AC. Vẽ đường tròn tâm O ngoại tiếp tam giác DBC. Từ O lần lượt hạ các đường vuông góc OH, OK với BC và BD (H ∈ BC, K ∈ BD)
a) Chứng minh rằng OH > OK.
b) So sánh hai cung nhỏ BD và BC.
Cho tam giác ABC nội tiếp đường tròn tâm O, đường phân giác AD. Gọi H, K theo thứ tự là tâm của các đường tròn ngoại tiếp các tam giác ABD, ACD. Chứng minh rằng OH = OK.
Cho tam giác ABC cân nội tiếp đường tròn (O;R) có độ dài cạnh AB=AC=R ( BC khác đường kính)
a) Cm AO là tia phân giác của góc BAC
b) Cm BC > AB suy ra thứ tự khoảng cách từ tâm O đến các cạnh của tam giác ABC
c) Tính BC theo R chiều cao hạ từ A và diện tích tam giác ABC
Cho tam giác đều ABC, từ điểm O bất kì trong tam giác ABC vẽ OH vuông góc với AB,OK vuông góc với AC, OI vuông góc với BC. Chứng minh rằng OH+OK+OI không đổi khi O di động trong tam giác ABC
Cho tam giác ABC có AB > AC .Trên cạnh AB lấy điểm D sao cho AD = AC đường tròn tâm O ngoại tiếp tam giác BCD .Từ O lần lượt hạ các đường vuông góc OH,OK xuống BC và BD (H ∈ BC , K ∈ BD). So sánh hai cung nhỏ BD và BC