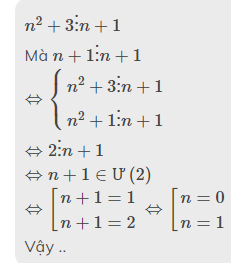a)4n-7chia hết cho n-1<=>4(n-1)-3chia hết cho n-1=>3chia hết cho n-1 mà n thuộc N

=>n-1 thuộc{-1;1;3}

=>n thuộc {1;2;4}

b)10-2n chia hết cho n-2<=>14-2(n-2) chia hết cho n-2 =>14 chia hết cho n-2 mà n thuộc N

=>n-2 thuộc {-2;-1;1;2;7;14}

=>n thuộc {0;1;3;4;9;16}

c)5n-8 chia hết cho 4-n <=>5(4-n)-28 chia hết cho n-4=>28chia hết cho n-4 mà n thuộc N

=>n-4 thuộc {-4;-2;-1;1;2;4;7;14;28}

=>n thuộc{0;2;3;5;6;8;11;18;32}

d)n²+3n+6 chia hết cho n-3<=>-n(n-3)+6 chia hết cho n-3=>6 chia hết cho n-3 mà n thuộc N

=>n-3 thuộc{-3;-2;-1;1;2;3;6}

=>n thuộc{0;1;2;4;5;6;9}

Sai hêta rồi bạn ơi

Đúng ko bạn hiền 

Có: 1n + 2n + 3n + 4n

= (1 + 2 + 3 + 4)n

= 10n

Vì 10 ⋮ 5 nên 10n ⋮ 5 (n ∈ N)

Vậy để 1n + 2n + 3n + 4n chia hết cho 5 thì n ∈ N.

Để 1n + 2n + 3n + 4n chia hết cho 5, ta cần tìm số tự nhiên n sao cho tổng này chia hết cho 5.

Ta có: 1n + 2n + 3n + 4n = 10n

Để 10n chia hết cho 5, ta cần n chia hết cho 5.

Vậy, số tự nhiên n cần tìm là các số chia hết cho 5.

 ⇒ Các số tự nhiên n chia hết cho 5.

--thodagbun--

quá là ez 

đáp án là 5

Vì 1n = 1.5 = 5 : 5 = 1

2N = 2.5 = 10:5 = 2

Tương tự

11:

n^3-n^2+2n+7 chia hết cho n^2+1

=>n^3+n-n^2-1+n+8 chia hết cho n^2+1

=>n+8 chia hết cho n^2+1

=>(n+8)(n-8) chia hết cho n^2+1

=>n^2-64 chia hết cho n^2+1

=>n^2+1-65 chia hết cho n^2+1

=>n^2+1 thuộc Ư(65)

=>n^2+1 thuộc {1;5;13;65}

=>n^2 thuộc {0;4;12;64}

mà n là số tự nhiên

nên n thuộc {0;2;8}

Thử lại, ta sẽ thấy n=8 không thỏa mãn

=>\(n\in\left\{0;2\right\}\)

Lời giải:
$A=1^n+2^n+3^n+4^n=1+2^n+3^n+4^n$

Nếu $n=4k$ thì:

$A=1+2^n+3^n+4^n=1+2^{4k}+3^{4k}+4^{4k}$

$=1+16^k+81^k+16^{2k}$

$\equiv 1+1+1+1\equiv 4\pmod 5$

---------------

Nếu $n=4k+1$

$A=1+2^n+3^n+4^n=1+2^{4k+1}+3^{4k+1}+4^{4k+1}$

$=1+16^k.2+81^k.3+16^{2k}.4$

$\equiv 1+1^k.2+1^k.3+1^k.4\equiv 10\equiv 0\pmod 5$

Nếu $n=4k+2$

$A=1+2^n+3^n+4^n=1+2^{4k+2}+3^{4k+2}+4^{4k+2}$

$=1+16^k.2^2+81^k.3^2+16^{2k}.4^2$

$\equiv 1+1^k.2^2+1^k.3^2+1^{2k}.4^2\equiv 30\equiv 0\pmod 5$

Nếu $n=4k+3$

$A=1+2^n+3^n+4^n=1+2^{4k+3}+3^{4k+3}+4^{4k+3}$

$=1+16^k.2^3+81^k.3^3+16^{2k}.4^3$

$\equiv 1+1^k.2^3+1^k.3^3+1^{2k}.4^3\equiv 100\equiv 0\pmod 5$

Vậy chỉ cần $n$ không chia hết cho $4$ thì $1^n+2^n+3^n+4^n$ sẽ chia hết cho $5$

a) \(\frac{4n+3}{2n+1}=\frac{4n+2+1}{2n+1}=2+\frac{1}{2n+1}\)

Để có phép chia hết thì \(1⋮2n+1\Leftrightarrow2n+1\inƯ\left(1\right)=\left\{\pm1\right\}\)

b) \(\frac{3n-5}{4n+8}=\frac{3n+6-11}{4n+8}=\frac{3}{4}-\frac{11}{4n+8}\)

Để có phép chia hết thì \(11⋮4n+8\Leftrightarrow4n+8\inƯ\left(11\right)=\left\{\pm1;\pm11\right\}\)

c) \(\frac{n+3}{n-1}=\frac{n-1+4}{n-1}=1+\frac{4}{n-1}\)

Để có phép chia hết thì \(4⋮n-1\Leftrightarrow n-1\inƯ\left(4\right)=\left\{\pm1;\pm2;\pm4\right\}\)

d) \(\frac{3n+1}{11-n}=\frac{3n-33+34}{11-n}=-1+\frac{34}{11-n}\)

Để có phép chia hết thì \(34⋮11-n\Leftrightarrow11-n\inƯ\left(34\right)=\left\{\pm1;\pm2;\pm17;\pm34\right\}\)

Lập bảng xét giá trị cho từng trường hợp

a, 

Ta có: 4n-5 chia hết cho 2n-1

=>4n-2-3 chia hết cho 2n-1

=>2.(2n-1)-3 chia hết cho 2n-1

=>3 chia hết cho 2n-1

=>2n-1=Ư(3)=(-1,-3,1,3)

=>2n=(0,-2,2,4)

=>n=(0,-1,1,2)

Vậy n=0,-1,1,2

b,