Cho tam giác ABC có AB=AC . Tia phân giác góc A cắt BC tại D . 

a, Chứng minh tam giác ABD bằng tam giác ACD .

b , Trên nửa mặt phẳng bờ BC chứa điểm A vẽ tia Cx vuông góc BC . Trên nửa mặt phẳng bờ chứa AB  chứa điểm C vẽ tia AY song song BC . Chứng minh góc yAc = góc ABC .

c , Chứng minh AD song song Cx 

d, Gọi I là trung điểm của AC , K là giao điểm của 2 tia Ay và Cx . Chứng minh I là trung điểm của DK . 

Nhờ các bạn giải dùm mình câu cuối 3 bài này nhé! Thanks các bạn!

Bài 1: Cho Hình chữ nhật ABCD có O là giao điểm hai đường chéo, E nằm giữa O và B. Điểm F đối xứng với A qua E, I là trung điểm của CF.

a) CM: OEFC là hình thang

b) CM: OEIC là hình bình hành.

c) Gọi H và K lần lượt là hình chiếu của F lên BC và CD. CM: CHFK là hình chữ nhật. 

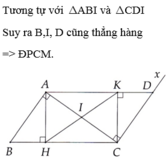
d) CM: E, H, K thẳng hàng. (nhờ mọi người làm giúp câu này)

Bài 2: Cho tam giác ABC vuông tại A (AB>AC). Đường cao AH, gọi M là trung điểm AC. Trên tia đối của tia MH lấy điểm D sao cho MD=MH.

a) CM: ADCH là hình chữ nhật.

b) Gọi E là điểm đối xứng với C qua H. CM: ADHE là hình bình hành.

c) Vẽ EK vuông góc với AB tại K. I là trung điểm AK. CM: KE // IH.

d) Gọi N là trung điểm BE. CM: HK vuông góc với KN. (nhờ mọi người làm giúp câu này)

Bài 3: Cho tam giác ABC nhọn, AH là đường cao. Qua A vẽ đường thẳng vuông góc với AH và qua B vẽ đường thẳng vuông góc với BC, hai đường này cắt nhau tại E.

a) Vẽ đường cao BK của tam giác ABC cắt AH tại N. Gọi F là điểm đối xứng của B qua K mà M là điểm đối xứng của A qua K. CM ABMF là hình thoi.

b) Gọi D và I lần lượt là trung điểm của AC và BC. hai đường trung trực của AC và BC cắt nhau tại O. Gọi L là điểm đối xứng với A qua O. CM: LC // BN.

c) CM: N, I, L thẳng hàng. (nhờ mọi người làm giúp câu này)

Cho tam giác ABC vuông tại A (AB<AC),trung tuyến AO.Điểm D là điểm đối xứng với A qua O.

a) Chứng minh tứ giác ABDC là hình chữ nhật.

b) Vẽ đường cao AH của tam giác ABC.Trên tia đối của tia HA lấy điểm K sao cho HK=HA.

    Chứng minh BKDC là hình thang cân.

c) M là trung điểm của AC.Lấy E đối xứng với O qua M.Hỏi AECO là hình gì? Vì sao?

d) Trên nửa mặt phẳng bờ BC có chứa điểm A vẽ BF⊥BC và BF=AH.

     Chứng minh: S_BKD+S_AFBH+S_AOCE=S_ABDC.

Cho tam giác ABC vuông tại A có B ^ =   55 ° . Trên nửa mặt phẳng bờ AC không chứa B, vẽ tia Cx vuông góc với AC. Trên tia Cx lấy điểm D sao cho CD = AB.

a) Tính số đo  A C B ^

b) Chứng minh ∆ A B C   =   ∆ C D A  và AD//BC.

c) Kẻ A H ⊥   B C   ( H ∈   B C ) và C K ⊥   A D   ( K   ∈   A D ) . Chứng minh BH = DK.

d) Gọi I là trung điểm của AC. Chứng minh ba điểm H, I, K thẳng hàng và 3 đường thẳng AC, HK, BD cùng gặp nhau ở I.