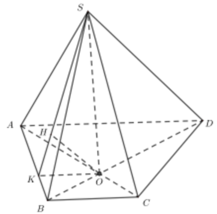
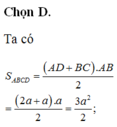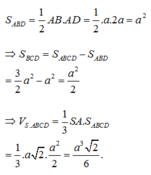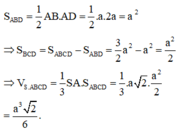Cho hình chóp S.ABCD có đáy ABCD là hính thang vuông tại A và B AB=BC=a , SA =a và vuông góc với mặt phẳng (ABCD) .Khoảng cách từ D đến mặt phẳng (SAC) bằng a√2. Tính thể tích V S.ABCD
Những câu hỏi liên quan
Cho hình chóp S.ABCD có đáy ABCD là hính thang vuông tại A và B AB=BC=a , SA =a và vuông góc với mặt phẳng (ABCD) .Khoảng cách từ D đến mặt phẳng (SAC) bằng a√2. Tính thể tích V S.ABCD
1 tháng 6 2021 lúc 16:42
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B có AD=3a, AB=BC=2a. Biết SA⊥(ABCD).
a) Tính khoảng cách từ C đến mặt phẳng (SAD).
b) Tính khoảng cách từ D đến mặt phẳng(SAC).
a, Ta có: \(\left\{{}\begin{matrix}AB\perp SA\left(do:SA\perp\left(ABCD\right)\right)\\AB\perp AD\left(gt\right)\end{matrix}\right.\)
\(\Rightarrow AB\perp\left(SAD\right)\)
Từ C kẻ CH // AB ⇒ CH ⊥ (SAD)
⇒ d (C, (SAD)) = CH = 2a
b, Ta có: \(\left(SAC\right)\cap\left(ABCD\right)=AC\)
Hạ DE ⊥ AC ⇒ DE ⊥ (SAC)
⇒ d(D, (SAC)) = DE
Ta có: AC = 2a√2, AH = HC 2a và HD = a
Xét tam giác HDC vuông tại H, có: \(DC=\sqrt{HD^2+HC^2}=a\sqrt{5}\)
Xét tam giác AHC vuông cân tại H, có: \(\widehat{HAC}=45^o=\widehat{DAE}\)
Xét tam giác ADE vuông tại E, có: \(DE=AD.sin\widehat{DAE}=\dfrac{3a\sqrt{2}}{2}\)
Đúng 2
Bình luận (0)
SGK Kết nối tri thức và cuộc sống
16 tháng 8 2023 lúc 18:34
Cho hình chóp S.ABCD có đáy ABCD là hình thang cân, \(AB//CD\) và \(AB = BC = DA = a\), \(CD = 2a\). Biết hai mặt phẳng \((SAC)\) và \((SBD)\) cùng vuông góc với mặt phẳng đáy \((ABCD)\) và \(SA = a\sqrt 2 \). Tính theo \(a\) khoảng cách từ \(S\) đến mặt phẳng \((ABCD)\) và thể tích của khối chóp S.ABCD.
Xét mặt phẳng đáy (ABCD) là hình thang cân. Kéo dài AC cắt BD tại I ta thu được tam giác đều ICD.
Do đó AD và BC đồng thời là đường cao và là đường trung tuyến của tam giác ICD. Suy ra O là trọng tâm của tam giác ICD (Với O là giao của AD và BC)
Ta có: \(AD=\sqrt{CD^2-AC^2}=a\sqrt{3}\)
\(\Rightarrow OA=\dfrac{1}{3}a\sqrt{3}\)
Vì hai mặt phẳng (SAC) và (SBD) cùng vuông góc với mặt phẳng đáy (ABCD) và có giao tuyến là SO. Do đó SO vuông góc với (ABCD)
Xét tam giác SOB vuông tại O ta có:
\(SO=\sqrt{SA^2-OA^2}=\dfrac{\sqrt{15}}{3}a\)
Vậy khoảng cách từ S đến mặt phẳng (ABCD) là \(\dfrac{\sqrt{15}}{3}a\)
Ta có: \(S_{ABCD}=\dfrac{3}{4}.S_{ICD}=\dfrac{3}{4}.\dfrac{AD.CI}{2}=\dfrac{3}{8}.a\sqrt{3}.2a=\dfrac{3\sqrt{3}}{4}a^2\)
\(\Rightarrow V_{S.ABCD}=\dfrac{1}{3}.SO.S_{ABCD}=\dfrac{1}{3}.\dfrac{\sqrt{15}}{3}a.\dfrac{3\sqrt{3}}{4}a^2=\dfrac{\sqrt{5}}{4}a^3\)
Đúng 1
Bình luận (0)
SGK Kết nối tri thức và cuộc sống
16 tháng 8 2023 lúc 18:34
Cho hình chóp S.ABCD có đáy ABCD là hình thang cân, \(AB//CD\) và \(AB = BC = DA = a\), \(CD = 2a\). Biết hai mặt phẳng \((SAC)\) và \((SBD)\) cùng vuông góc với mặt phẳng đáy \((ABCD)\) và \(SA = a\sqrt 2 \). Tính theo \(a\) khoảng cách từ \(S\) đến mặt phẳng \((ABCD)\) và thể tích của khối chóp S.ABCD.
Xét mặt phẳng đáy (ABCD) là hình thang cân. Kéo dài AC cắt BD tại I ta thu được tam giác đều ICD.
Do đó AD và BC đồng thời là đường cao và là đường trung tuyến của tam giác ICD. Suy ra O là trọng tâm của tam giác ICD (Với O là giao của AD và BC)
Ta có: \(AD=\sqrt{CD^2-AC^2}=a\sqrt{3}\)
\(\Rightarrow OA=\dfrac{1}{3}a\sqrt{3}\)
Vì hai mặt phẳng (SAC) và (SBD) cùng vuông góc với mặt phẳng đáy (ABCD) và có giao tuyến là SO. Do đó SO vuông góc với (ABCD)
Xét tam giác SOB vuông tại O ta có:
\(SO=\sqrt{SA^2-OA^2}=\dfrac{\sqrt{15}}{3}a\)
Vậy khoảng cách từ S đến mặt phẳng (ABCD) là \(\dfrac{\sqrt{15}}{3}a\)
Ta có: \(S_{ABCD}=\dfrac{3}{4}.S_{ICD}=\dfrac{3}{4}.\dfrac{AD.CI}{2}=\dfrac{3}{8}.a\sqrt{3}.2a=\dfrac{3\sqrt{3}}{4}a^2\)
\(\Rightarrow V_{S.ABCD}=\dfrac{1}{3}.SO.S_{ABCD}=\dfrac{1}{3}.\dfrac{\sqrt{15}}{3}a.\dfrac{3\sqrt{3}}{4}a^2=\dfrac{\sqrt{5}}{4}a^3\)
Đúng 1
Bình luận (0)
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B;
A
B
B
C
1
,
A
D
2.
Các mặt chéo
S
A
C
và
S
B
D
cùng vuông góc với mặt đáy
A
B
C
D...
Đọc tiếp
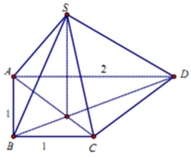
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B; A B = B C = 1 , A D = 2. Các mặt chéo S A C và S B D cùng vuông góc với mặt đáy A B C D . Biết góc giữa hai mặt phẳng S A B và A B C D bằng 60 0 (tham khảo hình vẽ bên). Khoảng cách từ điểm D đến mặt phẳng S A B là
A. 2 3 3
B. 3
C. 2 3
D. 3 3
Câu 1: Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B, với AB=BC=a ; AD=2a. Các mặt phẳng (SAC) và (SBD) cùng vuông góc với mặt đáy ( ABCD). Biết góc giữa hai mặt phẳng ( SAB) và ( ABCD) bằng 60 độ. Tính thể tích khối chóp và khoảng cách giữa hai đường thẳng CD và SB.
Cho hình chóp S.ABCD có đường thẳng SA vuông góc với mặt phẳng (ABCD), đáy ABCD là hình thang vuông tại A và B, có
A
B
a
,
A
D
2
a
,
B
C
a
. Biết rằng
S
A
a
2
. Tính thể tích V của khối chóp S.ABCD theo a.
Đọc tiếp
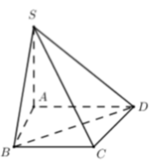
Cho hình chóp S.ABCD có đường thẳng SA vuông góc với mặt phẳng (ABCD), đáy ABCD là hình thang vuông tại A và B, có A B = a , A D = 2 a , B C = a . Biết rằng S A = a 2 . Tính thể tích V của khối chóp S.ABCD theo a.
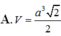
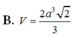
Cho hình chóp S.ABCD có đường thẳng SA vuông góc với mặt phẳng (ABCD), đáy ABCD là hình thang vuông tại A và B, có
A
B
a
,
A
D
2
a
,
B
C
a
.
Biết rằng
S
A
a
2
Tính thể tích V của khối chóp S.ABCD theo a. A.
V
a
3...
Đọc tiếp
Cho hình chóp S.ABCD có đường thẳng SA vuông góc với mặt phẳng (ABCD), đáy ABCD là hình thang vuông tại A và B, có A B = a , A D = 2 a , B C = a . Biết rằng S A = a 2 Tính thể tích V của khối chóp S.ABCD theo a.
A. V = a 3 2 2
B. V = 2 a 3 2 3
C. V = 2 a 2 3
D. V = a 3 2 6
Hình chóp S.ABCD có đáy là hình thang vuông ABCD vuông tại A và D, có AB 2a, AD DC a, có cạnh SA vuông góc với mặt phẳng (ABCD) và SA a.a) Chứng minh mặt phẳng (SAD) vuông góc với mặt phẳng (SDC), mặt phẳng (SAC) vuông góc với mặt phẳng (SCB).b) Gọi φ là góc giữa hai mặt phẳng (SBC) và (ABCD), tính tanφ.c) Gọi (α) là mặt phẳng chứa SD và vuông góc với mặt phẳng (SAC). Hãy xác định (α) và xác định thiết diện của hình chóp S.ABCD với (α)
Đọc tiếp
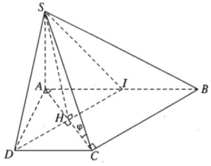
Hình chóp S.ABCD có đáy là hình thang vuông ABCD vuông tại A và D, có AB = 2a, AD = DC = a, có cạnh SA vuông góc với mặt phẳng (ABCD) và SA = a.
a) Chứng minh mặt phẳng (SAD) vuông góc với mặt phẳng (SDC), mặt phẳng (SAC) vuông góc với mặt phẳng (SCB).
b) Gọi φ là góc giữa hai mặt phẳng (SBC) và (ABCD), tính tanφ.
c) Gọi (α) là mặt phẳng chứa SD và vuông góc với mặt phẳng (SAC). Hãy xác định (α) và xác định thiết diện của hình chóp S.ABCD với (α)
a) Ta có:
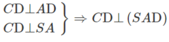
⇒ (SCD) ⊥ (SAD)
Gọi I là trung điểm của đoạn AB. Ta có AICD là hình vuông và IBCD là hình bình hành. Vì DI // CB và DI ⊥ CA nên AC ⊥ CB. Do đó CB ⊥ (SAC).
Vậy (SBC) ⊥ (SAC).
b) Ta có:
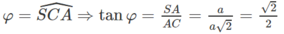
c)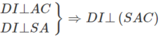 
Vậy (α) là mặt phẳng chứa SD và vuông góc với mặt phẳng (SAC) chính là mặt phẳng (SDI). Do đó thiết diện của (α) với hình chóp S.ABCD là tam giác đều SDI có chiều dài mỗi cạnh bằng a√2. Gọi H là tâm hình vuông AICD ta có SH ⊥ DI và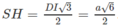 
.
Tam giác SDI có diện tích:
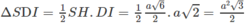
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy là hình thoi ABCD cạnh a, có góc
B
A
D
^
60
o
và
S
A
S
B
S
D
a
3
2
a) Tính khoảng cách từ S đến mặt...
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình thoi ABCD cạnh a, có góc B A D ^ = 60 o và S A = S B = S D = a 3 2
a) Tính khoảng cách từ S đến mặt phẳng (ABCD) và độ dài cạnh SC.
b) Chứng minh mặt phẳng (SAC) vuông góc với mặt phẳng (ABCD).
c) Chứng minh SB vuông góc với BC.
d) Gọi φ là góc giữa hai mặt phẳng (SBD) và (ABCD). Tính tanφ.
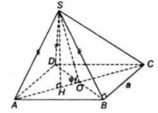
a) Tam giác ABD có AB = AD ( do ABCD là hình thoi)
=> Tam giác ABD cân tại A. Lại có góc A= 60o
=> Tam giác ABD đều.
Lại có; SA = SB = SD nên hình chóp S.ABD là hình chóp đều.
* Gọi H là tâm của tam giác ABD
=>SH ⊥ (ABD)
*Gọi O là giao điểm của AC và BD.
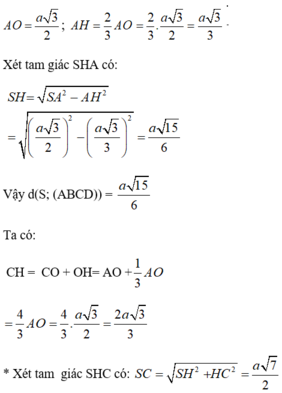
Đúng 0
Bình luận (0)