Cho tứ giác ABCD nội tiếp (O) có AB < CD, AC < BC. AB cắt CD tại M, AC cắt BD tại N. Tia phân giác của \(\widehat{AMC}\) và \(\widehat{ANB}\) cắt nhau tại I. Chứng minh: I thuộc đường tròn có đường kính MN

Những câu hỏi liên quan
Cho tứ giác ABDC có A,B,C,D thuộc đường tròn tâm O;có AB<CD;AC<BD,AB cắt CD tại M,AC cắt BD tại N,tia phân giác góc AMC cắt tia phân giác góc ANB tại I. cmr: I thuộc đường tròn đường kính MN
Cho tứ giác ABCD nội tiếp đường tròn (O) có AB = BD. Các đường thẳng AB và DC cắt nhau tại N, đường thẳng CB cắt tiếp tuyến tại A của đường tròn (O) tại M. Chứng minh \(\widehat{AMN}=\widehat{ABD}\)
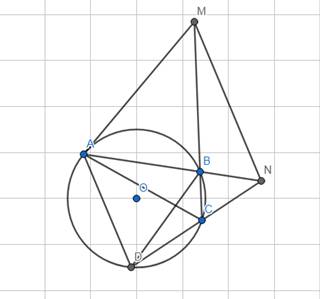
*Chứng minh AMNC là tứ giác nội tiếp.
Ta có AB=BD nên △ABD cân tại B.
\(\Rightarrow\widehat{ADB}=\widehat{BAD}\left(1\right)\)
Trong (O) có: \(\widehat{MAB}\) là góc tạo bởi tiếp tuyến và dây cung chắn cung AB.
\(\widehat{ADB}\) là góc nội tiếp chắn cung AB.
\(\Rightarrow\widehat{MAB}=\widehat{ADB}\left(2\right)\)
Tứ giác ABCD nội tiếp có \(\widehat{BCN}\) là góc ngoài ở đỉnh C.
\(\Rightarrow\widehat{BCN}=\widehat{BAD}\left(3\right)\)
(1), (2), (3) \(\Rightarrow\widehat{MAB}=\widehat{BCN}\).
\(\Rightarrow\)AMNC nội tiếp.
*Chứng minh yêu cầu đề bài.
AMNC nội tiếp \(\Rightarrow\widehat{AMN}=\widehat{ACD}\) (\(\widehat{ACD}\) là góc ngoài ở đỉnh C).
Mà \(\widehat{ACD}=\widehat{ABD}\) (ABCD nội tiếp)
\(\Rightarrow\widehat{AMN}=\widehat{ABD}\) (đpcm)
Đúng 1
Bình luận (0)
Cho đường tròn (O: R) có hai đường kính AB và CD vuông góc với nhau. Lấy điểm K thuộc cung nhỏ AC, kẻ KH vuông góc AB tại H. Tia AC cắt HK tại I, tia BC cắt HK tại E, nối AE cắt đường tròn (O; R) tại F.
1. Chứng minh tứ giác BHFE là tứ giác nội tiếp.
2. Chứng minh: EF EA EC EB . . .
3. Tính theo R diện tích FEC khi H là trung điểm của OA.
4. Cho K di chuyển trên cung nhỏ AC. Chứng minh đường thẳng FH luôn đi qua một điểm cố định.
giúp mình ý 3 với ạ
Đọc tiếp
Cho đường tròn (O: R) có hai đường kính AB và CD vuông góc với nhau. Lấy điểm K thuộc cung nhỏ AC, kẻ KH vuông góc AB tại H. Tia AC cắt HK tại I, tia BC cắt HK tại E, nối AE cắt đường tròn (O; R) tại F.
1. Chứng minh tứ giác BHFE là tứ giác nội tiếp.
2. Chứng minh: EF EA EC EB . . .
3. Tính theo R diện tích FEC khi H là trung điểm của OA.
4. Cho K di chuyển trên cung nhỏ AC. Chứng minh đường thẳng FH luôn đi qua một điểm cố định.
giúp mình ý 3 với ạ
Cho tam giác ABC nhọn (AB < AC) nội tiếp đường tròn (O), các đường cao AD, BE và CF cắt nhau tại H.
a) Chứng minh tứ giác BDHF và BCEF nội tiếp.
b) Chứng minh FC là tia phân giác của \(\widehat{EFD}\).
c) Hai đường thẳng EF và BC cắt nhau tại M. Đường thẳng qua B và song song với AC cắt AM tại I và cắt AH tại K. Chứng minh tam giác HIK là tam giác cân.
Cho tứ giác ABCD nội tiếp đường tròn tâm O (AB>CD). GỌi giao điểm của AC và BD là I. Đường tròn ngoại tiếp tam giác ADI cắt AB và CD lần lượt tại E và F, EF cắt AC và BD tại M, N.
a, Chứng minh IE = IF
b, Chứng minh EF//BC và tứ giác AMND nội tiếp
c, Gọi K là tâm đường tròn ngoại tiếp tam giác ADI.
Chứng minh rằng KI vuông góc với BC
(Mình cần làm giúp phần (c) thôi ạ, cảm ơn)
Cho tam giác $ABC$ không có góc tù $(AB AC)$, nội tiếp đường tròn $(O; R)$, ($B$, $C$ cố định, $A$ di động trên cung lớn BC). Các tiếp tuyến tại $B$ và $C$ cắt nhau tại $M$. Từ $M$ kẻ đường thẳng song song với $AB$, đường thẳng này cắt $(O)$ tại $D$ và $E$ ($D$ thuộc cung nhỏ $BC$), cắt $BC$ tại $F$, cắt $AC$ tại $I$. Chứng minh rằng widehat{MBC}widehat{BAC} . Từ đó suy ra $MBIC$ là tứ giác nội tiếp.
Đọc tiếp
Cho tam giác $ABC$ không có góc tù $(AB < AC)$, nội tiếp đường tròn $(O; R)$, ($B$, $C$ cố định, $A$ di động trên cung lớn BC). Các tiếp tuyến tại $B$ và $C$ cắt nhau tại $M$. Từ $M$ kẻ đường thẳng song song với $AB$, đường thẳng này cắt $(O)$ tại $D$ và $E$ ($D$ thuộc cung nhỏ $BC$), cắt $BC$ tại $F$, cắt $AC$ tại $I$. Chứng minh rằng \(\widehat{MBC}=\widehat{BAC}\) . Từ đó suy ra $MBIC$ là tứ giác nội tiếp.
Cho tam giác không có góc tù , nội tiếp đường tròn , (, cố định, di động trên cung lớn BC). Các tiếp tuyến tại và cắt nhau tại . Từ kẻ đường thẳng song song với , đường thẳng này cắt tại và ( thuộc cung nhỏ ), cắt tại , cắt tại . Chứng minh rằng . Từ đó suy ra là tứ giác nội tiếp.
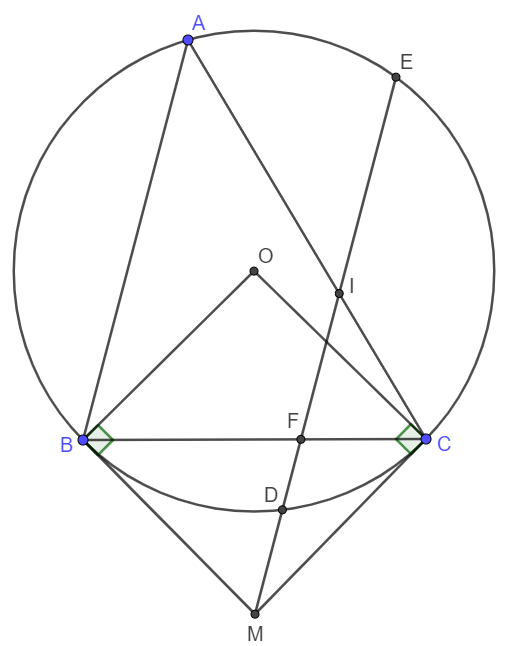
theo gt, ta co:
goc MBC= BAC (cung chan cung BC)
mat khac, ta lai co goc BAC = MIC ( dong vi)
=> goc MBC= MIC
=> tu giac BICM noi tiep
cho tứ giác ABCD nội tiếp đường tròn tâm (O) đường kính AB. Hai đường chéo AC và BD cắt nhau tại I. Kẻ IE vuông góc với AB. Chứng minh rằng:
a) Tứ giác AIDE nội tiếp một đường tròn.
b) Tia BD là tia phân giác của góc CDE.
c) Trường hợp AB không song song với CD. Chứng minh 4 điểm O, E, D, C cùng thuộc một đường tròn.
Cô hướng dẫn nhé. :)
Tứ giác AIDE nội tiếp đường tròn đường kính AI.
b. Do câu a ta có AIDE là tứ giác nội tiếp nên gó IDE = góc IAE. Lại có góc IAE = góc CDB. Từ đó suy ra DB là tia phân giac góc CDE.
c. Ta thấy góc CDE = 2 góc CAB (Chứng minh b). Lại có góc COB = 2 góc CAB. Từ đó suy ra góc CDE = góc COB. Hay OEDC là tứ giác nội tiếp ( Góc ngoài ở đỉnh bằng góc đối diện )
Chúc em học tốt ^^
Đúng 1
Bình luận (0)
Cho tứ giác ABCD nội tiếp đường tròn (O) đường kính AB. Hai đường chéo AC và BD cắt nhau tại I. Kẻ IE vuông góc với AB. Chứng minh :
a. Tứ giác ADIE nội tiếp đường tròn ;
b. Tia DB là phân giác của góc CDE ;
c. Nếu AB không song song CD, chứng minh bốn điểm O, E, D, C cùng thuộc một đường tròn.
Cho đường tròn tâm O có hai đường kính là AB và CD vuông góc với nhau tại O. Trên cung nhỏ BC lấy điểm M, AM cắt CD tại I. Tiếp tuyến của O tại M cắt tia AB tại N. Chứng minh rằng: AC là tiếp tuyến của đường tròn ngoại tiếp tam giác CMI.

















