Cho hình thang ABCD(AB//CD), AB<CD. CMR: \(\widehat{A}+\widehat{B}>\widehat{C}+\widehat{D}\)

Những câu hỏi liên quan
Cho hình thang ABCD (AB // CD) có \(\widehat{A}=3\widehat{D}\), \(\widehat{B}=\widehat{C}\) , AB = 3cm, CD = 4cm. Tính độ dài đường cao AH của hình thang và tính diện tích hình thang.
Vì AB // CD nên \(\widehat{B}+\widehat{C}=180^o\)
Mà \(\widehat{B}=\widehat{C}\)
\(\Rightarrow\widehat{B}=\widehat{C}=\frac{180^o}{2}=90^o\)
\(\Rightarrow\)Tứ giác ABCH có 3 góc vuông là hình chữ nhật
Ta có : \(DH=DC-HC\)
\(=DC-AB\) (Vì AB = HC)
\(=4-3\)
\(=1\left(cm\right)\)
Lại có : \(\hept{\begin{cases}\widehat{A}=3\widehat{D}\\\widehat{A}+\widehat{D}=180^o\left(slt\right)\end{cases}\Rightarrow}\hept{\begin{cases}\widehat{A}=135^o\\\widehat{D}=45^o\end{cases}}\)
\(\Rightarrow\)△AHD vuông tại H có ^ADH = 45o
\(\Rightarrow\)△AHD vuông cân tại H
\(\Rightarrow\)AH = DH
\(\Rightarrow\)AH = 1 (cm)
Vậy \(S_{ABCD}=\frac{\left(AB+CD\right)\cdot AH}{2}=\frac{\left(4+3\right)\cdot1}{2}=3,5\left(cm^2\right)\)
Xét hình thang ABCD có \(AB//CD\)(gt) có:
\(\widehat{A}+\widehat{D}=180^0\)(trong cùng phía)
Mà \(\widehat{A}=3\widehat{D}\left(gt\right)\)
\(\Rightarrow3\widehat{D}+\widehat{D}=180^0\)
\(\Leftrightarrow4\widehat{D}=180^0\)
\(\Leftrightarrow\widehat{D}=45^0\)
\(\Rightarrow\widehat{A}=3.45^0=135^0\)
Ta có:\(AB//CD\left(gt\right)\)\(\Rightarrow\widehat{B}+\widehat{C}=180^0\)
Mà \(\widehat{B}=\widehat{C}\left(gt\right)\)\(\Rightarrow\widehat{B}+\widehat{B}=180^0\)
\(\Leftrightarrow2\widehat{B}=180^0\)
\(\Leftrightarrow\widehat{B}=90^0\Rightarrow\widehat{C}=90^0\)
Xét tứ giác ABCH có \(\widehat{B}=\widehat{C}=\widehat{H}=90^0\left(cmt\right)\)
\(\Rightarrow\)Tứ giác ABCH là hình chữ nhật (DHNB)
\(\Rightarrow AB=CH=3cm\)(t/c) \(\Rightarrow DH=CD-CH=4-3=1\left(cm\right)\)
Xét \(\Delta AHD\)có \(\widehat{H}=90^0,\widehat{D}=45^0\left(cmt\right)\)
\(\Rightarrow\Delta AHD\)vuông cân tại A (DHNB) \(\Rightarrow AH=DH=1cm\)(t/c)
Diện tích hình thang ABCD có:
\(S_{ABCD}=\frac{\left(AB+CD\right)\times AH}{2}=\frac{\left(3+4\right)\times1}{2}=3,5\left(cm^2\right)\)
Đáp số \(3,5cm^2\)
Học tốt
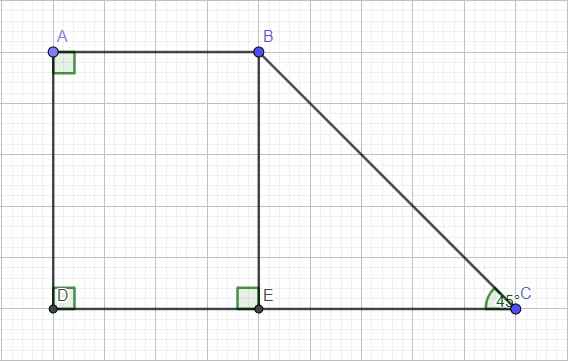
Cho hình thang \(ABCD\) có \(\widehat{A}\)=\(\widehat{D}\)=90o, \(\widehat{C}\)= 45o. Biết đường cao của hình thang bằng 4cm, \(AB+CD=10cm\). Tính 2 đáy.
Kẻ đường cao BE ứng với CD \(\Rightarrow BE=4\left(cm\right)\)
Trong tam giác vuông BCE ta có:
\(\widehat{EBC}=90^0-\widehat{C}=90^0-45^0=45^0\)
\(\Rightarrow\widehat{EBC}=\widehat{C}\Rightarrow\Delta BCE\) vuông cân tại E
\(\Rightarrow EC=BE=4\left(cm\right)\)
Tứ giác ABED là hình chữ nhật (tứ giác có 3 góc vuông)
\(\Rightarrow AB=DE\)
Ta có:
\(AB+CD=10\left(cm\right)\)
\(\Leftrightarrow AB+DE+EC=10\)
\(\Leftrightarrow2AB+4=10\)
\(\Rightarrow AB=3\left(cm\right)\)
\(\Rightarrow DE=AB=3cm\Rightarrow CD=DE+EC=7\left(cm\right)\)
Đúng 1
Bình luận (0)
Cho hình thang ABCD (AB song song với CD) có \(\widehat{A}=3.\widehat{D}\), \(\widehat{B}=\widehat{C}\), AB =3cm, CD=4cm. tính đường cao AH của hình thang và diện tích của hình thang.
Xem thêm câu trả lời
Cho hình thang cân ABCD có AB//CD, \(\widehat{C}\) = 60o. DB là tia phân giác của \(\widehat{D}\). Tính các cạnh của hình thang biết chu vi hình thang bằng 20cm, CD = 8cm.
Hình thang ABCD có AB//CD, \(\widehat{D}=60^o,\widehat{C}=30^o,AB=2cm,CD=6cm\). Tính đường cao của hình thang
Hình thang ABCD (AB //CD) có \(\widehat{A}-\widehat{D}=40^0;\widehat{A}=2\widehat{C}\). Tính các góc của hình thang ?
Ta có hình vẽ:
Vì AB//CD
nên góc A+ góc D = 180 độ (1)
góc A - góc D = 20 độ
=> góc A = 20 độ + góc D (2)
thay (1) vào (2) ta được: 20 độ + góc D + góc D = 180 độ
20 độ + 2 lần góc D = 180 độ
2 lần góc D = 180- 20 = 160 độ
góc D = 160/2 = 80 độ
=> góc A = góc D + 20 độ = 80+ 20= 100 độ
mà góc B = 2 lần góc C
góc B + góc C = 180 độ (trong cùng phía)
hay 2 lần góc C + góc C = 180 độ
3 lần góc C = 180 độ
góc C = 180/ 3= 60 độ
=> góc B = góc C . 2 = 60. 2= 120 độ
Vậy góc A= 100 độ
góc B = 120 độ
góc C = 60 độ
góc D = 80 độ
Đúng 0
Bình luận (0)
Hình thang ABCD (AB // CD) có \(\widehat{A}-\widehat{D}=20^0,\widehat{B}=2\widehat{C}\). Tính các góc của hình thang ?
Bài giải:
Ta có 200; 1800
Từ 200
=> = 200 +
Nên 200 + +=200 +2 =1800
=> 2=1600 => = 800
Thay = 800 vào = 200 + ta được =200 + 800 = 1000
Lại có ; 1800
nên
Đúng 0
Bình luận (0)

Ta có :AB//CD\(\Rightarrow\widehat{A}+\widehat{D}=180^o\) (do 2 góc ở vị trí trong cùng phía )
Từ \(\widehat{A}-\widehat{D}=20^o\Rightarrow\widehat{A}=20^o+\widehat{D}\) \(^{\left(1\right)}\)
Nên \(\widehat{A}+\widehat{D}=20^o+\widehat{D}+\widehat{D}=20^o+2.\widehat{D}=180^o\)
\(\Rightarrow2\widehat{D}=160^o\Rightarrow\widehat{D}=80^o\)
Thay \(\widehat{D}=80^o\) vào \(^{\left(1\right)}\) , ta được:
\(\widehat{A}=20^o+80^o=100^o\)
Lại có:\(\widehat{B}+\widehat{C}=180^o\) (do 2 góc ở vị trí trong cùng phía )
và \(\widehat{B}=2.\widehat{C}\)
nên \(2.\widehat{C}+\widehat{C}=180^o\) hay \(3.\widehat{C}=180^o\Rightarrow\widehat{C}=60^o\)
Do đó: \(\widehat{B}=2.\widehat{C}=2.60^o=120^o\)
Vậy \(\widehat{A}=100^o;\widehat{B}=120^o;\widehat{C}=60^o;\widehat{D}=80^o\)
Đúng 0
Bình luận (0)
Ta có :AB//CD⇒ˆA+ˆD=180o⇒A^+D^=180o (do 2 góc ở vị trí trong cùng phía )
Từ ˆA−ˆD=20o⇒ˆA=20o+ˆDA^−D^=20o⇒A^=20o+D^ (1)(1)
Nên ˆA+ˆD=20o+ˆD+ˆD=20o+2.ˆD=180oA^+D^=20o+D^+D^=20o+2.D^=180o
⇒2ˆD=160o⇒ˆD=80o⇒2D^=160o⇒D^=80o
Thay ˆD=80oD^=80o vào (1)(1) , ta được:
ˆA=20o+80o=100oA^=20o+80o=100o
Lại có:ˆB+ˆC=180oB^+C^=180o (do 2 góc ở vị trí trong cùng phía )
và ˆB=2.ˆCB^=2.C^
nên 2.ˆC+ˆC=180o2.C^+C^=180o hay 3.ˆC=180o⇒ˆC=60o3.C^=180o⇒C^=60o
Do đó: ˆB=2.ˆC=2.60o=120oB^=2.C^=2.60o=120o
Vậy ˆA=100o;ˆB=120o;ˆC=60o;ˆD=80o
Đúng 0
Bình luận (0)
Cho hình thang vuông ABCD (AB // CD) có \(\widehat{A}=\widehat{D}=90^0,\widehat{B}=60^0,CD=30cm,CA\perp CB\) . Tính diện tích của hình thang ABCD.
Cho hình thang ABCD (AB // CD) có \(\widehat{B}-\widehat{C}=60\) độ và \(\widehat{D}=\dfrac{4}{5}\widehat{A}\).
Tính số đo các góc của hình thang ABCD