a) Ta có 25²=15²+20² hay BC²=AB²+AC²

=> ▲ABC vuông tại A

b) Xét ▲ABC vuông tại A có
SinB = \(\frac{AC}{BC}=\frac{20}{25}=\frac{4}{5}\)
TanC = \(\frac{AB}{AC}=\frac{15}{20}=\frac{3}{4}\)
=> SinB + TanC = \(\frac{4}{5}+\frac{3}{4}=\frac{31}{20}\)

c) I là trung điểm AC => AI = 10cm.
=> BI² = 10²+15²= 325 => BI = \(5\sqrt{13}\)
Xét ▲ABI có TanI = \(\frac{3}{2}\)=> góc BIA = 56'18'

=> BIC = 180 - 56'18' = 123 độ 41 phút.

\(a,AB^2+AC^2=15^2+20^2=625=25^2=BC^2\)

Vậy ABC là tam giác vuông tại A (pytago đảo)

\(b,\)Áp dụng HTL tam giác ABC vuông tại A, đường cao AH

\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\\AH^2=BH\cdot HC\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}BH=\dfrac{AB^2}{BC}=9\left(cm\right)\\CH=\dfrac{AC^2}{BC}=12\left(cm\right)\\AH=\sqrt{9\cdot12}=6\sqrt{3}\left(cm\right)\end{matrix}\right.\)

Vì AM là phân giác nên \(\dfrac{MB}{MC}=\dfrac{AB}{AC}=\dfrac{3}{4}\Rightarrow MB=\dfrac{3}{4}MC\)

Mà \(MB+MC=BC=25\Rightarrow\dfrac{7}{4}MC=25\)

\(\Rightarrow MC=\dfrac{100}{7}\left(cm\right);MB=\dfrac{75}{7}\left(cm\right)\)

a: Xét ΔBAI vuông tại A và ΔBAC vuông tại A có

BA chung

AI=AC

=>ΔBAI=ΔBAC

b: Xét ΔEIA và ΔFCA có

EI=FC

góc I=góc C

IA=CA

=>ΔEIA=ΔFCA

=>AE=AF

=>ΔAEF cân tại A

a, Vì AB²+AC²=15²+20²=625 cm

         BC²=25²=625 cm

=> AB²+AC²=BC² => tg ABC vuông tại A

b, Ta có AB²+AC²=32 cm

              BC²=32 cm

=> AB²+AC²=BC² => tg ABC vuông tại A

Mà AB=AC=4cm

=> tg ABC vuông cân tại A

a: BC=căn 15^2+20^2=25cm

AH=15*20/25=12cm

HC=AC^2/BC=20^2/25=16cm

Xét ΔACB vuông tại A có sin ACB=AB/BC=3/5

=>góc ACB=37 độ

b: Xét ΔHAB có HI/HA=HK/HB

nên IK//AB

=>KI vuông góc AC

Xét ΔCAK có

KI,AH là đường cao

KI cắt AH tại I

=>I là trực tâm

c: Xét ΔKBA và ΔIAC có

góc KBA=góc IAC

AB/AC=KB/IA=HB/HA

=>ΔKBA đồng dạng với ΔIAC

a) Ta có: \(BD + DC = BC \Rightarrow DC = BC - BD = 25 - BD\)

Vì \(AD\) là phân giác của góc \(BAC\) nên theo tính chất đường phân giác ta có:

\(\frac{{BD}}{{DC}} = \frac{{AB}}{{AC}} \Leftrightarrow \frac{{BD}}{{25 - BD}} = \frac{{15}}{{20}} \Leftrightarrow 20.BD = 15.\left( {25 - BD} \right) \Rightarrow 20.BD = 375 - 15.BD\)

\( \Leftrightarrow 20BD + 15BD = 375 \Leftrightarrow 35BD = 375 \Rightarrow BD = \frac{{375}}{{35}} = \frac{{75}}{7}\)

\( \Rightarrow DC = 25 - \frac{{75}}{7} = \frac{{100}}{7}\)

Vậy \(BD = \frac{{75}}{7}cm;DC = \frac{{100}}{7}cm\).

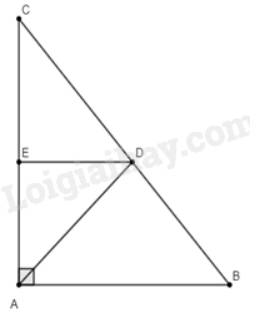
 Vì \(DE//AB\) nên \(\frac{{DC}}{{BC}} = \frac{{DE}}{{AB}} \Rightarrow \frac{{\frac{{100}}{7}}}{{25}} = \frac{{DE}}{{15}} \Leftrightarrow DE = \frac{{100}}{7}.15:25 = \frac{{60}}{7}\) (hệ quả của định lí Thales).

Vậy \(BD = \frac{{75}}{7}cm;DC = \frac{{100}}{7}cm;DE = \frac{{60}}{7}cm\).

b) Xét tam giác \(ABC\) có:

\(B{C^2} = {25^2} = 625;A{C^2} = {20^2} = 400;A{B^2} = {15^2} = 225\)

\( \Rightarrow B{C^2} = A{C^2} + A{B^2}\)

Do đó, tam giác\(ABC\) là tam giác vuông tại \(A\).

c) Diện tích tam giác \(ABC\) là

\({S_{ABC}} = \frac{1}{2}AB.AC = \frac{1}{2}.15.20 = 150\left( {c{m^2}} \right)\).

Xét tam giác \(ADB\) và tam giác \(ABC\) ta có:

\(\frac{{BD}}{{BC}} = \frac{{\frac{{75}}{7}}}{{25}} = \frac{3}{7}\) và có chung chiều cao hạ từ đỉnh \(A\). Do đó, diện tích tam giác \(ADB\) bằng \(\frac{3}{7}\) diện tích tam giác \(ABC\).

Diện tích tam giác \(ADB\) là:

\({S_{ADB}} = 150.\frac{3}{7} = \frac{{450}}{7}\left( {c{m^2}} \right)\).

Diện tích tam giác \(ACD\) là:

\({S_{ACD}} = {S_{ABC}} - {S_{ADB}} = 150 - \frac{{450}}{7} = \frac{{600}}{7}\)

Vì \(ED//AB \Rightarrow \frac{{CE}}{{AE}} = \frac{{CD}}{{BD}} = \frac{{\frac{{100}}{7}}}{{\frac{{75}}{{100}}}} = \frac{4}{3}\)

Xét tam giác \(ADE\) và tam giác \(DCE\) ta có:

\(\frac{{CE}}{{AE}} = \frac{4}{3}\) và hai tam giác này có chung đường cao hạ từ \(D\).

Do đó, \(\frac{{{S_{ADE}}}}{{{S_{DCE}}}} = \frac{4}{3}\).

Diện tích tam giác \(ADE\) là

\({S_{ADE}} = \frac{{600}}{7}:\left( {3 + 4} \right).4 = \frac{{2400}}{{49}}\left( {c{m^2}} \right)\)

\({S_{DCE}} = \frac{{600}}{7}:\left( {3 + 4} \right).3 = \frac{{1800}}{{49}}\left( {c{m^2}} \right)\).

a: Xét ΔABC có AD là phân giác

nên DB/AB=DC/AC

=>DB/3=DC/4=(DB+DC)/(3+4)=25/7

=>DB=75/7cm; DC=100/7cm

Xét ΔABC có DE//AB

nên DE/AB=CD/CB

=>DE/15=100/7:25=4/7

=>DE=60/7cm

b: Xét ΔABC có BC^2=AB^2+AC^2

nen ΔABC vuông tại A

=>S ABC=1/2*15*20=10*15=150cm²

c: DB/DC=3/7

=>S ABD/S ACB=3/7

=>S ABD=150*3/7=450/7cm²

a) Ta có: AB² + AC² = 20² + 15² = 625

BC² = 25² = 625

nên AB² + AC² = BC²

    Suy ra tam giác ABC vuông do định lí Pi-ta-go đảo

b)    Áp dụng định lí Pitago trong tam giác vuông ACH được:

    HC² + HA² = AC²

CH² = 15² - 12²

CH² = 81

=> CH=9 (cm)

     Áp dụng định lí Pitago trong tam giác vuông AHB được:

                 AH² + BH² = AB²

               12² + BH² = 20²

=> BH² = 20² - 12² = 256

=> BH=16 cm 

Hình bạn tự kẻ nhé . 

a)  Ta có AB²+AC² = 20²+15²= 625

Lại có BC² = 25² = 625

=> Tam giác ABC vuông ( Py ta go )

b) Ta có AH là đường cao 

=> Tam giác ABH và tam giác ACH vuông tại H

Áp dụng Py ta go vào tam giác vuông ACH ta được :

AC²=CH²+ AH²

=> 15² = CH² + 12²

=> CH² =  15² - 12² = 81

=> CH = 9 ( cm)

=> BH = BC-CH = 25- 9 = 16  ( cm)