Rút gọn hằng đẳng thức
(x+y)mũ 3
Những câu hỏi liên quan
18 tháng 11 2023 lúc 20:50
RÚT GỌN CÁC BIỂU THỨC SAU:
Gợi ý: Dùng hằng đẳng thức để rút gọn nhanh hơn (nhưng cũng phải biến đổi rõ ràng ra rồi mới ra hằng đẳng thức chứ ko đc làm nhanh bằng cách ghi hằng đẳng thức ngay!)
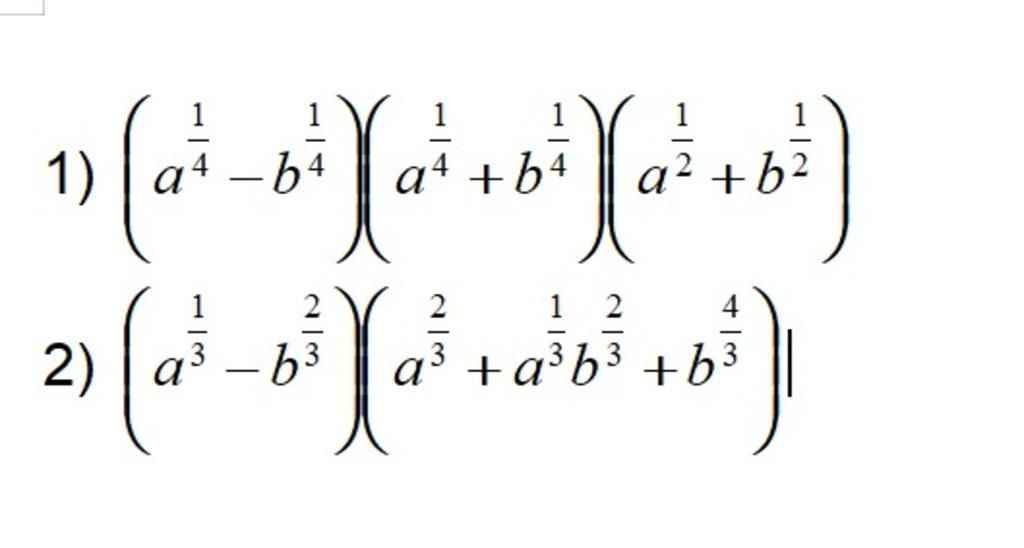
`1)(a^[1/4]-b^[1/4])(a^[1/4]+b^[1/4])(a^[1/2]+b^[1/2])`
`=[(a^[1/4])^2-(b^[1/4])^2](a^[1/2]+b^[1/2])`
`=(a^[1/2]-b^[1/2])(a^[1/2]+b^[1/2])`
`=a-b`
`2)(a^[1/3]-b^[2/3])(a^[2/3]+a^[1/3]b^[2/3]+b^[4/3])`
`=(a^[1/3]-b^[2/3])[(a^[1/3])^2+a^[1/3]b^[2/3]+(b^[2/3])^2]`
`=(a^[1/3])^3-(b^[2/3])^3`
`=a-b^2`
Đúng 4
Bình luận (0)
Rút gọn biểu thức sau 4x2 - ( x + 3 ) . ( x - 3 ) + x bằng phương pháp dùng hằng đẳng thức
\(4x^2-\left(x+3\right).\left(x-3\right)+x\)\(=4x^2-\left(x^2-3^2\right)+x\)
\(=4x^2-\left(x^2-9\right)+x\)
\(=4x^2-x^2+9+x\)
\(=3x^2+x+9\)
Khai triển và rút gọn hằng đẳng thức
(x-3)(x-5)-(2x+3)2
C=\(\left(x+2y\right)^3\)-6\(\left(x+2y\right)^2\)+12\(\left(x+2y\right)\)-8 tại x=20, y=1
Áp dụng hằng đẳng thức để rút gọn rồi mới thay số ạ
`C=(x+2y)^3-6(x+2y)^2+12(x+2y)-8`
`C=(x+2y-2)^3` (HĐT số `5`)
Thay `x=20;y=1` vào `C` có:
`C=(20+2.1-2)^3=8000`.
Đúng 2
Bình luận (0)
Rút gọn biểu thức sau bằng cách áp dụng hằng đẳng thức đáng nhớ:
(x^2+1/x+1/9)(x-1/3)-(x-1/3)^3
rút gọn giúp mình hằng đẳng thức câu này c) (x – 5).(x + 5) – (x + 5)
c: Ta có: \(\left(x-5\right)\left(x+5\right)-\left(x+5\right)\)
\(=x^2-25-x-5\)
\(=x^2-x-30\)
Đúng 0
Bình luận (0)
Bài 3: Rút gọn biểu thức (Dùng hằng đẳng thức)1, (x+y)^2-(x-y)^22, (x+y)^3-(x-y)^3-2y^33,(x+y)^2-2(x+y)(x-y)+(x-y)^24,(2x+3)^2-2(2x+3)(2x+5)+(2x+5)^25, 9^8. 2^8-(18^4+1)(18^4-1)
Đọc tiếp
Bài 3: Rút gọn biểu thức (Dùng hằng đẳng thức)
1, (x+y)\(^2\)-(x-y)\(^2\)
2, (x+y)\(^3\)-(x-y)\(^3\)-2y\(^3\)
3,(x+y)\(^2\)-2(x+y)(x-y)+(x-y)\(^2\)
4,(2x+3)\(^2\)-2(2x+3)(2x+5)+(2x+5)\(^2\)
5, 9\(^8\). 2\(^8\)-(18\(^4\)+1)(18\(^4\)-1)
\(1,\left(x+y\right)^2-\left(x-y\right)^2=\left[\left(x+y\right)-\left(x-y\right)\right]\left[\left(x+y\right)+\left(x-y\right)\right]=\left(x+y-x+y\right)\left(x+y+x-y\right)=2y.2x=4xy\)
\(2,\left(x+y\right)^3-\left(x-y\right)^3-2y^3\)
\(=x^3+3x^2y+3xy^2+y^3-x^3+3x^2y-3xy^2+y^3-2y^3\)
\(=6x^2y\)
\(3,\left(x+y\right)^2-2\left(x+y\right)\left(x-y\right)+\left(x-y\right)^2\\ =\left[\left(x+y\right)-\left(x-y\right)\right]^2\\ =\left(x+y-x+y\right)^2\\ =4y^2\)
\(4,\left(2x+3\right)^2-2\left(2x+3\right)\left(2x+5\right)+\left(2x+5\right)^2\\ =\left[\left(2x+3\right)-\left(2x+5\right)\right]^2\\ =\left(2x+3-2x-5\right)^2\\ =\left(-2\right)^2\\ =4\)
\(5,9^8.2^8-\left(18^4+1\right)\left(18^4-1\right)\\ =18^8-\left[\left(18^4\right)^2-1\right]\\ =18^8-18^8+1\\ =1\)
Đúng 2
Bình luận (0)
1: =x^2+2xy+y^2-x^2+2xy-y^2=4xy
2: =x^3+3x^2y+3xy^2+y^3-x^3+3x^2y-3xy^2+y^3-2y^3
=6x^2y
3: =(x+y-x+y)^2=(2y)^2=4y^2
4: =(2x+3-2x-5)^2=(-2)^2=4
5: =18^8-18^8+1=1
Đúng 0
Bình luận (0)
bài 3 ; áp dụng hằng đẳng thức để thực hiện phép chia
h, ( 27x mũ 3 - 8 ) : ( 3x - 2 )
f, ( x mũ 2 - 2xy mũ 2 + y mũ 2 ) : ( x - y mũ 2 )
g, ( x mũ 4 - 2x mũ 2 + 1 ) : ( 1 - x mũ 2 )
h, \(27x^3-8=\left(3x-2\right)\left(9x^2+6x+4\right)\)
\(\Rightarrow\left(27x^3-8\right):\left(3x-2\right)\\ =\left(3x-2\right)\left(9x^2+6x+4\right):\left(3x-2\right)\\ =9x^2+6x+4\)
g, \(x^4-2x^2+1=\left(x^2-1\right)^2\)
\(\Rightarrow\left(x^4-2x^2+1\right):\left(1-x^2\right)\\ =\left(x^2-1\right)^2:\left(1-x^2\right)\\ =x^2-1\)
Đúng 0
Bình luận (0)
Câu 1: (3đ) Áp dụng hằng đẳng thức tính:
a. A = 2xy mũ 2+x mũ 2 y mũ 4 +1 tại x=2y=16
b. B = x mũ 3 +9x+27x+27 tại x=97
c. (2x+y mũ 2-1)(2x+y mũ 2+1)