cho hình bình hành ABCD, gọi I là trung điểm của BC, G là trọng tâm tam giác CDI, Biểu diễn vecto AG qua 2 vecto AB và AD

Những câu hỏi liên quan
Cho ABCD là hình bình hành. Đặt \(\overrightarrow {AB} = \overrightarrow a ,\overrightarrow {AD} = \overrightarrow b .\) Gọi G là trọng tâm của tam giác ABC. Biểu thị các vecto \(\overrightarrow {AG} ,\overrightarrow {CG} \) theo hai vecto \(\overrightarrow a ,\overrightarrow b .\)
Cách 1:
Gọi O là giao điểm của AC và BD.

Ta có:
\(\begin{array}{l}\overrightarrow {AG} = \overrightarrow {AB} + \overrightarrow {BG} = \overrightarrow a + \overrightarrow {BG} ;\\\overrightarrow {CG} = \overrightarrow {CB} + \overrightarrow {BG} = \overrightarrow {DA} + \overrightarrow {BG} = - \overrightarrow b + \overrightarrow {BG} ;\end{array}\)(*)
Lại có: \(\overrightarrow {BD} =\overrightarrow {BA} + \overrightarrow {AD} = - \overrightarrow a + \overrightarrow b \).
\(\overrightarrow {BG} ,\overrightarrow {BD} \) cùng phương và \(\left| {\overrightarrow {BG} } \right| = \frac{2}{3}BO = \frac{1}{3}\left| {\overrightarrow {BD} } \right|\)
\( \Rightarrow \overrightarrow {BG} = \frac{1}{3}\overrightarrow {BD} = \frac{1}{3}\left( { - \overrightarrow a + \overrightarrow b } \right)\)
Do đó (*) \( \Leftrightarrow \left\{ \begin{array}{l}\overrightarrow {AG} = \overrightarrow a + \overrightarrow {BG} = \overrightarrow a + \frac{1}{3}\left( { - \overrightarrow a + \overrightarrow b } \right) = \frac{2}{3}\overrightarrow a + \frac{1}{3}\overrightarrow b ;\\\overrightarrow {CG} = -\overrightarrow b + \overrightarrow {BG} = -\overrightarrow b + \frac{1}{3}\left( { - \overrightarrow a + \overrightarrow b } \right) = - \frac{1}{3}\overrightarrow a - \frac{2}{3}\overrightarrow b ;\end{array} \right.\)
Vậy \(\overrightarrow {AG} = \frac{2}{3}\overrightarrow a + \frac{1}{3}\overrightarrow b ;\;\overrightarrow {CG} = - \frac{1}{3}\overrightarrow a - \frac{2}{3}\overrightarrow b .\)
Đúng 1
Bình luận (0)
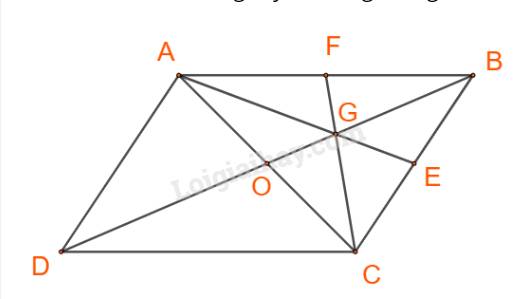
Cách 2:
Gọi AE, CF là các trung tuyến trong tam giác ABC.
Ta có:
\(\overrightarrow {AG} = \frac{2}{3}\overrightarrow {AE} = \frac{2}{3}.\frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right) = \frac{2}{3}.\frac{1}{2}\left[ {\overrightarrow {AB} + \left( {\overrightarrow {AB} + \overrightarrow {AD} } \right)} \right] \\= \frac{1}{3}\left( {2\overrightarrow a + \overrightarrow b } \right) = \frac{2}{3}\overrightarrow a + \frac{1}{3}\overrightarrow b \)
\(\overrightarrow {CG} = \frac{2}{3}\overrightarrow {CF} = \frac{2}{3}.\frac{1}{2}\left( {\overrightarrow {CA} + \overrightarrow {CB} } \right) = \frac{2}{3}.\frac{1}{2}\left[ {\left( {\overrightarrow {CB} + \overrightarrow {CD} } \right) + \overrightarrow {CB} } \right] = \frac{1}{3}\left( {2\overrightarrow {CB} + \overrightarrow {CD} } \right) = \frac{1}{3}\left( { - 2\overrightarrow {AD} - \overrightarrow {AB} } \right) = - \frac{1}{3}\overrightarrow a - \frac{2}{3}\overrightarrow b \)
Vậy \(\overrightarrow {AG} = \frac{2}{3}\overrightarrow a + \frac{1}{3}\overrightarrow b ;\;\overrightarrow {CG} = - \frac{1}{3}\overrightarrow a - \frac{2}{3}\overrightarrow b .\)
Đúng 0
Bình luận (0)
cho hình bình hành ABCD gọi I là trung điểm của CD . G là trong tâm cũa tam giác BCI hãy phân tích vecto BI và AB và AD
Lời giải:
** Điểm G không có vai trò gì trong bài toán
\(\overrightarrow{BI}=\overrightarrow{BD}+\overrightarrow{DI}=(\overrightarrow{BA}+\overrightarrow{BC})+\frac{1}{2}\overrightarrow{DC}\)
\(=-\overrightarrow{AB}+\overrightarrow{AD}+\frac{1}{2}\overrightarrow{AB}=\overrightarrow{AD}-\frac{1}{2}\overrightarrow{AB}\)
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD. Gọi P, Q, R, S lần lượt là trung điểm của AB, BC, CD, DA. Các đoạn thẳng PC, QD, RA, SB cắt nhau tại các điểm tạo thành tứ giác KLMN.
1) Cmr KLMN là hình bình hành
2) Biểu diễn vecto MK, vecto NL theo vecto AB bằng vecto x, vecto AD bằng vecto y
Cho hình bình hành ABCD. Gọi E là điểm thỏa mãn 4 overrightarrow{DE} overrightarrow{DC} và G là trọng tâm tam giác ABE. Đường thẳng AG cắt BC tại F. Biểu diễn overrightarrow{AG} theo overrightarrow{AB} , overrightarrow{AD} và tính tỉ số dfrac{BF}{BC}
Đọc tiếp
Cho hình bình hành ABCD. Gọi E là điểm thỏa mãn 4 \(\overrightarrow{DE}\) = \(\overrightarrow{DC}\) và G là trọng tâm tam giác ABE. Đường thẳng AG cắt BC tại F. Biểu diễn \(\overrightarrow{AG}\) theo \(\overrightarrow{AB}\) , \(\overrightarrow{AD}\) và tính tỉ số \(\dfrac{BF}{BC}\)
Cho tam giác ABC gọi G là trọng tâm, M là trung điểm BC. PQ là đường trung bình của tam giác ABC. Lấy điểm I bấc kì nằm trên PQ.
Biểu diễn vecto IM theo 2 vecto BI và vecto IC.
Mình không vẽ hình được, có ai tốt bụng thì vẽ hộ luôn được không. Cảm ơn trước ạ!
Cho hình bình hành ABCD tâm O. Gọi trung điểm của BC, CD theo thứ tự là P, Q. Hãy biểu diễn các vecto BC, AP, AQ, PQ theo các vecto AB và AO
Cho tam giác ABC trọng tâm G . Gọi I là trung điểm của AG Chứng minh : vecto AB + vecto AC + 6vecto GI = vecto 0
Gọi M là trung điểm BC, theo tính chất trọng tâm:
\(\overrightarrow{AG}=\dfrac{2}{3}\overrightarrow{AM}\)
Mà I là trung điểm AG \(\Rightarrow\overrightarrow{IG}=\dfrac{1}{2}\overrightarrow{AG}=\dfrac{1}{3}\overrightarrow{AM}\Rightarrow\overrightarrow{GI}=-\dfrac{1}{3}\overrightarrow{AM}\)
Lại có: M là trung điểm BC \(\Rightarrow\overrightarrow{MB}+\overrightarrow{MC}=\overrightarrow{0}\)
Nên ta có:
\(\overrightarrow{AB}+\overrightarrow{AC}+6\overrightarrow{GI}=\overrightarrow{AM}+\overrightarrow{MB}+\overrightarrow{AM}+\overrightarrow{MC}+6.\left(-\dfrac{1}{3}\right)\overrightarrow{AM}\)
\(=2\overrightarrow{AM}-2\overrightarrow{AM}=\overrightarrow{0}\) (đpcm)
Đúng 1
Bình luận (0)
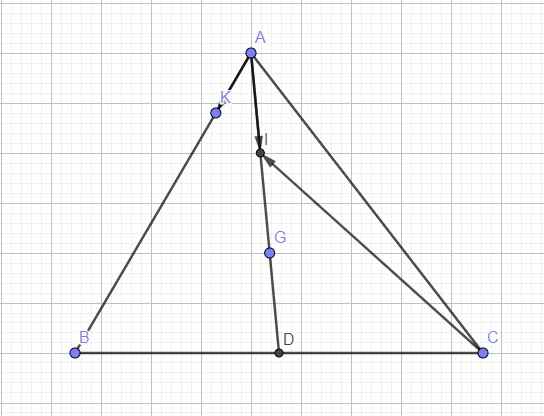
Cho tam giác ABC có trung tuyến AD, trọng tâm G, I là trung điểm AG, K thuộc đoạn AB. AK=1/5 AB, phân tích các vecto sau qua vecto CA, vecto CB a. Vecto AI b. Vecto AK c. Vecto CI d. Vecto CK
Do G là trọng tâm tam giác
\(\Rightarrow\overrightarrow{AG}=\dfrac{2}{3}\overrightarrow{AD}=\dfrac{2}{3}\left(\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}\right)=\dfrac{1}{3}\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{AC}=\dfrac{1}{3}\overrightarrow{AC}+\dfrac{1}{3}\overrightarrow{CB}+\dfrac{1}{3}\overrightarrow{AC}\)
\(=\dfrac{2}{3}\overrightarrow{AC}+\dfrac{1}{3}\overrightarrow{CB}=-\dfrac{2}{3}\overrightarrow{CA}+\dfrac{1}{3}\overrightarrow{CB}\)
Do I là trung điểm AG
\(\Rightarrow\overrightarrow{AI}=\dfrac{1}{2}\overrightarrow{AG}=\dfrac{1}{2}\left(-\dfrac{2}{3}\overrightarrow{CA}+\dfrac{1}{3}\overrightarrow{CB}\right)=-\dfrac{1}{3}\overrightarrow{CA}+\dfrac{1}{6}\overrightarrow{CB}\)
\(\overrightarrow{AK}=\dfrac{1}{5}\overrightarrow{AB}=\dfrac{1}{5}\left(\overrightarrow{AC}+\overrightarrow{CB}\right)=-\dfrac{1}{5}\overrightarrow{CA}+\dfrac{1}{5}\overrightarrow{CB}\)
\(\overrightarrow{CI}=\overrightarrow{CA}+\overrightarrow{AI}=\overrightarrow{CA}-\dfrac{1}{3}\overrightarrow{CA}+\dfrac{1}{6}\overrightarrow{CB}=\dfrac{2}{3}\overrightarrow{CA}+\dfrac{1}{6}\overrightarrow{CB}\)
\(\overrightarrow{CK}=\overrightarrow{CA}+\overrightarrow{AK}=\overrightarrow{CA}-\dfrac{1}{5}\overrightarrow{CA}+\dfrac{1}{5}\overrightarrow{CB}=\dfrac{4}{5}\overrightarrow{CA}+\dfrac{1}{5}\overrightarrow{CB}\)
Đúng 0
Bình luận (0)
| Cho tam giác ABC có trọng tâm G, gọi M, N, P lần lượt là trung điểm của BC, CA, AB |
a) Tìm các vectơ bằng vecto MN b) Dựng điểm I sao cho vecto AG bằng vecto PI
c) Tứ giác BGMI là hình gì ?