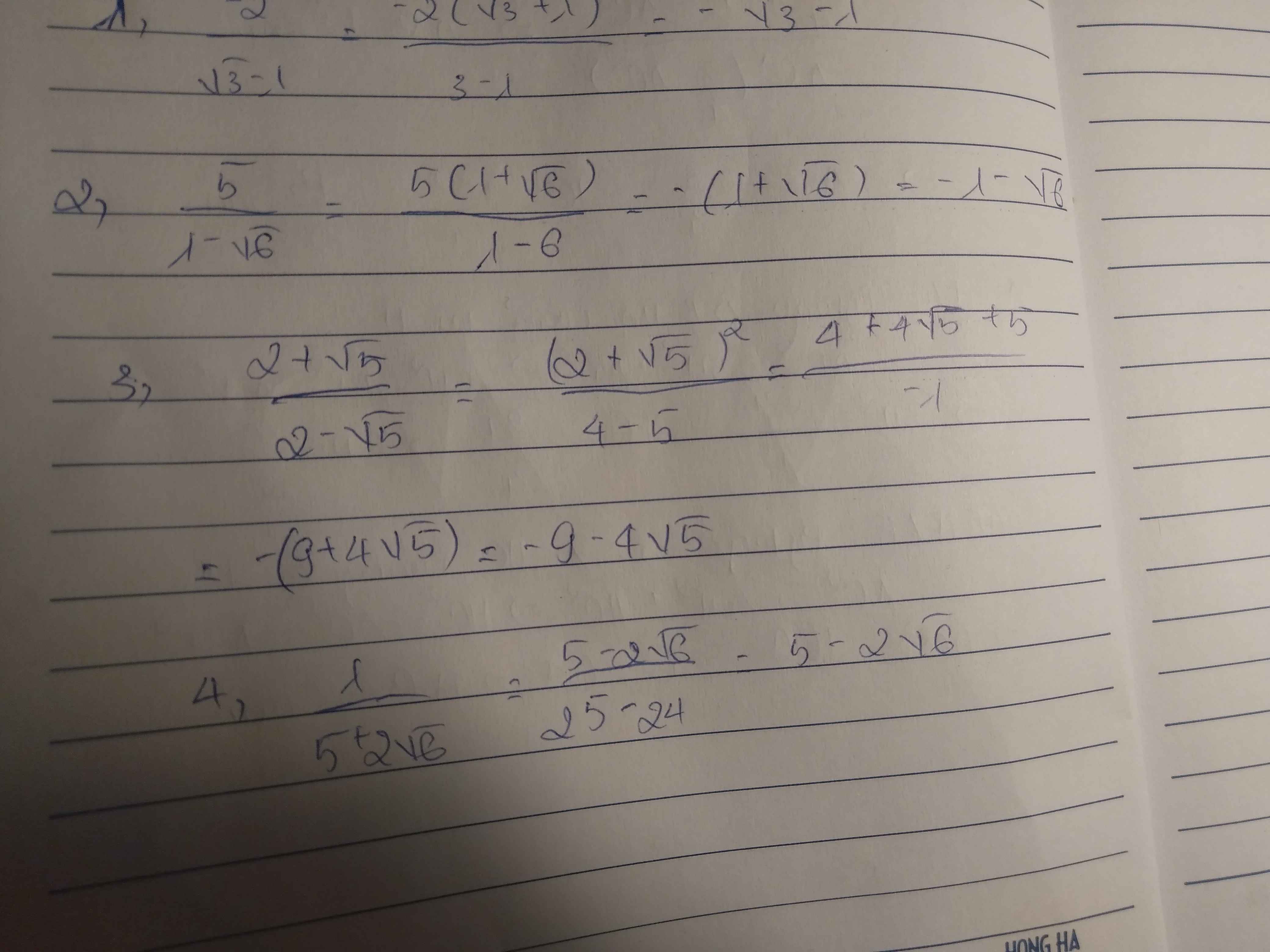\(\sqrt{6+2\sqrt{3}+2\sqrt{2}+2\sqrt{6}}-\sqrt{5-2\sqrt{6}}=1+2\sqrt{2}\)

Những câu hỏi liên quan
1. dfrac{-2}{sqrt{3}-1}2. dfrac{5}{1-sqrt{6}}3. dfrac{2+sqrt{5}}{2-sqrt{5}}4. dfrac{1}{5+2sqrt{6}}5. dfrac{sqrt{5}+2}{sqrt{5}-2}6. dfrac{5sqrt{2}-2sqrt{5}}{sqrt{2}-sqrt{5}}7. dfrac{sqrt{20}-3sqrt{10}}{3-sqrt{2}}8. dfrac{6-2sqrt{5}}{3+sqrt{5}}9. dfrac{9+4sqrt{5}}{sqrt{5}+2}
Đọc tiếp
1. \(\dfrac{-2}{\sqrt{3}-1}\)
2. \(\dfrac{5}{1-\sqrt{6}}\)
3. \(\dfrac{2+\sqrt{5}}{2-\sqrt{5}}\)
4. \(\dfrac{1}{5+2\sqrt{6}}\)
5. \(\dfrac{\sqrt{5}+2}{\sqrt{5}-2}\)
6. \(\dfrac{5\sqrt{2}-2\sqrt{5}}{\sqrt{2}-\sqrt{5}}\)
7. \(\dfrac{\sqrt{20}-3\sqrt{10}}{3-\sqrt{2}}\)
8. \(\dfrac{6-2\sqrt{5}}{3+\sqrt{5}}\)
9. \(\dfrac{9+4\sqrt{5}}{\sqrt{5}+2}\)
Rút gọn: ( 2,5 Điểm )A dfrac{sqrt{6+2sqrt{5}}}{sqrt{5}+1}+ dfrac{sqrt{5-2sqrt{6}}}{sqrt{3}-sqrt{2}}B dfrac{3}{sqrt{5}-2}+ dfrac{4}{sqrt{6}+sqrt{2}}+ dfrac{1}{sqrt{6}+sqrt{5}}C dfrac{1}{sqrt{1}+sqrt{2}}+dfrac{1}{sqrt{2}+sqrt{3}}+dfrac{1}{sqrt{3}+sqrt{4}}+...+dfrac{1}{sqrt{99}+sqrt{100}}D dfrac{1}{2-sqrt{3}}+sqrt{7-4sqrt{3}}E sqrt{dfrac{3sqrt{3}-4}{2sqrt{3}+1}}-sqrt{dfrac{sqrt{3}+4}{5-2sqrt{3}}}F dfrac{1}{2+sqrt{3}}+dfrac{sqrt{2}}{sqrt{6}}-dfrac{2}{3+sqrt{3}}
Đọc tiếp
Rút gọn: ( 2,5 Điểm )
A= \(\dfrac{\sqrt{6+2\sqrt{5}}}{\sqrt{5}+1}\)+ \(\dfrac{\sqrt{5-2\sqrt{6}}}{\sqrt{3}-\sqrt{2}}\)
B= \(\dfrac{3}{\sqrt{5}-2}\)+ \(\dfrac{4}{\sqrt{6}+\sqrt{2}}\)+ \(\dfrac{1}{\sqrt{6}+\sqrt{5}}\)
C = \(\dfrac{1}{\sqrt{1}+\sqrt{2}}+\dfrac{1}{\sqrt{2}+\sqrt{3}}+\dfrac{1}{\sqrt{3}+\sqrt{4}}+...+\dfrac{1}{\sqrt{99}+\sqrt{100}}\)
D= \(\dfrac{1}{2-\sqrt{3}}+\sqrt{7-4\sqrt{3}}\)
E = \(\sqrt{\dfrac{3\sqrt{3}-4}{2\sqrt{3}+1}}-\sqrt{\dfrac{\sqrt{3}+4}{5-2\sqrt{3}}}\)
F = \(\dfrac{1}{2+\sqrt{3}}+\dfrac{\sqrt{2}}{\sqrt{6}}-\dfrac{2}{3+\sqrt{3}}\)
a: \(E=1+1=2\)
b: \(=6+3\sqrt{5}+\sqrt{6}-\sqrt{2}+\sqrt{6}-\sqrt{5}\)
\(=6+2\sqrt{6}-\sqrt{2}+2\sqrt{5}\)
d: \(=2+\sqrt{3}+2-\sqrt{3}=4\)
Đúng 1
Bình luận (0)
Tính:1) dfrac{3}{1-sqrt{2}}+dfrac{sqrt{2}-1}{sqrt{2}+1}2) dfrac{sqrt{5}-1}{sqrt{5}+1}+dfrac{6}{1-sqrt{5}}3) dfrac{sqrt{2}+sqrt{3}}{2-sqrt{6}}+dfrac{sqrt{3}-sqrt{2}}{sqrt{6}+2}4) dfrac{3+sqrt{3}}{sqrt{3}}+dfrac{sqrt{6}-sqrt{3}}{1-sqrt{2}}5) dfrac{2-sqrt{2}}{1-sqrt{2}}+dfrac{sqrt{2}-sqrt{6}}{sqrt{3}-1}
Đọc tiếp
Tính:
1) \(\dfrac{3}{1-\sqrt{2}}+\dfrac{\sqrt{2}-1}{\sqrt{2}+1}\)
2) \(\dfrac{\sqrt{5}-1}{\sqrt{5}+1}+\dfrac{6}{1-\sqrt{5}}\)
3) \(\dfrac{\sqrt{2}+\sqrt{3}}{2-\sqrt{6}}+\dfrac{\sqrt{3}-\sqrt{2}}{\sqrt{6}+2}\)
4) \(\dfrac{3+\sqrt{3}}{\sqrt{3}}+\dfrac{\sqrt{6}-\sqrt{3}}{1-\sqrt{2}}\)
5) \(\dfrac{2-\sqrt{2}}{1-\sqrt{2}}+\dfrac{\sqrt{2}-\sqrt{6}}{\sqrt{3}-1}\)
5: Ta có: \(\dfrac{2-\sqrt{2}}{1-\sqrt{2}}+\dfrac{\sqrt{2}-\sqrt{6}}{\sqrt{3}-1}\)
\(=-\sqrt{2}-\sqrt{2}\)
\(=-2\sqrt{2}\)
Đúng 0
Bình luận (0)
x^3left(sqrt[3]{5+2sqrt{6}}+sqrt[3]{5-2sqrt{6}}right)^3sqrt[3]{5+2sqrt{6}}^3+3sqrt[3]{left(5+2sqrt{6}right)^2}.sqrt[3]{5-2sqrt{6}}+3sqrt[3]{5+2sqrt{6}}.sqrt[3]{left(5-2sqrt{6}right)^2}+sqrt[3]{5-2sqrt{6}}^35+2sqrt{6}+3sqrt[3]{left(5+2sqrt{6}right)left(5-2sqrt{6}right)}.sqrt[3]{5+2sqrt{6}}+3sqrt[3]{left(5+2sqrt{6}right)left(5-2sqrt{6}right)}.sqrt[3]{5-2sqrt{6}}+5-2sqrt{6}5+5+3sqrt[3]{left(25-4.6right)}.sqrt[3]{5+2sqrt{6}}+3sqrt[3]{left(25-4.6right)}.sqrt[3]{5-2sqrt{6}}10+
3sqrt[3]{5+2sqrt{6}}+3sq...
Đọc tiếp
\(x^3=\left(\sqrt[3]{5+2\sqrt{6}}+\sqrt[3]{5-2\sqrt{6}}\right)^3=\sqrt[3]{5+2\sqrt{6}}^3\)
\(+3\sqrt[3]{\left(5+2\sqrt{6}\right)^2}.\sqrt[3]{5-2\sqrt{6}}+3\sqrt[3]{5+2\sqrt{6}}.\sqrt[3]{\left(5-2\sqrt{6}\right)^2}+\sqrt[3]{5-2\sqrt{6}}^3\)
\(=5+2\sqrt{6}+3\sqrt[3]{\left(5+2\sqrt{6}\right)\left(5-2\sqrt{6}\right)}.\sqrt[3]{5+2\sqrt{6}}\)
\(+3\sqrt[3]{\left(5+2\sqrt{6}\right)\left(5-2\sqrt{6}\right)}.\sqrt[3]{5-2\sqrt{6}}+5-2\sqrt{6}\)
\(=5+5+3\sqrt[3]{\left(25-4.6\right)}.\sqrt[3]{5+2\sqrt{6}}+3\sqrt[3]{\left(25-4.6\right)}.\sqrt[3]{5-2\sqrt{6}}\)
\(=10+ 3\sqrt[3]{5+2\sqrt{6}}+3\sqrt[3]{5-2\sqrt{6}}\)
p/s : có bạn hỏi nên mình đăng , các bạn đừng report nhé
dfrac{2sqrt{30}}{sqrt{5}+sqrt{6}+sqrt{7}}
sqrt{24}+6sqrt{dfrac{2}{3}+dfrac{10}{sqrt{6}-1}}dfrac{2sqrt{15}+sqrt{16}}{sqrt{84}+sqrt{6}}2sqrt{40sqrt{2}}-2sqrt{sqrt{75}}-3sqrt{5sqrt{48}} dfrac{left(2+sqrt{3}right)^2-1}{left(sqrt{3}+1right)^2}:dfrac{left(3+sqrt{5}right)^2-4}{left(sqrt{5}+1right)^2}giúp em với ạ
Đọc tiếp
\(\dfrac{2\sqrt{30}}{\sqrt{5}+\sqrt{6}+\sqrt{7}} \)
\(\sqrt{24}+6\sqrt{\dfrac{2}{3}+\dfrac{10}{\sqrt{6}-1}}\)
\(\dfrac{2\sqrt{15}+\sqrt{16}}{\sqrt{84}+\sqrt{6}}\)
\(2\sqrt{40\sqrt{2}}-2\sqrt{\sqrt{75}}-3\sqrt{5\sqrt{48}}\)
\(\dfrac{\left(2+\sqrt{3}\right)^2-1}{\left(\sqrt{3}+1\right)^2}:\dfrac{\left(3+\sqrt{5}\right)^2-4}{\left(\sqrt{5}+1\right)^2}\)
giúp em với ạ
\(2\sqrt{40\sqrt{3}}-2\sqrt{\sqrt{75}}-3\sqrt{5\sqrt{48}}\)
\(=2\cdot\sqrt{40\sqrt{3}}-2\cdot\sqrt{5\sqrt{3}}-3\cdot\sqrt{20\sqrt{3}}\)
\(=2\cdot2\sqrt{10}\cdot\sqrt{\sqrt{3}}-2\cdot\sqrt{5}\cdot\sqrt{\sqrt{3}}-6\sqrt{5}\cdot\sqrt{\sqrt{3}}\)
\(=4\sqrt{10}\sqrt{\sqrt{3}}-4\cdot\sqrt{5}\cdot\sqrt{\sqrt{3}}\)
Đúng 0
Bình luận (0)
MÌNH CẦN LUÔN ẠRút gọn biểu thức:1(2+sqrt{3})(7-4sqrt{3})2)left(sqrt{5-2sqrt{6}}+sqrt{2}right)sqrt{3}3)sqrt{4+2sqrt{3}}-sqrt{5-2sqrt{6}}+sqrt{2}4)sqrt{3+2sqrt{2}}+sqrt{6-4sqrt{2}}5)2+sqrt{17-4sqrt{9+4sqrt{5}}}
Đọc tiếp
MÌNH CẦN LUÔN Ạ![]()
Rút gọn biểu thức:
1(2+\(\sqrt{3}\))(7-4\(\sqrt{3}\))
2)\(\left(\sqrt{5-2\sqrt{6}}+\sqrt{2}\right)\sqrt{3}\)
3)\(\sqrt{4+2\sqrt{3}}-\sqrt{5-2\sqrt{6}}+\sqrt{2}\)
4)\(\sqrt{3+2\sqrt{2}}+\sqrt{6-4\sqrt{2}}\)
5)\(2+\sqrt{17-4\sqrt{9+4\sqrt{5}}}\)
\(1,\left(2+\sqrt{3}\right)\left(7-4\sqrt{3}\right)\\ =14-8\sqrt{3}+7\sqrt{3}-12\\ =2-\sqrt{3}\\ 2,\left(\sqrt{5-2\sqrt{6}}+\sqrt{2}\right)\sqrt{3}\\ =\left(\sqrt{\left(\sqrt{3}-\sqrt{2}\right)^2}+\sqrt{2}\right)\sqrt{3}\\ =\left(\left|\sqrt{3}-\sqrt{2}\right|+\sqrt{2}\right)\sqrt{3}\\ =\left(\sqrt{3}-\sqrt{2}+\sqrt{2}\right)\sqrt{3}\\ =\sqrt{3}.\sqrt{3}\\ =3\\ 3,\sqrt{4+2\sqrt{3}}-\sqrt{5-2\sqrt{6}}+\sqrt{2}\\ =\sqrt{\left(\sqrt{3}+1\right)^2}-\sqrt{\left(\sqrt{3}-\sqrt{2}\right)^2}+\sqrt{2}\\ =\left|\sqrt{3}+1\right|-\left|\sqrt{3}-\sqrt{2}\right|+\sqrt{2}\\ =\sqrt{3}+1-\sqrt{3}-\sqrt{2}+\sqrt{2}\\ =1\\ 4,\sqrt{3+2\sqrt{2}}+\sqrt{6-4\sqrt{2}}\\ =\sqrt{\left(1+\sqrt{2}\right)^2}+\sqrt{\left(\sqrt{4}-\sqrt{2}\right)^2}\\ =\left|1+\sqrt{2}\right|+\left|\sqrt{4}-\sqrt{2}\right|\\ =1+\sqrt{2}+\sqrt{4}-\sqrt{2}\\ =1+\sqrt{4}\\ 5,2+\sqrt{17-4\sqrt{9+4\sqrt{5}}}\\ =2+\sqrt{17-8-4\sqrt{5}}\\ =2+\sqrt{\left(\sqrt{5}-2\right)^2}\\ =2+\left|\sqrt{5}-2\right|\\ =2+\sqrt{5}-2\\ =\sqrt{5}\)
Đúng 1
Bình luận (0)
1. Tính
a) \(\sqrt[3]{(\sqrt{2}+3)(11+6\sqrt{2})}\sqrt[3]{(\sqrt{2}+-3)(11-6\sqrt{2})}\)
b) (\((\sqrt[3]{9}+\sqrt[3]{6}+\sqrt[3]{4})(\sqrt[3]{3}-\sqrt[3]{2})\)
c)\(\sqrt[3]{2+\sqrt{5}}+\sqrt[3]{2-\sqrt{5}}\)
\(a:\sqrt{\left(\sqrt{3}-2\right)^2}+\sqrt{5+2\sqrt{6}}\)
b : \(\dfrac{\sqrt{6}-\sqrt{2}}{\sqrt{3}-1}-\sqrt{2}\)
c : \(\left(2+\dfrac{5-2\sqrt{5}}{2-\sqrt{5}}\right).\left(2+\dfrac{5-3\sqrt{5}}{3-\sqrt{5}}\right)\)
d : \(\left(\dfrac{15}{\sqrt{6}+1}+\dfrac{4}{\sqrt{6}-2}-\dfrac{12}{3-\sqrt{6}}\right).\left(\sqrt{6}+11\right)\)
a) \(\sqrt{\left(\sqrt{3}-2\right)^2}+\sqrt{5+2\sqrt{6}}\)
\(=\left|\sqrt{3}-2\right|+\sqrt{\left(\sqrt{3}\right)^2+2\cdot\sqrt{3}\cdot\sqrt{2}+\left(\sqrt{2}\right)^2}\)
\(=\left(\sqrt{3}-\sqrt{2}\right)+\sqrt{\left(\sqrt{3}+\sqrt{2}\right)^2}\)
\(=\sqrt{3}-\sqrt{2}+\sqrt{3}+\sqrt{2}\)
\(=2\sqrt{3}\)
b) \(\dfrac{\sqrt{6}-\sqrt{2}}{\sqrt{3}-1}-\sqrt{2}\)
\(=\dfrac{\sqrt{2}\left(\sqrt{3}-1\right)}{\sqrt{3}-1}-\sqrt{2}\)
\(=\sqrt{2}-\sqrt{2}\)
\(=0\)
c) \(\left(2+\dfrac{5-2\sqrt{5}}{2-\sqrt{5}}\right)\cdot\left(2+\dfrac{5-3\sqrt{5}}{3-\sqrt{5}}\right)\)
\(=\left[2-\dfrac{\sqrt{5}\left(2-\sqrt{5}\right)}{2-\sqrt{5}}\right]\cdot\left[2-\dfrac{\sqrt{5}\left(3-\sqrt{5}\right)}{3-\sqrt{5}}\right]\)
\(=\left(2-\sqrt{5}\right)\left(2-\sqrt{5}\right)\)
\(=4-4\sqrt{5}+5\)
\(=9-4\sqrt{5}\)
d) \(\left(\dfrac{15}{\sqrt{6}+1}+\dfrac{4}{\sqrt{6}-2}-\dfrac{12}{3-\sqrt{6}}\right)\left(\sqrt{6}+11\right)\)
\(=\left[\dfrac{15\left(\sqrt{6}-1\right)}{\left(\sqrt{6}+1\right)\left(\sqrt{6}-1\right)}+\dfrac{4\left(\sqrt{6}+2\right)}{\left(\sqrt{6}-2\right)\left(\sqrt{6}+2\right)}-\dfrac{12\left(3+\sqrt{6}\right)}{\left(3-\sqrt{6}\right)\left(3+\sqrt{6}\right)}\right]\left(\sqrt{6}+11\right)\)
\(=\left[\dfrac{15\left(\sqrt{6}-1\right)}{5}+\dfrac{4\left(\sqrt{6}+2\right)}{6-4}-\dfrac{12\left(3+\sqrt{6}\right)}{9-6}\right]\left(\sqrt{6}+11\right)\)
\(=\left(3\sqrt{6}-3+2\sqrt{6}+4-12-4\sqrt{6}\right)\left(\sqrt{6}+11\right)\)
\(=\left(\sqrt{6}-11\right)\left(\sqrt{6}+11\right)\)
\(=6-121\)
\(=-115\)
Đúng 1
Bình luận (0)
* Thực hiện phép tính:
a. \(\dfrac{\sqrt{7}-5}{2}-\dfrac{6-2\sqrt{7}}{4}+\dfrac{6}{\sqrt{7}-2}-\dfrac{5}{4+\sqrt{7}}\)
b. \(\dfrac{2}{\sqrt{6}-2}+\dfrac{2}{\sqrt{6}+2}+\dfrac{5}{\sqrt{6}}\)
c. \(\dfrac{1}{\sqrt{3}+\sqrt{2}-\sqrt{5}}-\dfrac{1}{\sqrt{3}+\sqrt{2}+\sqrt{5}}\)
\(a,=\dfrac{\sqrt{7}-5}{2}-\dfrac{3-\sqrt{7}}{2}+\dfrac{6\left(\sqrt{7}+2\right)}{3}-\dfrac{5\left(4-\sqrt{7}\right)}{9}\\ =\dfrac{\sqrt{7}-5-3+\sqrt{7}}{2}+2\sqrt{7}+4-\dfrac{20-5\sqrt{7}}{9}\\ =\dfrac{2\sqrt{7}-8}{2}+2\sqrt{7}+4-\dfrac{20-5\sqrt{7}}{9}\\ =\sqrt{7}-4+2\sqrt{7}+4-\dfrac{20-5\sqrt{7}}{9}\\ =\dfrac{27\sqrt{7}-20+5\sqrt{7}}{9}=\dfrac{32\sqrt{7}-20}{9}\)
\(b,=\dfrac{2\left(\sqrt{6}+2\right)}{2}+\dfrac{2\left(\sqrt{6}-2\right)}{2}+\dfrac{5\sqrt{6}}{6}\\ =\sqrt{6}+2+\sqrt{6}-2+\dfrac{5\sqrt{6}}{6}\\ =\dfrac{12\sqrt{6}+5\sqrt{6}}{6}=\dfrac{17\sqrt{6}}{6}\)
\(c,=\dfrac{\sqrt{3}+\sqrt{2}+\sqrt{5}-\sqrt{3}-\sqrt{2}+\sqrt{5}}{\left(\sqrt{3}+\sqrt{2}\right)^2-5}\\ =\dfrac{2\sqrt{5}}{5+2\sqrt{6}-5}=\dfrac{2\sqrt{5}}{2\sqrt{6}}=\dfrac{\sqrt{30}}{6}\)
Đúng 2
Bình luận (0)
frac{3+2sqrt{3}}{sqrt{3}}+frac{2+sqrt{2}}{sqrt{2}+1}-left(sqrt{2}+3right)
0.1cdotsqrt{left(-3right)^2}cdotleft[6sqrt{left(frac{1}{3}right)^2}-sqrt{left(sqrt{3}-2right)^2}right]^2
left(frac{3sqrt{2}+sqrt{6}}{sqrt{12}+2}-frac{sqrt{54}}{3}right)cdotfrac{2}{sqrt{6}}
left(frac{3+2sqrt{3}}{sqrt{3}+2}+frac{2+sqrt{2}}{sqrt{2}+1}right)divleft(1divfrac{1}{sqrt{2}+sqrt{3}}right)
sqrt{frac{5+2sqrt{6}}{5-2sqrt{6}}}+sqrt{frac{5-2sqrt{6}}{5+2sqrt{6}}}
Đọc tiếp
\(\frac{3+2\sqrt{3}}{\sqrt{3}}+\frac{2+\sqrt{2}}{\sqrt{2}+1}-\left(\sqrt{2}+3\right)\)
\(0.1\cdot\sqrt{\left(-3\right)^2}\cdot\left[6\sqrt{\left(\frac{1}{3}\right)^2}-\sqrt{\left(\sqrt{3}-2\right)^2}\right]^2\)
\(\left(\frac{3\sqrt{2}+\sqrt{6}}{\sqrt{12}+2}-\frac{\sqrt{54}}{3}\right)\cdot\frac{2}{\sqrt{6}}\)
\(\left(\frac{3+2\sqrt{3}}{\sqrt{3}+2}+\frac{2+\sqrt{2}}{\sqrt{2}+1}\right)\div\left(1\div\frac{1}{\sqrt{2}+\sqrt{3}}\right)\)
\(\sqrt{\frac{5+2\sqrt{6}}{5-2\sqrt{6}}}+\sqrt{\frac{5-2\sqrt{6}}{5+2\sqrt{6}}}\)