
 Giải dùm đi mọi người
Giải dùm đi mọi người

Những câu hỏi liên quan
Giải hôn dùm mình đi mọi người ơi

1 C
2 C
3 D
4 A
5 D
6 D
7
8 A
9 C
10 D
( Câu 7 đáp án sai hay sao á bạn )
Đúng 0
Bình luận (3)
Mọi người ơi ai biết giải dùm mik đi ạ mik đang cần gấp lắm
Bài 1:
a) Ta có:
\(a=\dfrac{v-v_0}{t-t_0}=\dfrac{10-50}{20}=-2\) (m/\(s^2\))
=> PTCĐ: \(x=x_0+v_0t+\dfrac{1}{2}at^2\)
\(\Leftrightarrow\) \(x=50t+\dfrac{1}{2}.\left(-2\right).t^2\)
\(\Leftrightarrow\) \(x=50t-t^2\)
b) Quảng đường vật đi được:
\(S=v_0+\dfrac{1}{2}at^2\)\(=50.20+\dfrac{1}{2}.\left(-2\right).20^2=600\) (m)
Đúng 0
Bình luận (0)
giải dùm bài 159sbt/76 toán 8 hình học cho e đi mọi người
giải dùm mk bài này đi mọi người
Thay số để
a, * * * * 9 chia hết cho 1192 *
b, abcd0 - abcd = 2261 *
Mọi người giải dùm mình với
mọi người giải dùm em vs ạ bạn em nhờ em hỏi dùm
em cảm ơn nhiều
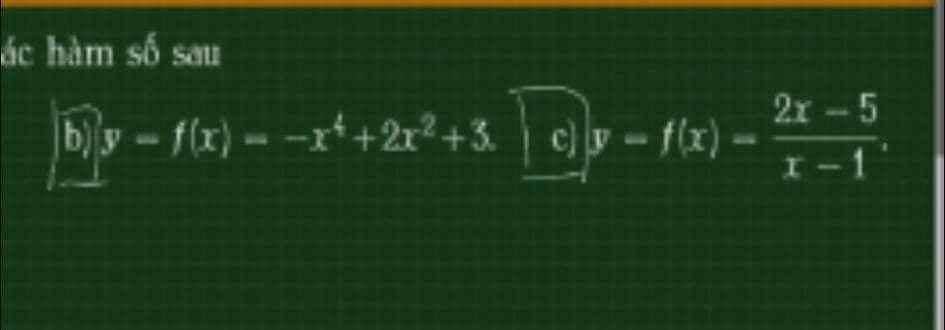

cái hồi nãy thiếu câu hỏi em bổ sung ở dưới này ạ
em cảm ơn mn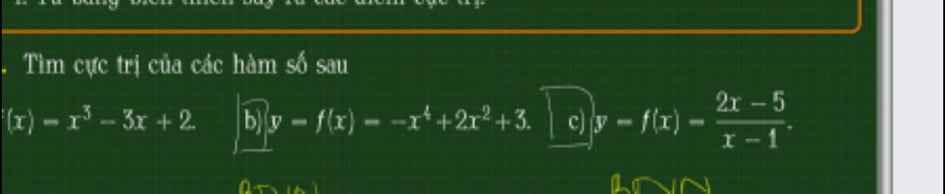
Đúng 0
Bình luận (1)
5.
TXĐ: \(D=\left(-\infty;-1\right)\cup\left(-1;+\infty\right)\)
\(y'=\dfrac{2}{\left(x+1\right)^2}>0\) ; \(\forall x\in D\)
\(\Rightarrow\) Hàm đồng biến trên mỗi khoảng xác định
Hay hàm đồng biến trên \(\left(-\infty;-1\right)\) và \(\left(-1;+\infty\right)\)
6.
\(y=4x^3-4x=0\Rightarrow\left[{}\begin{matrix}x=0\\x=-1\\x=1\end{matrix}\right.\)
Dấu của y' trên trục số:
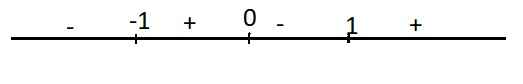
Từ đó ta thấy:
Hàm đồng biến trên các khoảng \(\left(-1;0\right)\) và \(\left(1;+\infty\right)\)
Hàm nghịch biến trên các khoảng \(\left(-\infty;-1\right)\) và \(\left(1;+\infty\right)\)
Đúng 0
Bình luận (0)
Tìm cực trị
a.
\(f'\left(x\right)=3x^2-3=0\Rightarrow x=\pm1\)
\(f''\left(x\right)=6x\)
\(f''\left(-1\right)=-6< 0\)
\(f''\left(1\right)=6>0\)
\(\Rightarrow x=-1\) là điểm cực đại và \(x=1\) là điểm cực tiểu
b.
\(f'\left(x\right)=-4x^3+4x=0\Rightarrow\left[{}\begin{matrix}x=0\\x=-1\\x=1\end{matrix}\right.\)
\(f''\left(x\right)=-12x^2+4\)
\(f''\left(0\right)=4>0\) ; \(f''\left(-1\right)=-8< 0\) ; \(f''\left(1\right)=-8< 0\)
\(\Rightarrow x=0\) là điểm cực tiểu và \(x=\pm1\) là 2 điểm cực đại
c.
\(f'\left(x\right)=\dfrac{3}{\left(x-1\right)^2}\ne0\) với mọi x thuộc miền xác định
Hàm không có cực trị
Đúng 0
Bình luận (0)
Nhờ mọi người giải dùm em gấp ạ
 mọi người giải rõ ràng ra dùm mình với
mọi người giải rõ ràng ra dùm mình với
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{36}=\dfrac{b}{38}=\dfrac{a+b}{36+38}=\dfrac{222}{74}=3\)
Do đó: a=108; b=114
Đúng 0
Bình luận (0)
\(\text{Gọi x;y lần lượt là số dây đeo khẩu trang lớp 7A,7B:}\)
(đk:x;y\(\in\)N*,đơn vị:dây đeo khẩu trang)
\(\text{Ta có:}\dfrac{x}{36}=\dfrac{y}{38}\text{ và }x+y=222\)
\(\text{Áp dụng tính chất dãy tỉ số bằng nhau:}\)
\(\dfrac{x}{36}=\dfrac{y}{38}=\dfrac{x+y}{36+38}=\dfrac{222}{74}=3\)
\(\Rightarrow x=3.36=108\text{(dây đeo khẩu trang)}\)
\(y=3.38=114\text{(dây đeo khẩu trang)}\)
\(\text{Vậy số dây đeo khẩu trang lớp 7A là:108 dây đeo khẩu trang}\)
\(\text{lớp 7B là:114 dây đeo khẩu trang}\)
Đúng 0
Bình luận (0)
mọi người giải giúp em câu 71,74 với
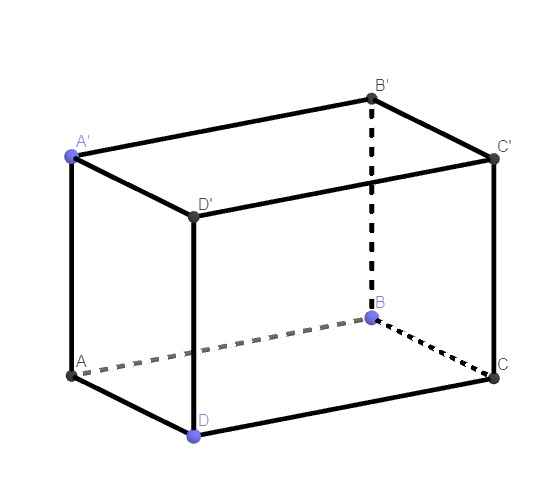
em cảm ơn mọi người nhiều vẽ hình dùm em luôn em cảm ơn
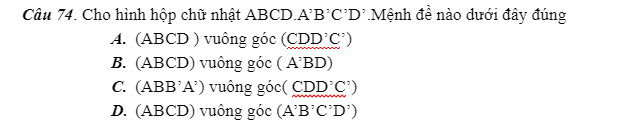
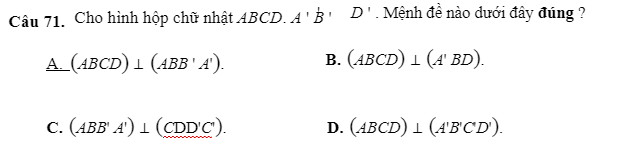
71.
\(\left\{{}\begin{matrix}BB'\perp\left(ABCD\right)\\BB'\in\left(ABB'A'\right)\end{matrix}\right.\) \(\Rightarrow\left(ABCD\right)\perp\left(ABB'A'\right)\)
74.
\(\left\{{}\begin{matrix}DD'\perp\left(ABCD\right)\\DD'\in\left(CDD'C'\right)\end{matrix}\right.\) \(\Rightarrow\left(ABCD\right)\perp\left(CDD'C'\right)\)
Đúng 0
Bình luận (0)


















