Cho \(\triangle ABC\), dựng \(MN//BC\) như hình sau. Biết rằng \(\widehat{ABx}=100^{0},\widehat{MNC}=140^{0}\). Tính số đo góc \(\widehat{BAC}\).

Trình bày lời giải rõ ràng nhé! Cảm ơn! (^_^)
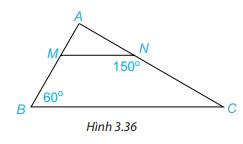
1. Cho Hình 3.36, biết MN//BC, \(\widehat {ABC} = 60^\circ ,\widehat {MNC} = 150^\circ \).
Hãy tính số đo các góc BMN và ACB.
2. Cho Hình 3.37, biết rằng xx’//yy’ và zz’ \( \bot \) xx’. Tính số đo góc ABy và cho biết zz’ có vuông góc với yy’ không?

1. Vì MN//BC nên \(\widehat {AMN} = \widehat {ABC}\)( 2 góc đồng vị), mà \(\widehat {ABC} = 60^\circ \)nên \(\widehat {AMN} = 60^\circ \)
Vì \(\widehat {AMN} + \widehat {BMN} = 180^\circ \) (2 góc kề bù)
\(\begin{array}{l} \Rightarrow 60^\circ + \widehat {BMN} = 180^\circ \\ \Rightarrow \widehat {BMN} = 180^\circ - 60^\circ = 120^\circ \end{array}\)
Vì \(\widehat {ANM} + \widehat {MNC} = 180^\circ \)(2 góc kề bù)
\(\begin{array}{l} \Rightarrow \widehat {ANM} + 150^\circ = 180^\circ \\ \Rightarrow \widehat {ANM} = 180^\circ - 150^\circ = 30^\circ \end{array}\)
Vì MN//BC nên \(\widehat {ANM} = \widehat {ACB}\) ( 2 góc đồng vị), mà \(\widehat {ANM} = 30^\circ \)nên \(\widehat {ACB} = 30^\circ \).
2. Vì xx’//yy’ nên \(\widehat {x'AB} = \widehat {ABy}\)( 2 góc so le trong)
Mà zz’\( \bot \) xx’ nên \(\widehat {x'AB} = 90^\circ \)
Do đó, \(\widehat {ABy} = 90^\circ \) nên zz’ vuông góc với yy’.
Cho hình chóp S.ABC có SA \( \bot \) (ABC), AB = AC = a, \(\widehat {BAC} = {120^0},SA = \frac{a}{{2\sqrt 3 }}.\) Gọi M là trung điểm của BC.
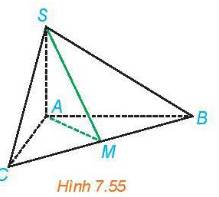
a) Chứng minh rằng \(\widehat {SMA}\) là một góc phẳng của góc nhị diện \(S, BC, A].
b) Tính số đo của góc nhị diện \(S, BC, A].
a) Xét tam giác ABC có AB = AC => tam giác ABC cân tại A mà M là trung điểm BC
=> \(AM \bot BC\) (1)
\(\begin{array}{l}SA \bot BC\left( {SA \bot \left( {ABCD} \right)} \right)\\ \Rightarrow BC \bot \left( {SAM} \right);SM \subset \left( {SAM} \right) \Rightarrow BC \bot SM\,\,\,\left( 2 \right)\end{array}\)
Từ (1), (2) ta có \(\widehat {SMA}\) là một góc phẳng của góc nhị diện [S, BC, A].
b) Xét tam giác ABC cân tại A có
\(\widehat {BAC} = {120^0} \Rightarrow \widehat {ACB} = {30^0}\)
\(\sin \widehat {ACB} = \frac{{AM}}{{AC}} \Leftrightarrow \tan {30^0} = \frac{{AM}}{a} \Leftrightarrow AM = \frac{a}{{\sqrt 3 }}\)
\(\tan \widehat {SMA} = \frac{{SA}}{{AM}} = \frac{a}{{2\sqrt 3 }}:\frac{a}{{\sqrt 3 }} = \frac{1}{2} \Rightarrow \widehat {SMA} = \arctan \frac{1}{2}\)
Cho ΔBCD. Trên nửa mặt phẳng có bờ BD chứa điểm C vẽ tia BA. Vẽ tia Bx là tia đối của tia BD. Biết \(\widehat{C}\)= 420, \(\widehat{D}\)=750. Tính số đo các góc \(\widehat{ABx},\widehat{ABC},\widehat{CBD}\)
Cho tam giác ABC có \(\widehat{BAC}\)=\(60^0\), \(\widehat{BAC}\)< \(\widehat{ABC}\). Trong góc ABC vẽ tia Bx sao cho \(\widehat{CBx}\)= \(60^0\). Trên tia Bx lấy điểm D sao cho BD = BC. Tính số đo góc BAD .
Vẽ tam giác ABC biết \(\widehat{B}=90^0,BA=BC=2,5cm\). Sau đó đo các góc A và C để kiểm tra rằng \(\widehat{A}=\widehat{C}=45^0\)
Cho tam giác ABC,dựng MN//BC.Biết ABx=100 độ,MNC=140 độ.Tính BAC
Một khung cửa sổ hình tam giác có thiết kế như Hình 18a được vẽ lại như Hình 18b.
a) Cho biết \(\widehat {{A_1}}\)\( = {42^o}\). Tính số đo của \(\widehat {{M_1}}\),\(\widehat {{B_1}}\),\(\widehat {{M_2}}\).
b) Chứng minh MN // BC, MP // AC.
c) Chứng minh bốn tam giác cân AMN, MBP, PMN, NPC bằng nhau.
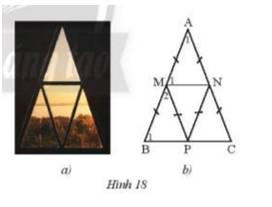
a) Ta thấy tam giác AMN cân tại A do AM = AN
\( \Rightarrow \widehat {{M_1}} = ({180^o} - \widehat {{A_1}}):2 = ({180^o} - {42^o}):2 = {69^o}\)
Ta thấy tam giác PMN = tam giác AMN ( c-c-c )
\( \Rightarrow \widehat {{M_1}} = \widehat {PMN} = {69^o}\) (góc tương ứng )
Mà \( \Rightarrow \widehat {{M_1}} + \widehat {{M_2}} + \widehat {PMN} = {180^o}\)( các góc kề bù )
\( \Rightarrow \widehat {{M_2}} = {180^o} - {69^o} - {69^o} = {42^o}\)
Mà tam giác MPB cân tại M do MB = MP nên
\( \Rightarrow \widehat {{B_1}} = \widehat {MPB}\)
Áp dụng định lí tổng 3 góc trong tam giác
\( \Rightarrow \widehat {{B_1}} = ({180^o} - {42^o}):2 = {69^o}\)
b) Ta thấy \(\widehat {{B_1}}\)và \(\widehat {{M_1}}\)ở vị trí đồng vị và bằng nhau nên
\( \Rightarrow \)MN⫽BC
Vì tam giác PMN = tam giác AMN nên ta có
\( \Rightarrow \widehat {{M_1}} = \widehat {ANM} = \widehat {PMN} = \widehat {MNP}\)( do 2 tam giác cân và bằng nhau )
Mà \(\widehat {MNA}\)và\(\widehat {PMN}\) ở vị trí so le trong
\( \Rightarrow \)MP⫽AC
c) Ta có \(\Delta AMN = \Delta PMN = \Delta MBP(c - g - c)\)(1)
Vì MP⫽AC ( chứng minh trên )
\( \Rightarrow \widehat {MPN} = \widehat {PNC}\) ( 2 góc so le trong ) =\({42^o}\)
\( \Rightarrow \Delta MPN = \Delta NCP(c - g - c)\)(2)
Từ (1) và (2) \( \Rightarrow \) 4 tam giác cân AMN, MBP, PMN, NCP bằng nhau
Cho tam giác ABC có \(\widehat{ABC}\) =\(55^0\),trên cạnh AC lấy điểm D(D không trùng với A và C).
a)Tính độ dài AC ,biết AD=4cm ,CD =3cm .
b)Tính số đo của \(\widehat{DBC}\), biết \(\widehat{ABD}\) =\(30^0\).
c)Từ B dựng tia Bx sao cho \(\widehat{DBx}\) \(=90^0\).Tính số đo\(\widehat{ABx}\)
d)Trên cạnh AB lấy điểm E (E không trùng với a và b).Chứng minh rằng hai đoạn thẳng BD và CE cắt nhau
a)độ dài đoạn AC=4+3=7cm
b)\(\widehat{DBC}\)sẽ bằng :55-30=25,vì \(\widehat{ABC}\)=55 độ mà \(\widehat{ABD}\)=33 độ nên \(\widehat{DBC}\)=55 độ
còn câu c,d mai mình giải.
a)+)Trên cạnh AC lấy điểm D
=>Điểm D nằm giữa 2 điểm A và C
=>AD+DC=AC
4 +3 =AC
7cm =AC
Vậy AC=7cm
b)+)Điểm D nằm giữa 2 điểm A và C
=>Tia BD nằm giữa 2 tia BA và BC(1)
=>\(\widehat{ABD}\)+\(\widehat{DBC}\)=\(\widehat{ABC}\)
=>30o+\(\widehat{DBC}\) =55o
\(\widehat{DBC}\) =55o-30o=25o
Vậy \(\widehat{DBC}\)=25o
c)+)Ta có 2 TH:(tự vẽ hình)
TH1:Tia Bx và BC cùng nằm trên một nửa mặt phẳng có bờ là đường thẳng chứa tia BD ta có:\(\widehat{DBC}< \widehat{DBx}\)(vì 25o<900)
=>Tia BC nằm giữa 2 tia Bx và BD(2)
+)Từ (1) và (2)
=>Tia BD nằm giữa 2 tia Bx và BA
=>\(\widehat{ABD}+\widehat{DBx}=\widehat{ABx}\)
=>30o +90o =\(\widehat{ABx}\)
=>120o =\(\widehat{ABx}\)
Vậy \(\widehat{ABx}\)=120o
TH2:+)Tia BA và Bx cùng nằm trên cùng một nửa mặt phẳng có bờ là đường thẳng chứa tia BD ta có:\(\widehat{DBA}< \widehat{DBx}\)(vì 30o<90o)
=>Tia BA nằm giữa 2 tia BD và Bx
=>\(\widehat{DBA}+\widehat{ABx}=\widehat{DBx}\)
=>30o +\(\widehat{ABx}\)=90o
\(\widehat{ABx}\)=90o-30o=60o
Vậy \(\widehat{ABx}\)600
Chúc bn học tốt
Cho tam giác ABC vuông tại A, biết \(\widehat{B}=4\widehat{C}\). Tìm số đo của góc B
\(A.\widehat{B}=72^0\) \(B.\widehat{B}=18^0\) \(C.\widehat{B}=48^0\) \(D.\widehat{B}=64^0\)