b: Xét tứ giác ADME có 

\(\widehat{ADM}=\widehat{AEM}=\widehat{EAD}=90^0\)

Do đó: ADME là hình chữ nhật

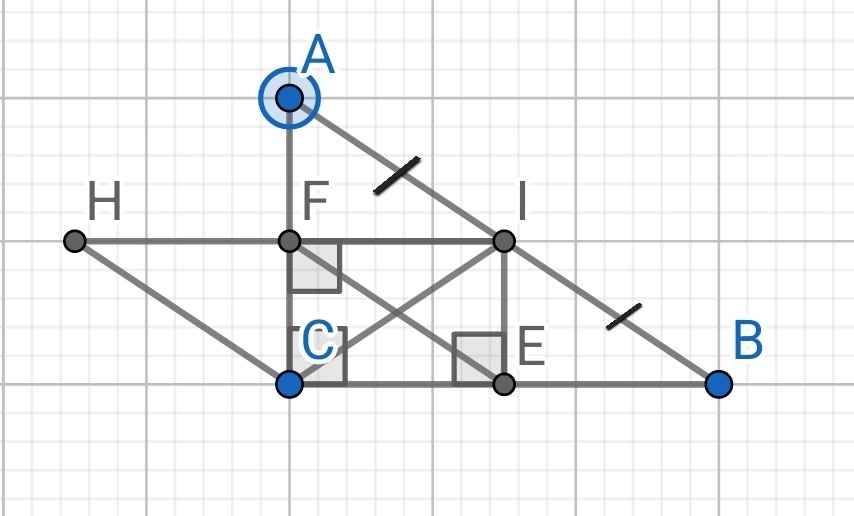   *) Tứ giác CEIF là hình gì?

Tứ giác CEIF có:

∠CEI = ∠CFI = ∠ECF = 90⁰ (gt)

⇒ CEIF là hình chữ nhật

*) Do CEIF là hình chữ nhật (cmt)

⇒ FI = CE và FI // CE

Do FI // CE (cmt)

⇒ FH // CE

Do FI = CE (cmt)

FI = FH (gt)

⇒ FH = CE

Tứ giác CHFE có:

FH // CE (cmt)

FH = CE (cmt)

⇒ CHFE là hình bình hành

Sửa đề: IF vuông góc AC tại F

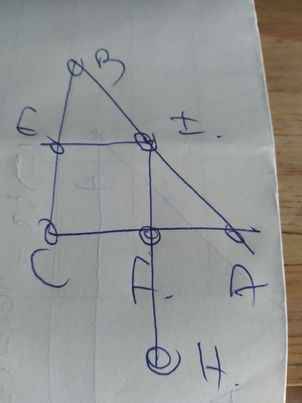
a: Xét tứ giác CEIF có

\(\widehat{CEI}=\widehat{CFI}=\widehat{FCE}=90^0\)

Do đó: CEIF là hình chữ nhật

b: CEIF là hình chữ nhật

=>CE//FI và CE=FI

CE=FI

FI=FH

Do đó: CE=FH

CE//FI

\(F\in IH\)

Do đó: CE=FH

Xét tứ giác CEFH có

CE//FH

CE=FH

Do đó: CEFH là hình bình hành

a ) Xét ◇DENF có :

Góc N = Góc F = Ê = 90°

⇒◇DENF là hình chữ nhật

b ) Trong ΔMNP có : ND là đường trung tuyến 

⇒ND = DP ( vì đường trung tuyến bằng nữa cạnh huyền )

Xét ΔNDF và ΔPDF có :

⇒ΔNDF = ΔPDF ( cạnh huyền - cạnh góc vuông )

⇒NF = PF ( 2 cạnh tương ứng )

⇒F là trung điểm NP

a: Xét ΔABC có

M,N lần lượt là trung điểm của AB và AC

nên MN là đường trung bình

=>MN//BC và MN=BC/2

=>MN//BE và MN=BE

=>BMNE là hình bình hành

b: Ta có: ΔAHB vuông tại H

mà HM là đường trung tuyến

nên HM=AM(1)

Ta có: ΔAHC vuông tại H

mà HN là đường trung tuyến

nên HN=AN(2)

Từ (1)và (2) suy ra AH là đường trung trực của MN

Xét ΔABC có 

E,M lần lượt là trung điểm của CB và BA

nên ME là đường trung bình

=>ME=CA/2=NH

Xét tứ giác MNEH có MN//EH

nên MNEH là hình thang

mà ME=NH

nên MNEH là hình thang cân

a: Xét tứ giác AEIF có 

\(\widehat{AEI}=\widehat{AFI}=\widehat{FAE}=90^0\)

Do đó: AEIF là hình chữ nhật

a: Xét ΔABC có

M là trung điểm của BA
N là trung điểm của AC

Do đó: MN là đường trung bình

=>MN//BC và MN=BC/2

=>MN=BE và MN//BE

=>BMNE là hình bình hành

b: Ta có: ΔAHB vuông tại H

mà HM là đường trung tuyến

nên HM=AM

=>M nằm trên đường trung trực của AH(1)

Ta có: ΔAHC vuông tại H

mà HN là đường trung tuyến

nên HN=AC/2=AN

=>N nằm trên đường trung trực của AH(2)

Từ (1) và (2) suy ra MN là đường trung trực của AH

Xét ΔABC có 

M là trung điểm của AB

E là trung điểm của BC

Do đó: ME là đường trung bình

=>ME=AC/2

mà HN=AC/2

nên ME=HN

Xét tứ giác MNEH có MN//EH

nên MNEH là hình thang

mà ME=NH

nên MNEH là hình thang cân

e) Chứng minh HI, ST, KF đồng quy.

Gọi O là giao điểm của EI và HK.

Xét tứ giác HIKE ta có:

góc IHE = 90⁰ (HI _|_ EB tại H)

góc IKE = 90⁰ (KI _|_ EC tại K)

góc HEK = 90⁰ (tứ giác ABEC là hình chữ nhật)

=> tứ giác HIKE là hình chữ nhật (tứ giác có 3 góc vuông)

=> góc HIK = 90⁰

=> KI _|_ HI tại I

Xét hình chữ nhật HIKE ta có:

2 đường chéo EI và HK cắt nhau tại O (cách vẽ)

=> O là trung điểm của EI và O là trung điểm của HK

Xét tam giác FEI vuông tại F ta có:

FO là đường trung tuyến ứng với cạnh huyền EI (O là trung điểm của EI)

=> FO = 1/2 EI

Mà EI = HK (tứ giác HIKE là hình chữ nhật)

Nên FO = 1/2 Hk

Xét tam giác FHK ta có:

FO là đường trung tuyến (O là trung điểm của HK)

FO = 1/2 HK (cmt)

=> tam giác FHK vuông tại F

=> HF _|_ FK tại F

Xét tam giác SHK ta có:

ST là đường cao (ST _|_ HK tại T)

HI là đường cao (HI _|_ KI tại I)

KF là đường cao (KF _|_ HF tại F)

=> HI, ST, KF đồng quy tại một điểm (đpcm)

làm dài v mà có 1 người nhận xét đúng làm làm j