Tìm x để P(x) là mệnh đề đúng:
a. P(x): x2 - 3x > 0"
b. P(x): "\(\sqrt{x}\) lớn hơn hoặc bằng x"
Những câu hỏi liên quan
Cho mệnh đề chứa biến P(x), với x \(\in R\). Tìm x để P(x) là mệnh đề đúng?
a) P(x): " \(x^2-5x+4=0\) "
b) P(x): " \(x^2-5x+6=0\) "
c) P(x): " \(x^2-3x>0\) "
d) P(x): "\(\sqrt{x}>x\) "
e) P(x): " 2x+ 3<7 "
f) P(x): " \(x^2+x+1>0\) "
d) \(\sqrt[]{x}>x\)
\(\Leftrightarrow x-\sqrt[]{x}< 0\)
\(\Leftrightarrow\sqrt[]{x}\left(\sqrt[]{x}-1\right)< 0\left(x\ge0\right)\)
\(\Leftrightarrow0< x< 1\)
Đúng 0
Bình luận (0)
a) \(P\left(x\right):"x^2-5x+4=0"\)
\(x^2-5x+4=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=4\end{matrix}\right.\)
Vậy \(x\in\left\{1;4\right\}\) để \(P\left(x\right):"x^2-5x+4=0"\) đúng
b) \(P\left(x\right):"x^2-5x+6=0"\)
\(x^2-5x+6=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=3\end{matrix}\right.\)
Vậy \(x\in\left\{2;3\right\}\) để \(P\left(x\right):"x^2-5x+6=0"\) đúng
c) \(P\left(x\right):"x^2-3x=0"\)
\(x^2-3x=0\)
\(\Leftrightarrow x\left(x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=3\end{matrix}\right.\)
Vậy \(x\in\left\{0;3\right\}\) để \(P\left(x\right):"x^2-3x=0"\) đúng
d) \(P\left(x\right):"\sqrt[]{x}>x"\)
\(\sqrt[]{x}>x\)
\(\Leftrightarrow x-\sqrt[]{x}< 0\)
\(\Leftrightarrow\sqrt[]{x}\left(\sqrt[]{x}-1\right)< 0\)
\(\Leftrightarrow0< x< 1\)
Vậy \(x\in\left(0;1\right)\) để \(P\left(x\right):"\sqrt[]{x}>x"\) đúng
e) \(P\left(x\right):"2x+3< 7"\)
\(2x+3< 7\)
\(\Leftrightarrow2x< 4\)
\(\Leftrightarrow x< 2\)
Vậy \(x\in(-\infty;2)\) để \(P\left(x\right):"2x+3< 7"\) đúng
f) \(P\left(x\right):"x^2+x+1>0"\)
\(x^2+x+1>0\)
\(\Leftrightarrow x^2+x+\dfrac{1}{4}+\dfrac{3}{4}>0\)
\(\Leftrightarrow\left(x+\dfrac{1}{2}\right)^2+\dfrac{3}{4}>0\)
\(\Leftrightarrow\forall x\in R\) để \(P\left(x\right):"x^2+x+1>0"\) đúng
Đúng 0
Bình luận (0)
Cho P = \(\dfrac{2\sqrt{x}-1}{\sqrt{x}-1}\) ( x lớn hơn hoặc bằng 0, x khác 1) Tìm x để P lớn hơn hoặc bằng 1
Để \(P\ge1\) thì \(P-1\ge0\)
\(\Leftrightarrow\dfrac{2\sqrt{x}-1-\sqrt{x}+1}{\sqrt{x}-1}\ge0\)
\(\Leftrightarrow\dfrac{\sqrt{x}}{\sqrt{x}-1}\ge0\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x}=0\\\sqrt{x}-1>0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x>1\end{matrix}\right.\)
Kết hợp ĐKXĐ, ta được: x=0 hoặc x>1
Đúng 0
Bình luận (0)
Gọi a là số thực lớn nhất để bất phương trình
x
2
-
x
+
2
+
a
ln
(
x
2
-
x
+
1
)
≥
0
nghiệm đúng với mọi x. Mệnh đề nào sau đây đúng? A. . B. . C. . D. .
Đọc tiếp
Gọi a là số thực lớn nhất để bất phương trình x 2 - x + 2 + a ln ( x 2 - x + 1 ) ≥ 0 nghiệm đúng với mọi x. Mệnh đề nào sau đây đúng?
A. 
.
B. 
.
C. 
.
D. 
.
Đáp án B
Đặt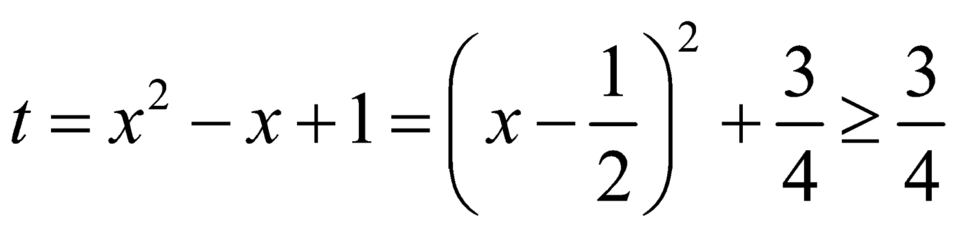 
Ta có:
Đặt 
.
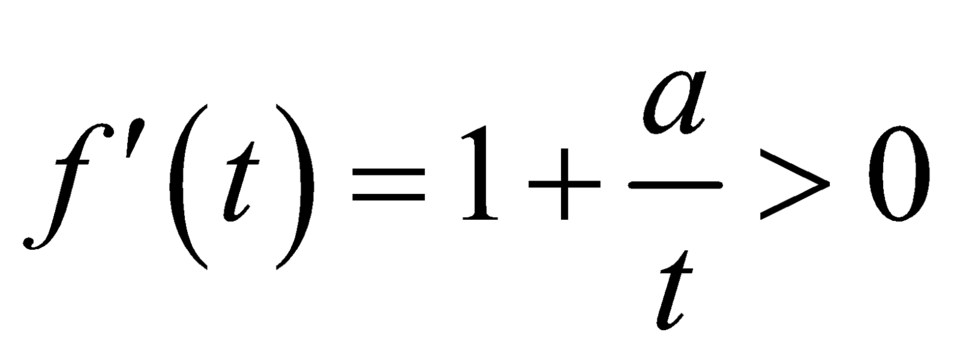
là hàm số đồng biến trên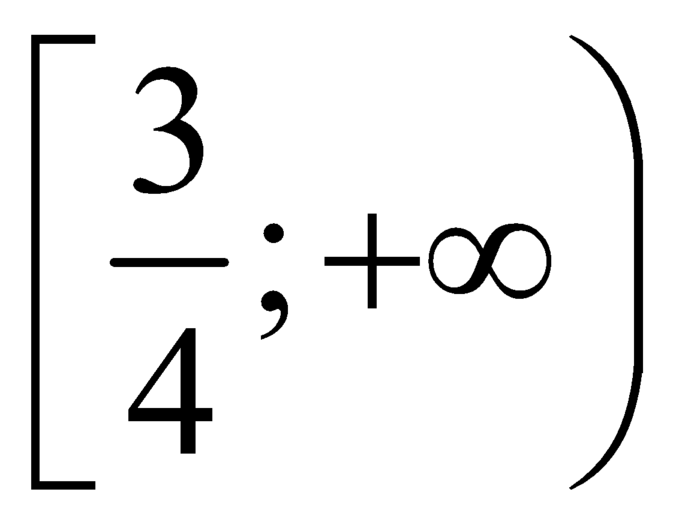 
.
Khi đó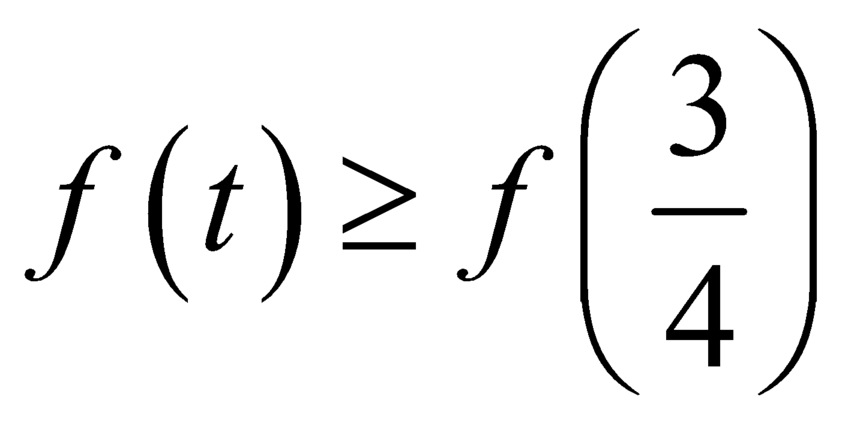 
Đúng 0
Bình luận (0)
1. Mệnh đề nào đúng , giải thích ?
a ) P: ∃ xϵ R, 5x _ 3x 2 ≤ 1
2. Xem mđ đó đúng hay sai
a) P= ∃ x ϵ R: x 2 ≤ 0
b) P = ∀ x ϵ R : x ≤ x 2
c) P = ∀ x ϵ Q : 4x2 - 1 ≠ 0
d) P = ∃ x ϵ R : x2 - x + 7 nhỏ hơn 0
Câu 2:
a: Sai
b: Sai
c: Sai
d: Đúng
Đúng 0
Bình luận (0)
Gọi a là số thực lớn nhất để bất phương trình
x
2
-
x
+
2
+
a
ln
(
x
2
-
x
+
1
)
≥
0
nghiệm đúng với mọi
x
∈
R
. Mệnh đề nào sau đây đúng? A.
a
∈
(
8
;
+
∞
)
B.
a...
Đọc tiếp
Gọi a là số thực lớn nhất để bất phương trình x 2 - x + 2 + a ln ( x 2 - x + 1 ) ≥ 0 nghiệm đúng với mọi x ∈ R . Mệnh đề nào sau đây đúng?
A. a ∈ ( 8 ; + ∞ )
B. a ∈ ( - 6 ; - 5 )
C. a ∈ ( 6 ; 7 )
D. a ∈ ( 2 ; 3 )
a) tìm x để A lớn hơn hoặc bằng 0; A bé hơn 0 biết A=x.(x-2)
b) Tìm x để B lớn hơn 0;B bé hơn hoặc bằng 0 biết B=(x+2) / (3-x)
Tìm hai giá trị x để mệnh đề chứa biến sau thành một mệnh đề đúng và mệnh để sai: a) P(x): 7x2+ 2x- 5= 0 b) P(x): \( {3x+1{} \over 2-x}<0\)
a) \(P\left(x\right)=7x^2+2x-5\)
+) Với x = -1. Ta có: \(P\left(-1\right)=7.\left(-1\right)^2+2.\left(-1\right)-5=0\)
=> \(P\left(x\right)=7x^2+2x-5\) là mệnh đề đúng với x=-1
+) Với x =1 . Ta có: \(P\left(1\right)=7.1^2+2.1-5=4\ne0\)
=> \(P\left(x\right)=7x^2+2x-5\) là mệnh đề sai với x=1
b) Làm tương tự chọn ra hai giá trị
Đúng 0
Bình luận (0)
Gọi a là số thực lớn nhất để bất phương trình
x
2
-
x
+
2
+
a
ln
x
2
-
x
+
1
≥
0
nghiệm đúng với mọi
x
∈
ℝ
. Mệnh đề nào sau đây đúng? A.
a
∈
(
2
;
3...
Đọc tiếp
Gọi a là số thực lớn nhất để bất phương trình x 2 - x + 2 + a ln x 2 - x + 1 ≥ 0 nghiệm đúng với mọi x ∈ ℝ . Mệnh đề nào sau đây đúng?
A. a ∈ ( 2 ; 3 ]
B. a ∈ 8 ; + ∞
C. a ∈ ( 6 ; 7 ]
D. a ∈ ( - 6 ; - 5 ]
Chọn đáp án C
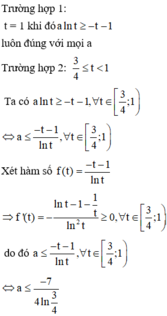
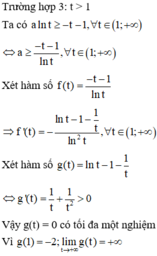
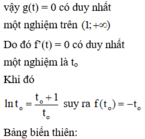
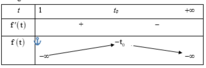
Vậy số thực a thỏa mãn yêu cầu bài toán là: a ∈ ( 6 ; 7 ]
Đúng 0
Bình luận (0)
Gọi a là số thực lớn nhất để bất phương trình
x
2
−
x
−
2
+
a
ln
x
2
−
x
+
1
≥
0
nghiệm đúng với mọi
x
∈
ℝ
.
Mệnh đề nào sau đây đúng? A.
a
∈
6...
Đọc tiếp
Gọi a là số thực lớn nhất để bất phương trình x 2 − x − 2 + a ln x 2 − x + 1 ≥ 0 nghiệm đúng với mọi x ∈ ℝ . Mệnh đề nào sau đây đúng?
A. a ∈ 6 ; 7 .
B. a ∈ 2 ; 3 .
C. a ∈ − 6 ; − 5 .
D. a ∈ 8 ; + ∞
Đáp án A.
Đặt t = x 2 − x + 1 = x − 1 2 2 + 3 4 ≥ 3 4
Khi đó BPT trở thành
f t = t + 1 + a ln t ≥ 0
Ta có: f ' t = + ∞ ; f 3 4 = 3 4 + a ln 3 4
Với a > 0 ⇒ f t đồng biến trên
3 4 ; + ∞ ⇒ f t ≥ 0 ∀ t ∈ 3 4 ; + ∞ ⇔ M i n 3 4 ; + ∞ f t = 7 4 + a
⇔ a ln 3 4 ≥ − 7 4 ⇔ a ≤ − 7 4 ln 3 4 ≈ 6 , 08.
Vì đề bài yêu cầu tìm số thực lớn nhất
nên suy ra a ∈ 6 ; 7 .
Đúng 0
Bình luận (0)