Cho tam giác ABC đều cạnh bằng a, M là trung điểm của BC tính độ dài vecto AM

Những câu hỏi liên quan
Cho tam giác đều ABC có các cạnh bằng 3a, gọi M là trung điểm của BC, I là trung điểm của AM, tính vecto AC x BI
Xem chi tiết
Lời giải:
\(\overrightarrow{AC}.\overrightarrow{BI}=(\overrightarrow{AM}+\overrightarrow{MC})(\overrightarrow{BM}+\overrightarrow{MI})\)
\(=\overrightarrow{AM}.\overrightarrow{BM}+\overrightarrow{AM}.\overrightarrow{MI}+\overrightarrow{MC}.\overrightarrow{BM}+\overrightarrow{MC}.\overrightarrow{MI}\)
\(=\overrightarrow{AM}.\overrightarrow{MI}+\overrightarrow{MC}.\overrightarrow{BM}\)
\(=\overrightarrow{AM}.\frac{-\overrightarrow{AM}}{2}+\frac{\overrightarrow{BC}}{2}.\overrightarrow{BC}=\frac{BC^2-AM^2}{2}\)
\(=\frac{BC^2-(\frac{\sqrt{3}}{2}BC)^2}{2}=\frac{BC^2}{8}=\frac{9a^2}{8}\)
Đúng 0
Bình luận (0)
Cho tam giác đều abc có cạnh ab=4cm, gọi M là trung điểm cạnh bc .tính độ dài vecto bm-ba.
\(=\dfrac{4\sqrt{3}}{2}=2\sqrt{3}\)
Đúng 0
Bình luận (0)
cho tam giác đều ABC cạnh a. M là trung điểm AC. Tính độ dài vecto BA+ vecto BM
ΔABC đều có BM là đường trung tuyến
nên BM là phân giác của góc ABC và BM\(\perp\)AC
BM là phân giác của góc ABC
=>\(\widehat{ABM}=\widehat{CBM}=\dfrac{\widehat{ABC}}{2}=30^0\)
M là trung điểm của AC
=>\(AM=MC=\dfrac{AC}{2}=\dfrac{a}{2}\)
ΔAMB vuông tại M
=>\(AM^2+BM^2=AB^2\)
=>\(BM^2=AB^2-AM^2=a^2-\left(0,5a\right)^2=0,75a^2\)
=>\(BM=\dfrac{a\sqrt{3}}{2}\)
Gọi K là trung điểm của AM
=>\(KA=KM=\dfrac{AM}{2}=0,25a\)
ΔBMK vuông tại M
=>\(BM^2+MK^2=BK^2\)
=>\(BK^2=\left(0,25a\right)^2+\left(\dfrac{a\sqrt{3}}{2}\right)^2=\dfrac{13}{16}a^2\)
=>\(BK=\dfrac{a\sqrt{13}}{4}\)
Xét ΔBAM có BK là đường trung tuyến
nên \(\overrightarrow{BA}+\overrightarrow{BM}=2\cdot\overrightarrow{BK}\)
=>\(\left|\overrightarrow{BA}+\overrightarrow{BM}\right|=2\cdot BK=2\cdot\dfrac{a\sqrt{13}}{4}=\dfrac{a\sqrt{13}}{2}\)
Đúng 1
Bình luận (0)
cho tam giác ABC cân tại A, M là trung điểm của BC. CMR: a, tam giác AMB= tam giác AMC. b, tính độ dài AM biết AB=10cm; BC=12cm c, kẻ đường trung tuyến CE cắt AM tại D. gọi I là điểm cách đều 3 cạnh của tam giác ABC. CMR: I;D;M thẳng hàng.
a: Xet ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
Do đó: ΔAMB=ΔAMC
b: Ta có: ΔABC cân tại A
mà AM là trung tuyến
nên AM là đường cao
BC=12cm nên BM=6cm
=>AM=8(cm)
c: I cách đều ba cạnh nên I là giao điểm của ba đường phân giác
=>AI là phân giác của góc BAC
mà AM là phân giác của góc BC
nên A,I,M thẳng hàng
Đúng 3
Bình luận (0)
Cho tam giác ABC vuông tại A có AB = 3, AC = 4. Gọi M là một điểm trên cạnh BC và D là chân đường phân giác trong góc A. Tính độ dài vecto MD khi độ dài vecto AM nhỏ nhất
cho tam giác đều ABC có cạnh bằng a ,H là trung điểm của BC.Vecto CH + vecto CH có độ dài là:
\(\left|\overrightarrow{CH}+\overrightarrow{CH}\right|=a\)
Đúng 0
Bình luận (0)
Cho tam giác ABC lấy điểm M trên cạnh BC sao cho BM = 3MC. Gọi I là trung điểm của BC va G la trọng tâm của tam giac ABC. Tính vecto AM theo vecto AG va vecto BC
Cho tam giác đều ABC có cạnh bằng 6cm. Một điểm M nằm trên cạnh BC sao cho BM = 2cm.
a, Tính độ dài của đoạn thẳng AM và tính côsin của góc BAM ;
b, Tính bán kính đường tròn ngoại tiếp tam giác ABM;
c, Tính độ dài đường trung tuyến vẽ từ đỉnh C của tam giác ACM;
d, Tính diện tích tam giác ABM.
a) Do tam giác ABC là tam giác đều nên 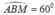 .
.
Theo định lý côsin trong tam giác ABM ta có:

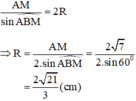
b) Theo định lý sin trong tam giác ABM ta có:
c) Ta có: BM + MC = BC nên MC = BC – BM = 6 - 2 = 4 cm.
Gọi D là trung điểm AM.
Áp dụng công thức độ dài đường trung tuyến trong tam giác ta có:
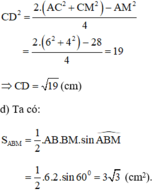
Đúng 0
Bình luận (0)
CHo tam giác ABC đều có cạnh là 6. Gọi M, N, P lần lượt là ttrung điểm của AB, AC, BC.
â. kể tên các vectơ bằng vectơ MN
b. tính độ dài vecto MNnhaan độ dài vecto AP
c. hạ PH vuông góc với AC tại H. tính độ dài vecto PH














