Bạn tự vẽ hình nha 

1. Xét tam giác EBH có: BE=BH (gt) -> tan giác EBH cân tại B -> góc BEH = góc BHE

Ta lại có góc ABH = góc BEH + góc BHE (góc ngoài của tam giác EBH); Mà góc BEH = góc BHE (cmt) -> góc ABH = 2 góc BEH; Mà góc ABH = 2 góc ACB (gt)-> góc BEH = góc ACB ( đpcm)

2. Ta có: góc BHE = góc DHC (2 góc đối đỉnh); Mà góc BHE = góc BEH (cmt) và góc BEH = góc ACB (cmt) => góc DHC = góc ACB -> tam giác DHC cân tại D -> DH = DC ( 2 cạnh tương ứng)

Ta có: tam giác AHC vuông tại H -> góc HAC +góc ACB = 90 độ (2 góc ở đáy tam giác vuông ); Mà  góc AHD + góc DHC = 90 độ và góc ACB = góc DHC (cmt) -> góc HAC = góc AHD -> tam giác AHD cân tại D => DA = DH (2 cạnh tương ứng ) 

Vậy DH=DC=DA

3. Ta có tam giác ABB' có: BH = B'H ( H là trung điểm BB') -> AH là đường trung tuyến lại vừa là đường cao -> tam giác ABB' cân tại A -> góc ABH = góc AB'H (2 góc ở đáy)

Xét tam giác AB'C có: góc AB'H = góc B'AC + góc ACB' (góc ngoài); Mà góc ABH = góc AB'H (cmt) -> góc ABH = góc B'AC + góc ACB ; Mà góc ABH = 2 góc ACB'

-> góc B'AC = góc ACB' => tam giác AB'C cân tại B'

4. Bạn vẽ lại hình nha: giả sử tam giác ABC vuông tại A

Xét tam giác ADE và tam giác ABC có: góc A chung và góc BEH = góc ACB (cmt) -> hai tam giác đồng dạng theo trường hợp (g.g) -> góc ADE = góc ABC (2 góc tương ứng) (1) 

Ta có : góc HAD = 90 độ - góc C ( tam giác HAC vuông tại H); Mà góc ABC = 90 độ - góc C ( tam giác ABC vuông tại A) -> góc HAD = góc ABC (2)

Từ (1) và (2) -> góc ADE = góc HAD; Mà góc HAD = góc AHD nên suy ra tam giác AHD đều 

Xét tam giác ADE và tâm giác HAC có: góc EAD = góc CHA = 90 độ (gt); góc ADE = góc HAC (cmt); AD = AH (tam giác AHD đều) => tam giác ADE = tam giác HAC theo trường hợp (g.c.g)

=> DE = AC (2 cạnh tương ứng) => DE² = AC² ; Mà AC² = BC² - AB² (định lí Py-ta-go trong tam giác ABC) => DE² = BC² - AB² (đpcm) 

Học tốt nhé 🙋‍♀️🙋‍♀️🙋‍♀️💗💗💗

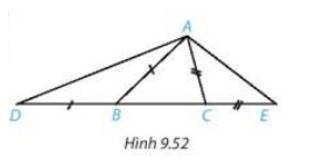
a)

\(AB > AC \Rightarrow \widehat {ABC} < \widehat {ACB}\)( quan hệ giữa góc và cạnh đối diện trong tam giác ABC)

\(\begin{array}{l} \Rightarrow {180^0} - \widehat {ABD} < {180^0} - \widehat {ACE}\\ \Rightarrow \widehat {ABD} > \widehat {ACE}\end{array}\)

Vì BD= BA nên tam giác ABD cân tại B \( \Rightarrow \widehat {ABD} = {180^0} - 2\widehat {ADB}\)

Vì CE = CA nên tam giác ACE cân tại C \( \Rightarrow \widehat {ACE} = {180^0} - 2\widehat {AEC}\)

\(\begin{array}{*{20}{l}}{ \Rightarrow {{180}^0} - 2\widehat {ADB} > {{180}^0} - 2\widehat {AEC}}\\{ \Rightarrow \widehat {ADB} < \widehat {AEC}}\\{Hay{\mkern 1mu} \widehat {ADE} < \widehat {AED}}\end{array}\)

b) Xét tam giác ADE ta có : \(\widehat {ADB} < \widehat {AEC}\)

\( \Rightarrow AD > AE\)(Quan hệ giữa cạnh và góc đối diện trong tam giác). 

Tham khảo:

a) Vì tam giác ABC vuông tại A nên \(\widehat{A}=90^0; \widehat{B}+\widehat{C}=90^0\)

Vì \(\widehat B > {45^o} \Rightarrow \widehat C < {45^o} \Rightarrow \widehat A > \widehat B > \widehat C \Rightarrow BC > AC > AB\)

b) Vì \(\widehat {BKC}\) là góc ngoài tại đỉnh K của tam giác ABK nên \(\widehat {BKC}>(\widehat {BAK}=90^0\)

Xét tam giác BCK, ta có :

\(\widehat {BKC} > {90^o} > \widehat {BCK}\)

\( \Rightarrow BC > BK\) ( quan hệ giữa góc và cạnh đối diện trong tam giác)

ddđds

a: Xét ΔABC có AC>AB

mà HC,HB lần lượt là hình chiếu của AC,AB trên BC

nên HC>HB

b: Xét ΔDBC có HB<HC

mà HB,HC lần lượt là hình chiếu của DB,DC trên BC

nên DB<DC

a) vì góc A lớn nhất nên góc A có thể là góc vuông, góc tù hoặc góc nhọn.

+trường hợp A là góc vuông và góc tù thì góc B và C ko thể lớn hơn hoặc bằng 90 độ. do đó góc B và C là góc nhọn

+ trường hợp góc A là góc nhọn thì góc B và góc C cx bé hơn 90 độ vì góc A>góc B> góc C.

a) Ta có: góc A> góc B> góc C

\(\Rightarrow\) góc B và góc C là góc nhọn

Tức quá , lag chết đi đc

b) Xét tam giác ABC có góc B > góc C

=> AC>AB (...........)

=> HC>HB ( quan hệ đường xiên hình chiếu )

=> OC>OB ( quan hệ đường xiên hình chiếu )

c) Xét tam giác OHC vuông tại H có :

góc HOC + góc HCO = 90 độ

=> góc HOC là góc nhọn

Ta có : góc HOC + góc HOD = 180 độ ( kề bù )

mà góc HOC là góc nhọn

=> góc HOD là góc tù

Xét tam giác OHD có góc HOD là góc tù

=> HD>OD ( quan hệ giữa góc và cạnh trong một tam giác)