a: Gọi O là giao của AC và BD

ABCD là hình bình hành

=>AC cắt BD tại trung điểm của mỗi đường

=>O là trung điểm chung của AC và BD

Xét tứ giác AECG có

AE//CG

AE=CG

Do đó: AECG là hình bình hành

=>AG//CE và AG=CE

Xét tứ giác AHCF có

AH//CF

AH=CF

Do đó: AHCF là hình bình hành

=>AF//CH và AF=CH

Xét ΔANB có

E là trung điểm của AB

EM//AN

Do đó: M là trung điểm của BN

=>BM=MN

Xét ΔDMC có

G là trung điểm của DC

GN//MC

Do đó: N là trung điểm của DM

=>DN=MN=MB=1/3DB

DN=1/3DB

DO=1/2DB

Do đó: \(\dfrac{DN}{DO}=\dfrac{1}{3}:\dfrac{1}{2}=\dfrac{2}{3}\)

Xét ΔADC có

DO là trung tuyến

DN=2/3DO

Do đó: N là trọng tâm

=>A,N,G thẳng hàng và C,N,H thẳng hàng

Xét ΔABC có

BO là trung tuyến

BM=2/3BO

Do đó: M là trọng tâm

=>A,M,F thẳng hàng và C,M,E thẳng hàng

Xét ΔEBM và ΔGDN có

EB=GD

\(\widehat{EBM}=\widehat{GDN}\)

BM=DN

Do đó: ΔEBM=ΔGDN

=>EM=GN

Xét tứ giác EMGN có

EM//GN

EM=GN

Do đó: EMGN là hình bình hành

b: Để EMGN là hình chữ nhật thì EG=NM

=>\(AD=\dfrac{BD}{3}\)

Xét ΔBAC có

E là trung điểm của BA(gt)

F là trung điểm của BC(gt)

Do đó: FE là đường trung bình của ΔBAC(Định nghĩa đường trung bình của tam giác)

⇒FE//AC và \(FE=\dfrac{AC}{2}\)(Định lí 2 về đường trung bình của tam giác)(1)

Xét ΔDAC có

H là trung điểm của AD(gt)

G là trung điểm của DC(gt)

Do đó: HG là đường trung bình của ΔDAC(Định nghĩa đường trung bình của tam giác)

⇒HG//AC và \(HG=\dfrac{AC}{2}\)(Định lí 2 về đường trung bình của tam giác)(2)

Từ (1) và (2) suy ra EF//HG và EF=HG

Xét tứ giác EFGH có

EF//HG(cmt)

EF=HG(cmt)

Do đó: EFGH là hình bình hành(Dấu hiệu nhận biết hình bình hành)

Xét ΔBCD có 

F là trung điểm của BC(gt)

G là trung điểm của CD(gt)

Do đó: FG là đường trung bình của ΔBCD(Định nghĩa đường trung bình của tam giác)

⇒FG//BD và \(FG=\dfrac{BD}{2}\)(Định lí 2 về đường trung bình của tam giác)(3)

Ta có: AC=BD(gt)

nên \(\dfrac{AC}{2}=\dfrac{BD}{2}\)(4)

Từ (2), (3) và (4) suy ra HG=FG

Hình bình hành EFGH có HG=FG(cmt)

nên EFGH là hình thoi(Dấu hiệu nhận biết hình thoi)

⇒\(S_{EFGH}=\dfrac{1}{2}\cdot EG\cdot HF=\dfrac{1}{2}\cdot5\cdot4=10cm^2\)

Xét ΔACB có

E là trung điểm của AB

F là trung điểm của BC

Do đó: EF là đường trung bình của ΔACB

Suy ra: EF//AC và \(EF=\dfrac{AC}{2}\left(1\right)\)

Xét ΔADC có 

H là trung điểm của AD

G là trung điểm của CD

Do đó: HG là đường trung bình của ΔADC

Suy ra: HG//AC và \(HG=\dfrac{AC}{2}\left(2\right)\)

Từ (1) và (2) suy ra EF//HG và EF=HG

Xét ΔABD có 

E là trung điểm của AB

H là trung điểm của AD

Do đó: EH là đường trung bình của ΔABD

Suy ra: \(EH=\dfrac{BD}{2}=\dfrac{AC}{2}\left(3\right)\)

Từ (1) và (3) suy ra EF=EH

Xét tứ giác EHGF có 

EF//GH

EF=GH

Do đó: EHGF là hình bình hành

mà EF=EH

nên EHGF là hình thoi

+ E là trung điểm AB, F là trung điểm BC

⇒ EF là đường trung bình của tam giác ABC

⇒ EF // AC và EF = AC/2

+ H là trung điểm AD, G là trung điểm CD

⇒ HG là đường trung bình của tam giác ACD

⇒ HG // AC và HG = AC/2.

+ Ta có:

EF //AC, HG//AC ⇒ EF // HG.

EF = AC/2; HG = AC/2 ⇒ EF = HG

⇒ tứ giác EFGH là hình bình hành.

có thể giúp mk trả lời phần a ko ạ

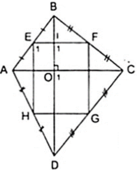
Tứ giác EFGH là hình chữ nhật.

Giải thích: Theo giả thiết ta có EF, GH lần lượt là đường trung bình của tam giác Δ ABC,Δ ADC

Áp dụng định lí đường trung bình vào hai tam giác ta được

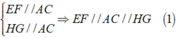
Chứng minh tương tự: EH//FG//BD      ( 2 )

Từ ( 1 ) và ( 2 ), tứ giác EFGH có hai cặp cạnh đối song song nên tứ giác EFGH là hình bình hành.

Gọi O là giao điểm của AC và BD, I là giao điểm của EF với BD.

Áp dụng tính chất của các góc đồng vị vào các đường thẳng song song ở trên và giả thiết nên ta có:

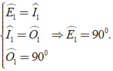
Hình bình hành EFGH có một góc vuông nên EFGH là hình chữ nhật. 

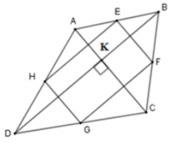
Vì E, F, G, H lần lượt là trung điểm các cạnh AB,BC,CD,DA nên EF, FG, GH, HE lần lượt là đường trung bình của tam giác ABC, BCD, ADC, ADB nên 

EF//HG (cùng song song với AC)

HE//FG (cùng song song với BD)

Suy ra tứ giác EFGH là hình bình hành

Mà  A C ⊥ B D (gt)   ⇒ E F ⊥ F G

Suy ra EFGH là hình chữ nhật

Do đó  S E F G H = H E . E F mà  E F = 1 2 A C ;  H E = 1 2 B D (tính chất đường trung bình)