Cho x\(\ge\)3; y\(\ge2\); z\(\ge\)1. Chứng minh rằng:
\(\dfrac{xy\sqrt{x-1}+zx\sqrt{y-2}+yz\sqrt{z-3}}{xyz}\le\dfrac{1}{2}+\dfrac{\sqrt{2}}{4}+\dfrac{\sqrt{3}}{6}\)
Những câu hỏi liên quan
Cho x \(\ge\)0.Chứng minh \(x^3\)+4\(\ge\)3\(x^2\)
Cho x \(\ge\)3.Chứng minh x +\(\frac{1}{x}\)\(\ge\)\(\frac{10}{3}\)
Áp dụng BĐT cosi:
`x+9/x>=6`
`=>x+1/x`
`=x+9/x-8/x>=6-8/x`
Vì `x>=3=>8/x<=8/3`
`=>6-8/x>=6-8/3=10/3`
Dấu "=" `<=>x=3`
Đúng 0
Bình luận (0)
16 tháng 6 2021 lúc 10:00
Cho A= \(\dfrac{\sqrt{x}}{\sqrt{x}+3}\) với ĐK x \(\ge\)0
B= \(\dfrac{2\sqrt{x}}{\sqrt{x}+3}\) với ĐK x\(\ge\)0
Tính M biết M= A+B
\(M=A+B=\dfrac{\sqrt{x}}{\sqrt{x}+3}+\dfrac{2\sqrt{x}}{\sqrt{x}+3}=\dfrac{\sqrt{x}+2\sqrt{x}}{\sqrt{x}+3}=\dfrac{3\sqrt{x}}{\sqrt{x}+3}\left(x\ge0\right)\)
Đúng 1
Bình luận (0)
`M=A+B`
`=sqrtx/(sqrtx+3)+(2sqrtx)/(sqrtx+3)`
`=(sqrtx+2sqrtx)/(sqrtx+3)`
`=(3sqrtx)/(sqrtx+3)`
Đúng 1
Bình luận (0)
Với \(x\ge0\), ta có:
\(M=A+B=\dfrac{\sqrt{x}}{\sqrt{x}+3}+\dfrac{2\sqrt{x}}{\sqrt{x}+3}\) \(=\dfrac{3\sqrt{x}}{\sqrt{x}+3}\) \(=\dfrac{3\sqrt{x}\left(\sqrt{x}-3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\) \(=\dfrac{3x-9\sqrt{x}}{x-9}\)
#Cho mình sửa lại chút nhé! Nãy lag tí :)))
Đúng 2
Bình luận (0)
Cho \(x\ge y\ge z\ge0\). Chứng minh BĐT sau
a/ \(xy^3+yz^3+zx^3\ge xz^3+zy^3+yx^3\)
b/ \(\dfrac{x^2y}{z}+\dfrac{y^2z}{x}+\dfrac{z^2x}{y}\ge\dfrac{x^2z}{y}+\dfrac{y^2x}{z}+\dfrac{z^2y}{x}\)
a) BĐT \(\Leftrightarrow\left(x-y\right)\left(y-z\right)\left(z-x\right)\left(x+y+z\right)\ge0\)
suy ra sai đề
b) BĐT \(\Leftrightarrow\dfrac{\left(x-y\right)\left(y-z\right)\left(x-z\right)\left(xy+yz+xz\right)}{xyz}\ge0\) ( đúng vì \(x\ge y\ge z>0\))
Đúng 0
Bình luận (0)
Cho x,y là các số dương thõa \(x^2+y^3\ge x^3+y^4\). CMR:
a)\(x^2+y^2\ge x^3+y^3\) b)\(x+y^2\ge x^2+y^3\)
Ta có:\(\left(y^2-y\right)+2\ge0\Rightarrow2y^3\le y^4+y^2\\ \Rightarrow\left(x^3+y^2\right)+\left(x^2+y^3\right)\le\left(x^2+y^2\right)+\left(y^4+x^3\right)\)
Mà:\(x^3+y^4\le x^2+y^3\)
\(\Rightarrow x^3+y^3\le x^2+y^2\)
Đúng 0
Bình luận (0)
Cho x,y,z>-1 thỏa mãn
\(x^3+y^3+z^3\ge x^2+y^2+z^2\)
Chứng minh rằng
\(x^5+y^5+z^5\ge x^2+y^2+z^2\)
cho các số thực dương x,y,x thỏa mãn xy ≥ 1 và z ≥1
Chứng minh bất đẳng thức \(\frac{x}{y+1}+\frac{y}{x+1}+\frac{z^3+2}{3\left(xy+1\right)}\ge\frac{3}{2}\)
a)Cho các số x,y,z ge1.CMR: frac{1}{1+x}+frac{1}{1+y}+frac{1}{1+z}gefrac{3}{1+sqrt[3]{xyz}}.b) Cho x,y,z ge0 và xle1;yle1;zle1chứng minh:frac{1}{1+x^2}+frac{1}{1+y^2}+frac{1}{1+z^2}lefrac{3}{1+xyz}c)Cho a + bge2.CMR: a^3+b^3le a^4+b^4d)Cho a2+b2gefrac{1}{4}.CMR:a^4+b^4gefrac{1}{32}
Đọc tiếp
a)Cho các số x,y,z \(\ge\)1.CMR: \(\frac{1}{1+x}+\frac{1}{1+y}+\frac{1}{1+z}\ge\frac{3}{1+\sqrt[3]{xyz}}\).
b) Cho x,y,z \(\ge\)0 và x\(\le1;y\le1;z\le1\)chứng minh:
\(\frac{1}{1+x^2}+\frac{1}{1+y^2}+\frac{1}{1+z^2}\le\frac{3}{1+xyz}\)
c)Cho a + b\(\ge\)2.CMR: \(a^3+b^3\le a^4+b^4\)
d)Cho a2+b2\(\ge\frac{1}{4}.CMR:a^4+b^4\ge\frac{1}{32}\)
\(x,y,z\ge1\)nên ta có bổ đề: \(\frac{1}{a^2+1}+\frac{1}{b^2+1}\ge\frac{2}{ab+1}\)
ÁP dụng: \(\frac{1}{x+1}+\frac{1}{y+1}+\frac{1}{z+1}+\frac{1}{1+\sqrt[3]{xyz}}\ge\frac{2}{1+\sqrt{xy}}+\frac{2}{1+\sqrt{\sqrt[3]{xyz^4}}}\)
\(\ge\frac{4}{1+\sqrt[4]{\sqrt[3]{x^4y^4z^4}}}=\frac{4}{1+\sqrt[3]{xyz}}\)
\(\Rightarrow\frac{1}{1+x}+\frac{1}{1+y}+\frac{1}{1+z}\ge\frac{3}{1+\sqrt[3]{xyz}}\)
Dấu = xảy ra \(x=y=z\)hoặc x=y,xz=1 và các hoán vị
Đúng 0
Bình luận (0)
trc giờ mấy bài này tui toàn quy đồng thôi, may có cách này =))
Đúng 0
Bình luận (0)
vì \(x,y,z\in\left[0;1\right]\)nên \(x^2\ge x^3;y^2\ge y^3;z^2\ge z^3\)
\(VT\le\frac{1}{1+x^3}+\frac{1}{1+y^3}+\frac{1}{1+z^3}\le\frac{3}{1+xyz}\)đúng theo BĐT câu a vì \(x,y,z\le1\)nên BĐT đổi chiều
Dấu = xảy ra:(x,y,z)=(0;0;0);(1;1;1) ;(1;0;1);(0;1;1);(1;1;0)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Miền không bị gạch ở mỗi Hình 12a, 12b là miền nghiệm của hệ bất phương trình nào cho ở dưới đây?a) left{ begin{array}{l}x + y le 2x ge - 3y ge - 1end{array} right.b) left{ begin{array}{l}y le xx le 0y ge - 3end{array} right.c) left{ begin{array}{l}y ge - x + 1x le 2y le 1end{array} right.
Đọc tiếp
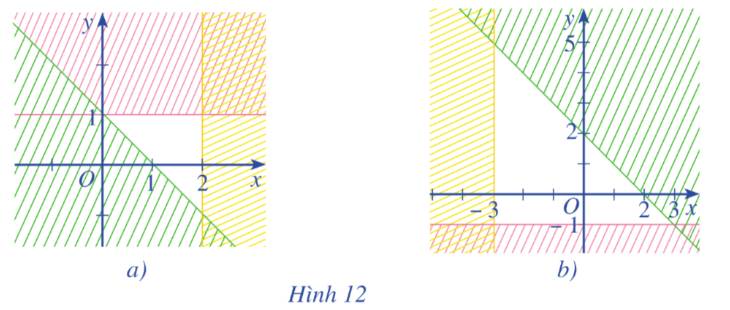
Miền không bị gạch ở mỗi Hình 12a, 12b là miền nghiệm của hệ bất phương trình nào cho ở dưới đây?
a) \(\left\{ \begin{array}{l}x + y \le 2\\x \ge - 3\\y \ge - 1\end{array} \right.\)
b) \(\left\{ \begin{array}{l}y \le x\\x \le 0\\y \ge - 3\end{array} \right.\)
c) \(\left\{ \begin{array}{l}y \ge - x + 1\\x \le 2\\y \le 1\end{array} \right.\)
Hình 12a
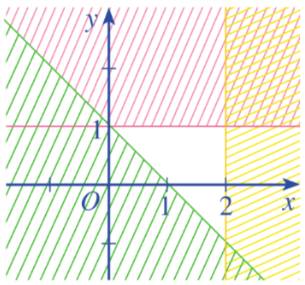
Ta thấy các đường thẳng trên hình là \(y = 1;x = 2;y = - x + 1\)
Từ các phương trình trên thì ta chọn luôn là câu c mà không cần xét tiếp.
Hình 12b.
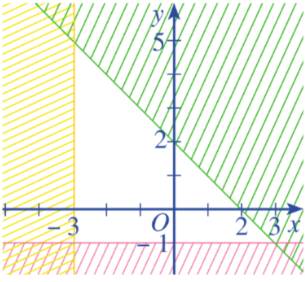
Ta thấy các đường thẳng trên hình là \(y = - 1;x = - 3;x + y = - 2\)
Từ các phương trình trên thì ta chọn luôn là câu a mà không cần xét tiếp
Đúng 0
Bình luận (0)
Cho x,y là các số dương thỏa \(x^2+y^3\) ≥ \(x^3+y^4\). CMR
a) \(x^2+y^2\) ≥ \(x^3+y^3\)
b) \(x+y^2\) ≥ \(x^2+y^3\)