cho △ABC . Gọi AH ,BL , CL lần lượt là 3 đường cao của △ABC . Chứng minh rằng : AK.BL.CH = AB.BC.CA.cosA.cosB.cosC
Những câu hỏi liên quan
Gọi AM, BN, CL lần lượt là ba đường cao của tam giác ABC. Chứng minh: AN.BL.CM = AB.BC.CA.cosA.cosB.cosC
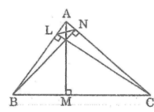
ABN vuông tại N nên AN = AB.cosB (1)
∆ BCL vuông tại L nên BL = BC.cosB (2)
∆ ACM vuông tại M nên CM = AC.cosC (3)
Từ (1), (2) và (3) suy ra: AN.BL.CM = AB.BC.CA. cosA cosB cosC
Đúng 0
Bình luận (0)
Cho tam giác ABC. GoijAH, BK, CL lần lượt là ba đường cao của tgiac ABC. CMR: AK.BL.CH = AB.BC.AC.cosA.cosB.cosC
21 tháng 7 2017 lúc 21:53
Cho tam giác nhọn ABC không đều. Kẻ đường cao AH, trung tuyến BM và đường phân giác CL của góc ACB. Trung tuyến BM cắt AH và CL lần lượt tại P, Q. CL cắt AH ở R. Chứng minh rằng tam giác PQR không phải là tam giác đều.
Cho tam giác ABC và đường cao AH. Gọi I, K lần lượt là hình chiếu của H trên AB, AC
Cho tam giác ABC và đường cao AH. Gọi I, K lần lượt là hình chiếu của H trên AB, AC.
a) Chứng minh ED // IK
Xem chi tiết
a) Chứng minh ED // IK
Cho tam giác ABC vuông tại A , đường cao AH . Gọi M,N lần lượt là hình chiếu của H lên AB, AC . Chứng minh rằng :
a) AM.AB=AN.AC
b) MB/NC=(AB/AC)^3
c) BC.MB.NC=AH^3
Cho tam giác ABC vuông tại A, đường cao AH.
Gọi P, Q lần lượt là trung điểm của BH và AH. Chứng minh rằng: r ABP ∽rCAQ
Gọi AM, BN, CL lần lượt là ba đường cao của tam giác ABC. Chứng minh: Tam giác ANL và tam giác ABC đồng dạng
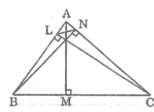
a. Xét hai tam giác BNA và CLA, ta có:
∠ BNA = ∠ CLA = 90 °
góc A chung
Suy ra ∆ BNA đồng dạng ∆ CLA (g.g)
Suy ra: AL/AN = AC/AB ⇒ AL/AC = AN/AB
Xét hai tam giác ABC và ANL, ta có:
AL/AC = AN/AB
góc A chung
Suy ra ∆ ABC đồng dạng ∆ ANL (c.g.c)
Đúng 0
Bình luận (0)
Cho tam giác ABC. Hai đường cao BE, CF cắt nhau tại H. Gọi M và O lần lượt là trung điểm của AH, BC. Chứng minh rằng
a, AFHE là tứ giác nội tiếp
b, OE là tiếp tuyến của đường tròn đường kính AH
c, OE cắt AH tại S. Chứng minh rằng SE2=SH.SA
Ai giúp em nhanh bài tập này được không ạ?
Đúng 0
Bình luận (0)
1 tháng 8 2023 lúc 20:25
Cho tam giác ABC vuông tại A, đường cao AH. Gọi E, F lần lượt là hình chiếu của H lên AB, AC.
a) Chứng minh: AE.AB = AF.AC và \(\widehat{AEF}=\widehat{ABC}\)
b) Đường trung tuyến AI của tam giác ABC cắt EF tại K. Chứng minh rằng \(cos^2B.sinB=\dfrac{KF}{BC}\)
.Ta có :
AH⊥BC,HE⊥AB→\(\widehat{AEH}=\widehat{AHB}\)
=> \(\Delta AEH\approx\Delta AHB\)(g.g)
=>\(\dfrac{AE}{AH}=\dfrac{AH}{AB}\)
=>AH\(^2\)=AE.AB
Lam tuong tu ta dc AH\(^2\)=AF.AC
=> AE.AB=AF.AC
Đúng 0
Bình luận (1)
a: ΔAHB vuông tại H có HE là đường cao
nên AE*AB=AH^2
ΔAHC vuông tại H có HF là đường cao
nen AF*AC=AH^2
=>AE*AB=AF*AC
=>AE/AC=AF/AB
=>ΔAEF đồng dạng với ΔACB
Đúng 0
Bình luận (0)